
Noncentral chi distribution
Encyclopedia
In probability theory
and statistics
, the noncentral chi distribution is a generalization of the chi distribution. If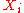 are k independent, normally distributed random variables with means
are k independent, normally distributed random variables with means 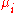 and variances
and variances 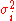 , then the statistic
, then the statistic

is distributed according to the noncentral chi distribution. The noncentral chi distribution has two parameters: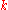 which specifies the number of degrees of freedom
which specifies the number of degrees of freedom
(i.e. the number of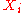 ), and
), and 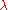 which is related to the mean of the random variables
which is related to the mean of the random variables  by:
by:

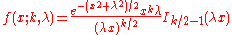
where is a modified Bessel function
is a modified Bessel function
of the first kind.
The first few raw moments
are:
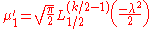
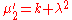
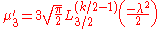

where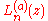 is the generalized Laguerre polynomial. Note that the 2nth moment is the same as the nth moment of the noncentral chi-squared distribution with
is the generalized Laguerre polynomial. Note that the 2nth moment is the same as the nth moment of the noncentral chi-squared distribution with 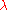 being replaced by
being replaced by 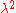 .
.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
and statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the noncentral chi distribution is a generalization of the chi distribution. If
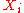 are k independent, normally distributed random variables with means
are k independent, normally distributed random variables with means 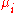 and variances
and variances 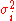 , then the statistic
, then the statistic
is distributed according to the noncentral chi distribution. The noncentral chi distribution has two parameters:
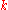 which specifies the number of degrees of freedom
which specifies the number of degrees of freedomDegrees of freedom (statistics)
In statistics, the number of degrees of freedom is the number of values in the final calculation of a statistic that are free to vary.Estimates of statistical parameters can be based upon different amounts of information or data. The number of independent pieces of information that go into the...
(i.e. the number of
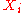 ), and
), and 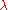 which is related to the mean of the random variables
which is related to the mean of the random variables  by:
by:
Properties
The probability density function is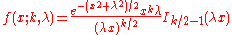
where
 is a modified Bessel function
is a modified Bessel functionBessel function
In mathematics, Bessel functions, first defined by the mathematician Daniel Bernoulli and generalized by Friedrich Bessel, are canonical solutions y of Bessel's differential equation:...
of the first kind.
The first few raw moments
Moment (mathematics)
In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...
are:
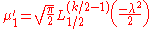
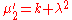
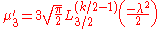

where
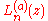 is the generalized Laguerre polynomial. Note that the 2nth moment is the same as the nth moment of the noncentral chi-squared distribution with
is the generalized Laguerre polynomial. Note that the 2nth moment is the same as the nth moment of the noncentral chi-squared distribution with 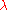 being replaced by
being replaced by 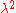 .
.Related distributions
- If
 is a random variable with the non-central chi distribution, the random variable
is a random variable with the non-central chi distribution, the random variable 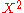 will have the noncentral chi-squared distribution. Other related distributions may be seen there.
will have the noncentral chi-squared distribution. Other related distributions may be seen there.
- If
 is chi distributed:
is chi distributed: 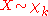 then
then  is also non-central chi distributed:
is also non-central chi distributed: 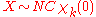 . In other words, the chi distribution is a special case of the non-central chi distribution (i.e., with a non-centrality parameter of zero).
. In other words, the chi distribution is a special case of the non-central chi distribution (i.e., with a non-centrality parameter of zero).
- A noncentral chi distribution with 2 degrees of freedom is equivalent to a Rice distributionRice distributionIn probability theory, the Rice distribution or Rician distribution is the probability distribution of the absolute value of a circular bivariate normal random variable with potentially non-zero mean. It was named after Stephen O...
with .
.
- If X follows a noncentral chi distribution with 1 degree of freedom and noncentrality parameter λ, then σX follows a folded normal distributionFolded Normal DistributionThe folded normal distribution is a probability distribution related to the normal distribution. Given a normally distributed random variable X with mean μ and variance σ2, the random variable Y = |X| has a folded normal distribution. Such a case may be encountered if only the magnitude of some...
whose parameters are equal to σλ and σ2 for any value of σ.

