
Extended negative binomial distribution
Encyclopedia
In probability
and statistics
the extended negative binomial distribution is a discrete probability distribution extending the negative binomial distribution
. It is a truncated
version of the negative binomial distribution for which estimation methods have been studied.
In the context of actuarial science
, the distribution appeared in its general form in a paper by K. Hess, A. Liewald and K.D. Schmidt when they characterized all distributions for which the extended Panjer recursion
works. For the case m = 1, the distribution was already discussed by Willmot and put into a parametrized family with the logarithmic distribution and the negative binomial distribution by H.U. Gerber.
of a random variable
with an ExtNegBin(m, r, p) distribution is given by
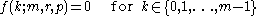
and
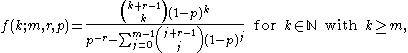
where
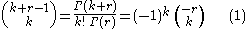
is the (generalized) binomial coefficient
and Γ denotes the gamma function
.
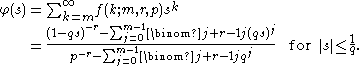
For the important case m = 1, hence r in (–1,0), this simplifies to

Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
and statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
the extended negative binomial distribution is a discrete probability distribution extending the negative binomial distribution
Negative binomial distribution
In probability theory and statistics, the negative binomial distribution is a discrete probability distribution of the number of successes in a sequence of Bernoulli trials before a specified number of failures occur...
. It is a truncated
Truncated distribution
In statistics, a truncated distribution is a conditional distribution that results from restricting the domain of some other probability distribution. Truncated distributions arise in practical statistics in cases where the ability to record, or even to know about, occurrences is limited to values...
version of the negative binomial distribution for which estimation methods have been studied.
In the context of actuarial science
Actuarial science
Actuarial science is the discipline that applies mathematical and statistical methods to assess risk in the insurance and finance industries. Actuaries are professionals who are qualified in this field through education and experience...
, the distribution appeared in its general form in a paper by K. Hess, A. Liewald and K.D. Schmidt when they characterized all distributions for which the extended Panjer recursion
Panjer recursion
The Panjer recursion is an algorithm to compute the probability distribution of a compound random variablewhere both N\, and X_i\, are random variables and of special types. In more general cases the distribution of S is a compound distribution. The recursion for the special cases considered was...
works. For the case m = 1, the distribution was already discussed by Willmot and put into a parametrized family with the logarithmic distribution and the negative binomial distribution by H.U. Gerber.
Probability mass function
For a natural number m ≥ 1 and real parameters p, r with 0 ≤ p < 1 and –m < r < –m + 1, the probability mass functionProbability mass function
In probability theory and statistics, a probability mass function is a function that gives the probability that a discrete random variable is exactly equal to some value...
of a random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
with an ExtNegBin(m, r, p) distribution is given by
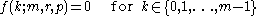
and
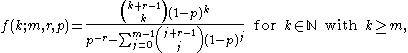
where
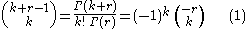
is the (generalized) binomial coefficient
Binomial coefficient
In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
and Γ denotes the gamma function
Gamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
.
Probability generating function
Using the above binomial series representation and the abbreviation q = 1 − p, it follows that the probability generating function is given by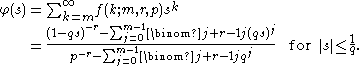
For the important case m = 1, hence r in (–1,0), this simplifies to


