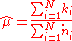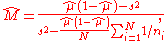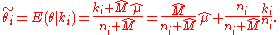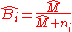Beta-binomial model
Encyclopedia
In probability theory
and statistics
, the beta-binomial distribution is a family of discrete probability distribution
s on a finite support arising when the probability of success in each of a fixed or known number of Bernoulli trials is either unknown or random. It is frequently used in Bayesian statistics
, empirical Bayes methods and classical statistics as an overdispersed
binomial distribution.
It reduces to the Bernoulli distribution as a special case when n = 1. For α = β = 1, it is the discrete uniform distribution from 0 to n. It also approximates the binomial distribution arbitrarily well for large α and β. The beta-binomial is a one-dimensional version of the multivariate Pólya distribution
, as the binomial and beta distributions are special cases of the multinomial and Dirichlet distributions, respectively.
of the binomial distribution. This fact leads to an analytically tractable compound distribution where one can think of the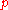 parameter in the binomial distribution as being randomly drawn from a beta distribution. Namely, if
parameter in the binomial distribution as being randomly drawn from a beta distribution. Namely, if
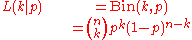
is the binomial distribution where p is a random variable
with a beta distribution
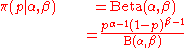
then the compound distribution is given by
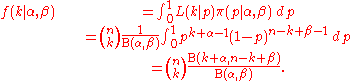
Using the properties of the beta function, this can alternatively be written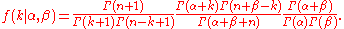
It is within this context that the beta-binomial distribution appears often in Bayesian statistics: the beta-binomial is the predictive distribution of a binomial random variable with a beta distribution prior
on the success probability.
values of α and β. Specifically, imagine an urn containing α red balls and β black balls, where random draws are made. If a red ball is observed, then two red balls are returned to the urn. Likewise, if a black ball is drawn, it is replaced and another black ball is added to the urn. If this is repeated n times, then the probability of observing k red balls follows a beta-binomial distribution with parameters n,α and β.
Note that if the random draws are with simple replacement (no balls over and above the observed ball are added to the urn), then the distribution follows a binomial distribution and if the random draws are made without replacement, the distribution follows a hypergeometric distribution.
are
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
and statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the beta-binomial distribution is a family of discrete probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
s on a finite support arising when the probability of success in each of a fixed or known number of Bernoulli trials is either unknown or random. It is frequently used in Bayesian statistics
Bayesian statistics
Bayesian statistics is that subset of the entire field of statistics in which the evidence about the true state of the world is expressed in terms of degrees of belief or, more specifically, Bayesian probabilities...
, empirical Bayes methods and classical statistics as an overdispersed
Overdispersion
In statistics, overdispersion is the presence of greater variability in a data set than would be expected based on a given simple statistical model....
binomial distribution.
It reduces to the Bernoulli distribution as a special case when n = 1. For α = β = 1, it is the discrete uniform distribution from 0 to n. It also approximates the binomial distribution arbitrarily well for large α and β. The beta-binomial is a one-dimensional version of the multivariate Pólya distribution
Multivariate Polya distribution
The multivariate Pólya distribution, named after George Pólya, also called the Dirichlet compound multinomial distribution, is a compound probability distribution, where a probability vector p is drawn from a Dirichlet distribution with parameter vector \alpha, and a set of discrete samples is...
, as the binomial and beta distributions are special cases of the multinomial and Dirichlet distributions, respectively.
Beta-binomial distribution as a compound distribution
The Beta distribution is a conjugate distributionConjugate prior
In Bayesian probability theory, if the posterior distributions p are in the same family as the prior probability distribution p, the prior and posterior are then called conjugate distributions, and the prior is called a conjugate prior for the likelihood...
of the binomial distribution. This fact leads to an analytically tractable compound distribution where one can think of the
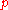 parameter in the binomial distribution as being randomly drawn from a beta distribution. Namely, if
parameter in the binomial distribution as being randomly drawn from a beta distribution. Namely, if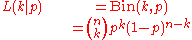
is the binomial distribution where p is a random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
with a beta distribution
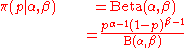
then the compound distribution is given by
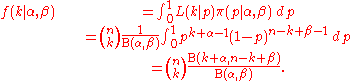
Using the properties of the beta function, this can alternatively be written
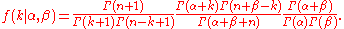
It is within this context that the beta-binomial distribution appears often in Bayesian statistics: the beta-binomial is the predictive distribution of a binomial random variable with a beta distribution prior
Prior probability
In Bayesian statistical inference, a prior probability distribution, often called simply the prior, of an uncertain quantity p is the probability distribution that would express one's uncertainty about p before the "data"...
on the success probability.
Beta-binomial as an urn model
The beta-binomial distribution can also be motivated via an urn model for positive integerInteger
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
values of α and β. Specifically, imagine an urn containing α red balls and β black balls, where random draws are made. If a red ball is observed, then two red balls are returned to the urn. Likewise, if a black ball is drawn, it is replaced and another black ball is added to the urn. If this is repeated n times, then the probability of observing k red balls follows a beta-binomial distribution with parameters n,α and β.
Note that if the random draws are with simple replacement (no balls over and above the observed ball are added to the urn), then the distribution follows a binomial distribution and if the random draws are made without replacement, the distribution follows a hypergeometric distribution.
Moments and properties
The first three raw momentsMoment (mathematics)
In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...
are
-

and the kurtosisKurtosisIn probability theory and statistics, kurtosis is any measure of the "peakedness" of the probability distribution of a real-valued random variable...
is-
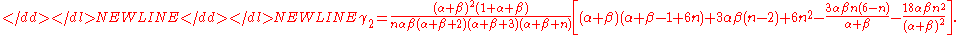
Letting we note, suggestively, that the mean can be written as
we note, suggestively, that the mean can be written as
-
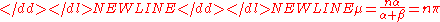
and the variance as
-
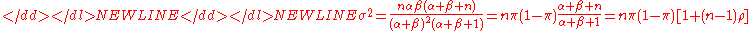
where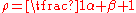 is the correlation between the n Bernoulli draws and is called the over-dispersion parameter.
is the correlation between the n Bernoulli draws and is called the over-dispersion parameter.
Method of moments
The method of moments estimates can be gained by noting the first and second moments of the beta-binomial namely
-

and setting these raw moments equal to the sample moments
-
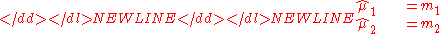
and solving for α and β we get
-

Note that these estimates can be non-sensically negative which is evidence that the data is either undispersed or underdispersed relative to the binomial distribution. In this case, the binomial distribution and the hypergeometric distribution are alternative candidates respectively.
Maximum likelihood estimation
While closed-form maximum likelihood estimatesMaximum likelihoodIn statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....
are impractical, given that the pdf consists of common functions (gamma function and/or Beta functions), they can be easily found via direct numerical optimization. Maximum likelihood estimates from empirical data can be computed using general methods for fitting multinomial Pólya distributions, methods for which are described in (Minka 2003).
The RR (programming language)R is a programming language and software environment for statistical computing and graphics. The R language is widely used among statisticians for developing statistical software, and R is widely used for statistical software development and data analysis....
package VGAM through the function vglm, via maximum likelihood, facilitates the fitting of glmGeneralized linear modelIn statistics, the generalized linear model is a flexible generalization of ordinary linear regression. The GLM generalizes linear regression by allowing the linear model to be related to the response variable via a link function and by allowing the magnitude of the variance of each measurement to...
type models with responses distributed according to the beta-binomial distribution. Note also that there is no requirement that n is fixed throughout the observations.
Example
The following data gives the number of male children among the first 12 children of family size 13 in 6115 families taken from hospital records in 19th century SaxonySaxonyThe Free State of Saxony is a landlocked state of Germany, contingent with Brandenburg, Saxony Anhalt, Thuringia, Bavaria, the Czech Republic and Poland. It is the tenth-largest German state in area, with of Germany's sixteen states....
(Sokal and Rohlf, p. 59 from Lindsey). The 13th child is ignored to assuage the effect of families non-randomly stopping when a desired gender is reached.Males 0 1 2 3 4 5 6 7 8 9 10 11 12 Families 3 24 104 286 670 1033 1343 1112 829 478 181 45 7
We note the first two sample moments are-
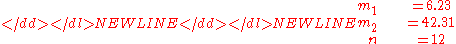
and therefore the method of moments estimates are
-
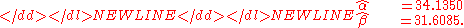
The maximum likelihoodMaximum likelihoodIn statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....
estimates can be found numerically-
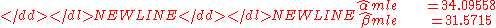
and the maximized log-liklihood is
-

from which we find the AICAkaike information criterionThe Akaike information criterion is a measure of the relative goodness of fit of a statistical model. It was developed by Hirotsugu Akaike, under the name of "an information criterion" , and was first published by Akaike in 1974...
-

The AIC for the competing binomial model is AIC = 25070.34 and thus we see that the beta-binomial model provides a superior fit to the data i.e. there is evidence for overdispersion. Trivers and Willard posit a theoretical justification for heterogeneity in gender-proneness among families (i.e. overdispersion).
The superior fit is evident especially among the tails
Males 0 1 2 3 4 5 6 7 8 9 10 11 12 Observed Families 3 24 104 286 670 1033 1343 1112 829 478 181 45 7 Predicted (Beta-Binomial) 2.3 22.6 104.8 310.9 655.7 1036.2 1257.9 1182.1 853.6 461.9 177.9 43.8 5.2 Predicted (Binomial p = 0.519215) 0.9 12.1 71.8 258.5 628.1 1085.2 1367.3 1265.6 854.2 410.0 132.8 26.1 2.3
Further Bayesian considerations
It is convenient to reparameterize the distributions so that the expected mean of the prior is a single parameter: Let
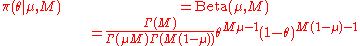
where
-
-
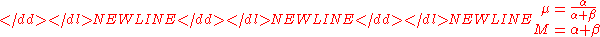
so that
-
-

The posterior distribution ρ(θ|k) is also a beta distribution:

And
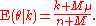
while the marginal distribution m(k|μ, M) is given by
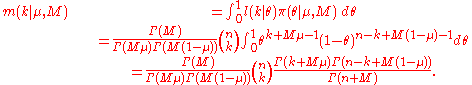
Because the marginal is a complex, non-linear function of Gamma and Digamma functions, it is quite difficult to obtain a marginal maximum likelihood estimate (MMLE) for the mean and variance. Instead, we use the method of iterated expectations to find the expected valueExpected valueIn probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
of the marginal moments.
Let us write our model as a two-stage compound sampling model. Let ki be the number of success out of ni trials for event i:
-

We can find iterated moment estimates for the mean and variance using the moments for the distributions in the two-stage model:
-
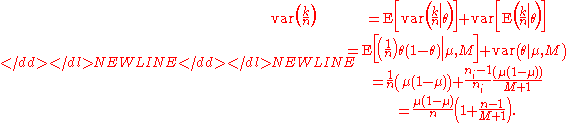
(Here we have used the law of total expectationLaw of total expectationThe proposition in probability theory known as the law of total expectation, the law of iterated expectations, the tower rule, the smoothing theorem, among other names, states that if X is an integrable random variable The proposition in probability theory known as the law of total expectation, ...
and the law of total varianceLaw of total varianceIn probability theory, the law of total variance or variance decomposition formula states that if X and Y are random variables on the same probability space, and the variance of Y is finite, then...
.)
We want point estimates for and
and  . The estimated mean
. The estimated mean 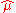 is calculated from the sample
is calculated from the sample
The estimate of the hyperparameter M is obtained using the moment estimates for the variance of the two-stage model:
-

Solving:
where
-

Since we now have parameter point estimates, and
and  , for the underlying distribution, we would like to find a point estimate
, for the underlying distribution, we would like to find a point estimate 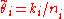 for the probability of success for event i. This is the weighted average of the event estimate
for the probability of success for event i. This is the weighted average of the event estimate  and
and 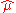 . Given our point estimates for the prior, we may now plug in these values to find a point estimate for the posterior
. Given our point estimates for the prior, we may now plug in these values to find a point estimate for the posterior
Shrinkage factors
We may write the posterior estimate as a weighted average:
where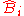 is called the shrinkage factor.
is called the shrinkage factor.
Related distributions
 where
where 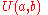 is the discrete uniform distribution.
is the discrete uniform distribution.
External links
- Using the Beta-binomial distribution to assess performance of a biometric identification device
- Fastfit contains Matlab code for fitting Beta-Binomial distributions (in the form of two-dimensional Pólya distributions) to data.
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-