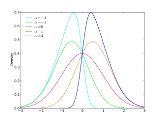
Skew normal distribution
Encyclopedia
In probability theory
and statistics
, the skew normal distribution is a continuous probability distribution that generalises the normal distribution to allow for non-zero skewness
.
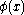denote the standard normal probability density function
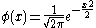
with the cumulative distribution function
given by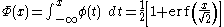
where erf is the error function
. Then the probability density function of the skew-normal distribution with parameter α is given by
This distribution was first introduced by O'Hagan and Leonhard (1976).
To add location
and scale
parameters to this, one makes the usual transform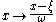
. One can verify that the normal distribution is recovered when 
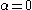, and that the absolute value of the skewness increases as the absolute value of 
increases. The distribution is right skewed if 
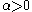and is left skewed if 
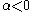. The probability density function with location 
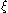, scale 
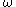, and parameter 
becomes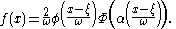
estimates for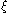
, 
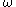, and 
can be computed numerically, but no closed-form expression for the estimates is available unless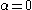 
. If a closed-form expression is needed, the method of moments can be applied to estimate 
from the sample skew, by inverting the skewness equation. This yields the estimate
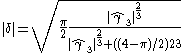
where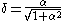
, and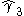 
is the sample skew. The sign of 
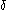is the same as the sign of 
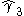. Consequently, 
.
The maximum (theoretical) skewness is obtained by setting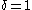
in the skewness equation, giving 
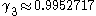. However it is possible that the sample skewness is larger, and then 
cannot be determined from these equations. When using the method of moments in an automatic fashion, for example to give starting values for maximum likelihood iteration, one should therefore let (for example)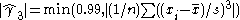 
.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
and statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the skew normal distribution is a continuous probability distribution that generalises the normal distribution to allow for non-zero skewness
Skewness
In probability theory and statistics, skewness is a measure of the asymmetry of the probability distribution of a real-valued random variable. The skewness value can be positive or negative, or even undefined...
.
Definition
Let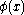 denote the standard normal probability density functionProbability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
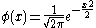
with the cumulative distribution function
Cumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
given by
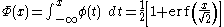
where erf is the error function
Error function
In mathematics, the error function is a special function of sigmoid shape which occurs in probability, statistics and partial differential equations...
. Then the probability density function of the skew-normal distribution with parameter α is given by
This distribution was first introduced by O'Hagan and Leonhard (1976).
To add location
Location parameter
In statistics, a location family is a class of probability distributions that is parametrized by a scalar- or vector-valued parameter μ, which determines the "location" or shift of the distribution...
and scale
Scale parameter
In probability theory and statistics, a scale parameter is a special kind of numerical parameter of a parametric family of probability distributions...
parameters to this, one makes the usual transform
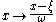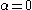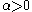. One can verify that the normal distribution is recovered when , and that the absolute value of the skewness increases as the absolute value of increases. The distribution is right skewed if and is left skewed if 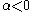. The probability density function with location 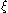, scale 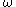, and parameter becomes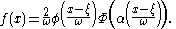Estimation
Maximum likelihoodMaximum likelihood
In statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....
estimates for
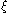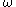, , and can be computed numerically, but no closed-form expression for the estimates is available unless 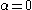. If a closed-form expression is needed, the method of moments can be applied to estimate from the sample skew, by inverting the skewness equation. This yields the estimate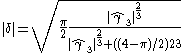where
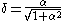, and 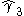is the sample skew. The sign of 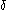is the same as the sign of 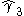. Consequently, .The maximum (theoretical) skewness is obtained by setting
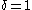in the skewness equation, giving 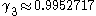. However it is possible that the sample skewness is larger, and then cannot be determined from these equations. When using the method of moments in an automatic fashion, for example to give starting values for maximum likelihood iteration, one should therefore let (for example) 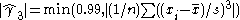.See also
- Normal distribution
- Generalized normal distribution
- Lognormal distribution
- SkewnessSkewnessIn probability theory and statistics, skewness is a measure of the asymmetry of the probability distribution of a real-valued random variable. The skewness value can be positive or negative, or even undefined...