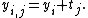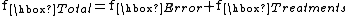Analysis of variance
Encyclopedia
In statistics
, analysis of variance (ANOVA) is a collection of statistical model
s, and their associated procedures, in which the observed variance
in a particular variable is partitioned into components attributable to different sources of variation. In its simplest form ANOVA provides a statistical test of whether or not the mean
s of several groups are all equal, and therefore generalizes t-test to more than two groups. Doing multiple two-sample t-tests would result in an increased chance of committing a type I error. For this reason, ANOVAs are useful in comparing two, three or more means.
that relates the response to the treatments and blocks. Even when the statistical model
is nonlinear
, it can be approximated by a linear model for which an analysis of variance may be appropriate.
, which makes the following assumptions about the probability distribution
of the responses:
To test the hypothesis that all treatments have exactly the same effect, the F-test
's p-values closely approximate the permutation test's p-values: The approximation is particularly close when the design is balanced. Such permutation tests characterize tests with maximum power
against all alternative hypotheses, as observed by Rosenbaum.Rosenbaum (2002, page 40) cites Section 5.7, Theorem 2.3 of Lehmann
's Testing Statistical Hypotheses (1959). The anova F–test (of the null-hypothesis that all treatments have exactly the same effect) is recommended as a practical test, because of its robustness against many alternative distributions.Non-statisticians may be confused because another F-test is nonrobust: When used to test the equality of the variances of two populations, the F-test
is unreliable if there are deviations from normality (Lindman, 1974 ). The Kruskal–Wallis test is a nonparametric alternative that does not rely on an assumption of normality. And the Friedman test
is the nonparametric alternative for a one-way repeated measures ANOVA.
The separate assumptions of the textbook model imply that the errors
are independently, identically, and normally distributed for fixed effects models, that is, that the errors (
's) are independent and
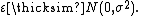
, the treatments are randomly assigned to experimental units, following the experimental protocol. This randomization is objective and declared before the experiment is carried out. The objective random-assignment is used to test the significance of the null hypothesis, following the ideas of C. S. Peirce and Ronald A. Fisher. This design-based analysis was discussed and developed by Francis J. Anscombe at Rothamsted Experimental Station
and by Oscar Kempthorne
at Iowa State University
. Kempthorne and his students make an assumption of unit treatment additivity, which is discussed in the books of Kempthorne and David R. Cox.
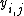from experimental unit 
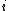when receiving treatment 
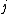can be written as the sum of the unit's response 
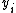and the treatment-effect 
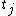, that is
The assumption of unit-treatment addivity implies that, for every treatment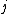
, the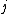 
th treatment have exactly the same effect 
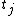on every experiment unit.
The assumption of unit treatment additivity usually cannot be directly falsified, according to Cox and Kempthorne. However, many consequences of treatment-unit additivity can be falsified. For a randomized experiment, the assumption of unit-treatment additivity implies that the variance is constant for all treatments. Therefore, by contraposition
, a necessary condition for unit-treatment additivity is that the variance is constant.
The property of unit-treatment additivity is not invariant under a "change of scale", so statisticians often use transformations to achieve unit-treatment additivity. If the response variable is expected to follow a parametric family of probability distributions, then the statistician may specify (in the protocol for the experiment or observational study) that the responses be transformed to stabilize the variance. Also, a statistician may specify that logarithmic transforms be applied to the responses, which are believed to follow a multiplicative model.
According to Cauchy's functional equation
theorem, the logarithm
is the only continuous transformation that transforms real multiplication to addition.
The assumption of unit-treatment additivity was enunciated in experimental design by Kempthorne and Cox. Kempthorne's use of unit treatment additivity and randomization is similar to the design-based inference that is standard in finite-population survey sampling
.
The test statistics of this derived linear model are closely approximated by the test statistics of an appropriate normal linear model, according to approximation theorems and simulation studies by Kempthorne and his students (Hinkelmann and Kempthorne 2008). However, there are differences. For example, the randomization-based analysis results in a small but (strictly) negative correlation between the observations. In the randomization-based analysis, there is no assumption of a normal distribution and certainly no assumption of independence. On the contrary, the observations are dependent!
The randomization-based analysis has the disadvantage that its exposition involves tedious algebra and extensive time. Since the randomization-based analysis is complicated and is closely approximated by the approach using a normal linear model, most teachers emphasize the normal linear model approach. Few statisticians object to model-based analysis of balanced randomized experiments.
So, the number of degrees of freedom
f can be partitioned in a similar way and specifies the chi-squared distribution which describes the associated sums of squares.
See also Lack-of-fit sum of squares
.
is used for comparisons of the components of the total deviation. For example, in one-way, or single-factor ANOVA, statistical significance is tested for by comparing the F test statistic
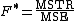
where
I = number of treatments
and
nT = total number of cases
to the F-distribution with I − 1,nT − I degrees of freedom. Using the F-distribution is a natural candidate because the test statistic is the ratio of two scaled sums of squares each of which follows a scaled chi-squared distribution.
is often applied in the context of ANOVA in order to assess the probability of successfully rejecting the null hypothesis if we assume a certain ANOVA design, effect size in the population, sample size and alpha level. Power analysis can assist in study design by determining what sample size would be required in order to have a reasonable chance of rejecting the null hypothesis when the alternative hypothesis is true.
include the following: eta-squared, partial eta-squared, omega, and intercorrelation.
η2 ( eta-squared ):
Eta-squared describes the ratio of variance explained in the dependent variable by a predictor while controlling for other predictors. Eta-squared is a biased estimator of the variance explained by the model in the population (it estimates only the effect size in the sample). On average it overestimates the variance explained in the population. As the sample size gets larger the amount of bias gets smaller,
Partial η2 (Partial eta-squared):
Partial eta-squared describes the "proportion of total variation attributable to the factor, partialling out (excluding) other factors from the total nonerror variation". Partial eta squared is often higher than eta squared,
Cohen (1992) suggests effect sizes for various indexes, including ƒ (where 0.1 is a small effect, 0.25 is a medium effect and 0.4 is a large effect). He also offers a conversion table (see Cohen, 1988, p. 283) for eta squared (η2) where 0.0099 constitutes a small effect, 0.0588 a medium effect and 0.1379 a large effect. Though, considering that η2 are comparable to r2 when df of the numerator equals 1 (both measures' proportion of variance accounted for), these guidelines may overestimate the size of the effect. If going by the r guidelines (0.1 is a small effect, 0.3 a medium effect and 0.5 a large effect) then the equivalent guidelines for eta-squared would be the square of these, i.e. 0.01 is a small effect, 0.09 a medium effect and 0.25 a large effect, and these should also be applicable to eta-squared. When the df of the numerator exceeds 1, eta-squared is comparable to R-squared.
Omega2 ( omega-squared ):
A more unbiased estimator of the variance explained in the population is omega-squared
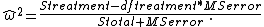
While this form of the formula is limited to between-subjects analysis with equal sample sizes in all cells, a generalized form of the estimator has been published for between-subjects and within-subjects analysis, repeated measure, mixed design, and randomized block design experiments. In addition, methods to calculate partial Omega2 for individual factors and combined factors in designs with up to three independent variables have been published.
Cohen's ƒ2: This measure of effect size represents the square root of variance explained over variance not explained.
SMCV or standardized mean of a contrast variable
:
This effect size
is the ratio of mean
to standard deviation
of a contrast variable for contrast analysis in ANOVA. It may provide a probabilistic interpretation to various effect sizes in contrast analysis.
Follow-up tests are often distinguished in terms of whether they are planned (a priori) or post hoc
. Planned tests are determined before looking at the data and post hoc tests are performed after looking at the data.
Post hoc tests such as Tukey's range test most commonly compare every group mean with every other group mean and typically incorporate some method of controlling for Type I errors.
Comparisons, which are most commonly planned, can be either simple or compound. Simple comparisons compare one group mean with one other group mean. Compound comparisons typically compare two sets of groups means where one set has two or more groups (e.g., compare average group means of group A, B and C with group D). Comparisons can also look at tests of trend, such as linear and quadratic relationships, when the independent variable involves ordered levels.
of treatments to subjects; the protocol's description of the assignment mechanism should include a specification of the structure of the treatments and of any blocking
. It is also common to apply ANOVA to observational data using an appropriate statistical model.
Some popular designs use the following types of ANOVA:
Sir Ronald Fisher proposed a formal analysis of variance
in a 1918 article The Correlation Between Relatives on the Supposition of Mendelian Inheritance
. His first application of the analysis of variance was published in 1921. Analysis of variance became widely known after being included in Fisher's 1925 book Statistical Methods for Research Workers
.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, analysis of variance (ANOVA) is a collection of statistical model
Statistical model
A statistical model is a formalization of relationships between variables in the form of mathematical equations. A statistical model describes how one or more random variables are related to one or more random variables. The model is statistical as the variables are not deterministically but...
s, and their associated procedures, in which the observed variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
in a particular variable is partitioned into components attributable to different sources of variation. In its simplest form ANOVA provides a statistical test of whether or not the mean
Mean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
s of several groups are all equal, and therefore generalizes t-test to more than two groups. Doing multiple two-sample t-tests would result in an increased chance of committing a type I error. For this reason, ANOVAs are useful in comparing two, three or more means.
Models
There are three classes of models used in the analysis of variance, and these are outlined here.Fixed-effects models (Model 1)
The fixed-effects model of analysis of variance applies to situations in which the experimenter applies one or more treatments to the subjects of the experiment to see if the response variable values change. This allows the experimenter to estimate the ranges of response variable values that the treatment would generate in the population as a whole.Random-effects models (Model 2)
Random effects models are used when the treatments are not fixed. This occurs when the various factor levels are sampled from a larger population. Because the levels themselves are random variables, some assumptions and the method of contrasting the treatments differ from ANOVA model 1.Mixed-effects models (Model 3)
A mixed-effects model contains experimental factors of both fixed and random-effects types, with appropriately different interpretations and analysis for the two types.Assumptions of ANOVA
The analysis of variance has been studied from several approaches, the most common of which use a linear modelLinear model
In statistics, the term linear model is used in different ways according to the context. The most common occurrence is in connection with regression models and the term is often taken as synonymous with linear regression model. However the term is also used in time series analysis with a different...
that relates the response to the treatments and blocks. Even when the statistical model
Statistical model
A statistical model is a formalization of relationships between variables in the form of mathematical equations. A statistical model describes how one or more random variables are related to one or more random variables. The model is statistical as the variables are not deterministically but...
is nonlinear
Nonlinear regression
In statistics, nonlinear regression is a form of regression analysis in which observational data are modeled by a function which is a nonlinear combination of the model parameters and depends on one or more independent variables...
, it can be approximated by a linear model for which an analysis of variance may be appropriate.
A model often presented in textbooks
Many textbooks present the analysis of variance in terms of a linear modelLinear model
In statistics, the term linear model is used in different ways according to the context. The most common occurrence is in connection with regression models and the term is often taken as synonymous with linear regression model. However the term is also used in time series analysis with a different...
, which makes the following assumptions about the probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
of the responses:
- IndependenceStatistical independenceIn probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
of cases – this is an assumption of the model that simplifies the statistical analysis. - Normality – the distributions of the residuals are normal.
- Equality (or "homogeneity") of variances, called homoscedasticityHomoscedasticityIn statistics, a sequence or a vector of random variables is homoscedastic if all random variables in the sequence or vector have the same finite variance. This is also known as homogeneity of variance. The complementary notion is called heteroscedasticity...
— the variance of data in groups should be the same. Model-based approaches usually assume that the variance is constant. The constant-variance property also appears in the randomization (design-based) analysis of randomized experiments, where it is a necessary consequence of the randomized design and the assumption of unit treatment additivity. If the responses of a randomized balanced experiment fail to have constant variance, then the assumption of unit treatment additivity is necessarily violated.
To test the hypothesis that all treatments have exactly the same effect, the F-test
F-test
An F-test is any statistical test in which the test statistic has an F-distribution under the null hypothesis.It is most often used when comparing statistical models that have been fit to a data set, in order to identify the model that best fits the population from which the data were sampled. ...
's p-values closely approximate the permutation test's p-values: The approximation is particularly close when the design is balanced. Such permutation tests characterize tests with maximum power
Uniformly most powerful test
In statistical hypothesis testing, a uniformly most powerful test is a hypothesis test which has the greatest power 1 − β among all possible tests of a given size α...
against all alternative hypotheses, as observed by Rosenbaum.Rosenbaum (2002, page 40) cites Section 5.7, Theorem 2.3 of Lehmann
Erich Leo Lehmann
Erich Leo Lehmann was an American statistician, who contributed to statistical and nonparametric hypothesis testing...
's Testing Statistical Hypotheses (1959). The anova F–test (of the null-hypothesis that all treatments have exactly the same effect) is recommended as a practical test, because of its robustness against many alternative distributions.Non-statisticians may be confused because another F-test is nonrobust: When used to test the equality of the variances of two populations, the F-test
F-test
An F-test is any statistical test in which the test statistic has an F-distribution under the null hypothesis.It is most often used when comparing statistical models that have been fit to a data set, in order to identify the model that best fits the population from which the data were sampled. ...
is unreliable if there are deviations from normality (Lindman, 1974 ). The Kruskal–Wallis test is a nonparametric alternative that does not rely on an assumption of normality. And the Friedman test
Friedman test
The Friedman test is a non-parametric statistical test developed by the U.S. economist Milton Friedman. Similar to the parametric repeated measures ANOVA, it is used to detect differences in treatments across multiple test attempts. The procedure involves ranking each row together, then...
is the nonparametric alternative for a one-way repeated measures ANOVA.
The separate assumptions of the textbook model imply that the errors
Errors and residuals in statistics
In statistics and optimization, statistical errors and residuals are two closely related and easily confused measures of the deviation of a sample from its "theoretical value"...
are independently, identically, and normally distributed for fixed effects models, that is, that the errors (
's) are independent and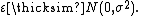Randomization-based analysis
In a randomized controlled experimentRandomized controlled trial
A randomized controlled trial is a type of scientific experiment - a form of clinical trial - most commonly used in testing the safety and efficacy or effectiveness of healthcare services or health technologies A randomized controlled trial (RCT) is a type of scientific experiment - a form of...
, the treatments are randomly assigned to experimental units, following the experimental protocol. This randomization is objective and declared before the experiment is carried out. The objective random-assignment is used to test the significance of the null hypothesis, following the ideas of C. S. Peirce and Ronald A. Fisher. This design-based analysis was discussed and developed by Francis J. Anscombe at Rothamsted Experimental Station
Rothamsted Experimental Station
The Rothamsted Experimental Station, one of the oldest agricultural research institutions in the world, is located at Harpenden in Hertfordshire, England. It is now known as Rothamsted Research...
and by Oscar Kempthorne
Oscar Kempthorne
Oscar Kempthorne was a statistician and geneticist known for his research on randomization-analysis and the design of experiments, which had wide influence on research in agriculture, genetics, and other areas of science...
at Iowa State University
Iowa State University
Iowa State University of Science and Technology, more commonly known as Iowa State University , is a public land-grant and space-grant research university located in Ames, Iowa, United States. Iowa State has produced astronauts, scientists, and Nobel and Pulitzer Prize winners, along with a host of...
. Kempthorne and his students make an assumption of unit treatment additivity, which is discussed in the books of Kempthorne and David R. Cox.
Unit-treatment additivity
In its simplest form, the assumption of unit-treatment additivity states that the observed response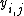 from experimental unit 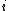when receiving treatment 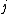can be written as the sum of the unit's response 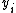and the treatment-effect 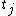, that is
The assumption of unit-treatment addivity implies that, for every treatment
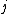, the 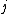th treatment have exactly the same effect 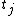on every experiment unit.The assumption of unit treatment additivity usually cannot be directly falsified, according to Cox and Kempthorne. However, many consequences of treatment-unit additivity can be falsified. For a randomized experiment, the assumption of unit-treatment additivity implies that the variance is constant for all treatments. Therefore, by contraposition
Contraposition
In traditional logic, contraposition is a form of immediate inference in which from a given proposition another is inferred having for its subject the contradictory of the original predicate, and in some cases involving a change of quality . For its symbolic expression in modern logic see the rule...
, a necessary condition for unit-treatment additivity is that the variance is constant.
The property of unit-treatment additivity is not invariant under a "change of scale", so statisticians often use transformations to achieve unit-treatment additivity. If the response variable is expected to follow a parametric family of probability distributions, then the statistician may specify (in the protocol for the experiment or observational study) that the responses be transformed to stabilize the variance. Also, a statistician may specify that logarithmic transforms be applied to the responses, which are believed to follow a multiplicative model.
According to Cauchy's functional equation
Functional equation
In mathematics, a functional equation is any equation that specifies a function in implicit form.Often, the equation relates the value of a function at some point with its values at other points. For instance, properties of functions can be determined by considering the types of functional...
theorem, the logarithm
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
is the only continuous transformation that transforms real multiplication to addition.
The assumption of unit-treatment additivity was enunciated in experimental design by Kempthorne and Cox. Kempthorne's use of unit treatment additivity and randomization is similar to the design-based inference that is standard in finite-population survey sampling
Survey sampling
In statistics, survey sampling describes the process of selecting a sample of elements from a target population in order to conduct a survey.A survey may refer to many different types or techniques of observation, but in the context of survey sampling it most often involves a questionnaire used to...
.
Derived linear model
Kempthorne uses the randomization-distribution and the assumption of unit treatment additivity to produce a derived linear model, very similar to the textbook model discussed previously.The test statistics of this derived linear model are closely approximated by the test statistics of an appropriate normal linear model, according to approximation theorems and simulation studies by Kempthorne and his students (Hinkelmann and Kempthorne 2008). However, there are differences. For example, the randomization-based analysis results in a small but (strictly) negative correlation between the observations. In the randomization-based analysis, there is no assumption of a normal distribution and certainly no assumption of independence. On the contrary, the observations are dependent!
The randomization-based analysis has the disadvantage that its exposition involves tedious algebra and extensive time. Since the randomization-based analysis is complicated and is closely approximated by the approach using a normal linear model, most teachers emphasize the normal linear model approach. Few statisticians object to model-based analysis of balanced randomized experiments.
Statistical models for observational data
However, when applied to data from non-randomized experiments or observational studies, model-based analysis lacks the warrant of randomization. For observational data, the derivation of confidence intervals must use subjective models, as emphasized by Ronald A. Fisher and his followers. In practice, the estimates of treatment-effects from observational studies generally are often inconsistent. In practice, "statistical models" and observational data are useful for suggesting hypotheses that should be treated very cautiously by the public.Partitioning of the sum of squares
The fundamental technique is a partitioning of the total sum of squares S into components related to the effects used in the model. For example, we show the model for a simplified ANOVA with one type of treatment at different levels.
So, the number of degrees of freedom
Degrees of freedom (statistics)
In statistics, the number of degrees of freedom is the number of values in the final calculation of a statistic that are free to vary.Estimates of statistical parameters can be based upon different amounts of information or data. The number of independent pieces of information that go into the...
f can be partitioned in a similar way and specifies the chi-squared distribution which describes the associated sums of squares.
See also Lack-of-fit sum of squares
Lack-of-fit sum of squares
In statistics, a sum of squares due to lack of fit, or more tersely a lack-of-fit sum of squares, is one of the components of a partition of the sum of squares in an analysis of variance, used in the numerator in an F-test of the null hypothesis that says that a proposed model fits well.- Sketch of...
.
The F-test
The F-testF-test
An F-test is any statistical test in which the test statistic has an F-distribution under the null hypothesis.It is most often used when comparing statistical models that have been fit to a data set, in order to identify the model that best fits the population from which the data were sampled. ...
is used for comparisons of the components of the total deviation. For example, in one-way, or single-factor ANOVA, statistical significance is tested for by comparing the F test statistic
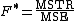
where
I = number of treatmentsand
nT = total number of casesto the F-distribution with I − 1,nT − I degrees of freedom. Using the F-distribution is a natural candidate because the test statistic is the ratio of two scaled sums of squares each of which follows a scaled chi-squared distribution.
Power analysis
Power analysisStatistical power
The power of a statistical test is the probability that the test will reject the null hypothesis when the null hypothesis is actually false . The power is in general a function of the possible distributions, often determined by a parameter, under the alternative hypothesis...
is often applied in the context of ANOVA in order to assess the probability of successfully rejecting the null hypothesis if we assume a certain ANOVA design, effect size in the population, sample size and alpha level. Power analysis can assist in study design by determining what sample size would be required in order to have a reasonable chance of rejecting the null hypothesis when the alternative hypothesis is true.
Effect size
Several standardized measures of effect gauge the strength of the association between a predictor (or set of predictors) and the dependent variable. Effect-size estimates facilitate the comparison of findings in studies and across disciplines. Common effect size estimates reported in univariate-response anova and multivariate-response manovaMANOVA
Multivariate analysis of variance is a generalized form of univariate analysis of variance . It is used when there are two or more dependent variables. It helps to answer : 1. do changes in the independent variable have significant effects on the dependent variables; 2. what are the interactions...
include the following: eta-squared, partial eta-squared, omega, and intercorrelation.
η2 ( eta-squared ):
Eta-squared describes the ratio of variance explained in the dependent variable by a predictor while controlling for other predictors. Eta-squared is a biased estimator of the variance explained by the model in the population (it estimates only the effect size in the sample). On average it overestimates the variance explained in the population. As the sample size gets larger the amount of bias gets smaller,
Partial η2 (Partial eta-squared):
Partial eta-squared describes the "proportion of total variation attributable to the factor, partialling out (excluding) other factors from the total nonerror variation". Partial eta squared is often higher than eta squared,
Cohen (1992) suggests effect sizes for various indexes, including ƒ (where 0.1 is a small effect, 0.25 is a medium effect and 0.4 is a large effect). He also offers a conversion table (see Cohen, 1988, p. 283) for eta squared (η2) where 0.0099 constitutes a small effect, 0.0588 a medium effect and 0.1379 a large effect. Though, considering that η2 are comparable to r2 when df of the numerator equals 1 (both measures' proportion of variance accounted for), these guidelines may overestimate the size of the effect. If going by the r guidelines (0.1 is a small effect, 0.3 a medium effect and 0.5 a large effect) then the equivalent guidelines for eta-squared would be the square of these, i.e. 0.01 is a small effect, 0.09 a medium effect and 0.25 a large effect, and these should also be applicable to eta-squared. When the df of the numerator exceeds 1, eta-squared is comparable to R-squared.
Omega2 ( omega-squared ):
A more unbiased estimator of the variance explained in the population is omega-squared
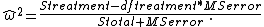
While this form of the formula is limited to between-subjects analysis with equal sample sizes in all cells, a generalized form of the estimator has been published for between-subjects and within-subjects analysis, repeated measure, mixed design, and randomized block design experiments. In addition, methods to calculate partial Omega2 for individual factors and combined factors in designs with up to three independent variables have been published.
Cohen's ƒ2: This measure of effect size represents the square root of variance explained over variance not explained.
SMCV or standardized mean of a contrast variable
Standardized mean of a contrast variable
In statistics, the standardized mean of a contrast variable , is a parameter assessing effect size. The SMCV is defined as mean divided by the standard deviation of a contrast variable.The SMCV was first proposed for one-way ANOVA cases...
:
This effect size
Effect size
In statistics, an effect size is a measure of the strength of the relationship between two variables in a statistical population, or a sample-based estimate of that quantity...
is the ratio of mean
Mean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
to standard deviation
Standard deviation
Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
of a contrast variable for contrast analysis in ANOVA. It may provide a probabilistic interpretation to various effect sizes in contrast analysis.
Follow up tests
A statistically significant effect in ANOVA is often followed up with one or more different follow-up tests. This can be done in order to assess which groups are different from which other groups or to test various other focused hypotheses.Follow-up tests are often distinguished in terms of whether they are planned (a priori) or post hoc
Post-hoc analysis
Post-hoc analysis , in the context of design and analysis of experiments, refers to looking at the data—after the experiment has concluded—for patterns that were not specified a priori. It is sometimes called by critics data dredging to evoke the sense that the more one looks the more likely...
. Planned tests are determined before looking at the data and post hoc tests are performed after looking at the data.
Post hoc tests such as Tukey's range test most commonly compare every group mean with every other group mean and typically incorporate some method of controlling for Type I errors.
Comparisons, which are most commonly planned, can be either simple or compound. Simple comparisons compare one group mean with one other group mean. Compound comparisons typically compare two sets of groups means where one set has two or more groups (e.g., compare average group means of group A, B and C with group D). Comparisons can also look at tests of trend, such as linear and quadratic relationships, when the independent variable involves ordered levels.
Study designs and ANOVAs
There are several types of ANOVA. Many statisticians base ANOVA on the design of the experiment, especially on the protocol that specifies the random assignmentRandom assignment
Random assignment or random placement is an experimental technique for assigning subjects to different treatments . The thinking behind random assignment is that by randomizing treatment assignment, then the group attributes for the different treatments will be roughly equivalent and therefore any...
of treatments to subjects; the protocol's description of the assignment mechanism should include a specification of the structure of the treatments and of any blocking
Blocking (statistics)
In the statistical theory of the design of experiments, blocking is the arranging of experimental units in groups that are similar to one another. For example, an experiment is designed to test a new drug on patients. There are two levels of the treatment, drug, and placebo, administered to male...
. It is also common to apply ANOVA to observational data using an appropriate statistical model.
Some popular designs use the following types of ANOVA:
- One-way ANOVAOne-way ANOVAIn statistics, one-way analysis of variance is a technique used to compare means of two or more samples . This technique can be used only for numerical data....
is used to test for differences among two or more independentStatistical independenceIn probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
groups (means),e.g. different levels of urea application in a crop. Typically, however, the one-way ANOVA is used to test for differences among at least three groups, since the two-group case can be covered by a t-test. When there are only two means to compare, the t-test and the ANOVA F-testF-testAn F-test is any statistical test in which the test statistic has an F-distribution under the null hypothesis.It is most often used when comparing statistical models that have been fit to a data set, in order to identify the model that best fits the population from which the data were sampled. ...
are equivalent; the relation between ANOVA and t is given by F = t2. - FactorialFactorial experimentIn statistics, a full factorial experiment is an experiment whose design consists of two or more factors, each with discrete possible values or "levels", and whose experimental units take on all possible combinations of these levels across all such factors. A full factorial design may also be...
ANOVA is used when the experimenter wants to study the interaction effects among the treatments. - Repeated measures ANOVA is used when the same subjects are used for each treatment (e.g., in a longitudinal studyLongitudinal studyA longitudinal study is a correlational research study that involves repeated observations of the same variables over long periods of time — often many decades. It is a type of observational study. Longitudinal studies are often used in psychology to study developmental trends across the...
). - Multivariate analysis of variance (MANOVA) is used when there is more than one response variable.
History
The analysis of variance was used informally by researchers in the 1800s using least squares. In physics and psychology, researchers included a term for the operator-effect, the influence of a particular person on measurements, according to Stephen Stigler's histories.Sir Ronald Fisher proposed a formal analysis of variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
in a 1918 article The Correlation Between Relatives on the Supposition of Mendelian Inheritance
The Correlation Between Relatives on the Supposition of Mendelian Inheritance
The Correlation Between Relatives on the Supposition of Mendelian Inheritance is a scientific paper by R.A. Fisher which was published in the Philosophical Transactions of the Royal Society of Edinburgh in 1918,...
. His first application of the analysis of variance was published in 1921. Analysis of variance became widely known after being included in Fisher's 1925 book Statistical Methods for Research Workers
Statistical Methods for Research Workers
Statistical Methods for Research Workers is a classic 1925 book on statistics by the statistician R.A. Fisher. It is considered by some to be one of the 20th century's most influential books on statistical methods. According to ,...
.
External links
- SOCRSOCRThe Statistics Online Computational Resource is a suite of online tools and interactive aids for hands-on learning and teaching concepts in statistical analysis and probability theory developed at the University of California, Los Angeles...
ANOVA Activity and interactive applet. - One-Way and Two-Way ANOVA in QtiPlot
- Examples of all ANOVA and ANCOVA models with up to three treatment factors, including randomized block, split plot, repeated measures, and Latin squares
- NIST/SEMATECH e-Handbook of Statistical Methods, section 7.4.3: "Are the means equal?"