
Phase-type distribution
Encyclopedia
A phase-type distribution is a probability distribution
that results from a system of one or more inter-related Poisson process
es occurring in sequence
, or phases. The sequence in which each of the phases occur may itself be a stochastic process
. The distribution can be represented by a random variable
describing the time until absorption of a Markov process
with one absorbing state. Each of the state
s of the Markov process represents one of the phases.
It has a discrete time
equivalent the discrete phase-type distribution
.
The set of phase-type distributions is dense in the field of all positive-valued distributions, that is, it can be used to approximate any positive valued distribution.
The continuous phase-type distribution is the distribution of time from the above process's starting until absorption in the absorbing state.
This process can be written in the form of a transition rate matrix,
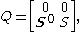
where S is an m×m matrix and S0 = -S1. Here 1 represents an m×1 vector with every element being 1.
The distribution function of X is given by,
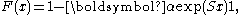
and the density function,
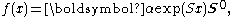
for all x > 0, where exp( · ) is the matrix exponential
. It is usually assumed the probability of process starting in the absorbing state is zero. The moments of the distribution function are given by
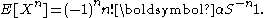
As the phase-type distribution is dense in the field of all positive-valued distributions, we can represent any positive valued distribution. However, the phase-type is a light-tailed or platikurtic distribution. So the representation of heavy-tailed or leptokurtic distribution by phase type is an approximation, even if the precision of the approximation can be as good as we want.
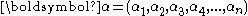
with and
and
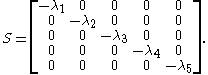
This mixture of densities of exponential distributed random variables can be characterized through
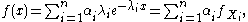
or its cumulative distribution function
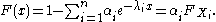
with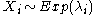
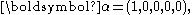
and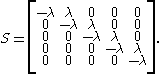
The hypoexponential distribution
is a generalisation of the Erlang distribution by having different rates for each transition (the non-homogeneous case).
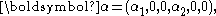
and
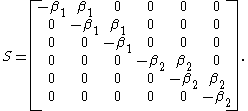

and
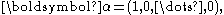
where 0 < p1,...,pk-1 ≤ 1. In the case where all pi = 1 we have the hypoexponential distribution. The Coxian distribution is extremely important as any acyclic phase-type distribution has an equivalent Coxian representation.
The generalised Coxian distribution relaxes the condition that requires starting in the first phase.
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
that results from a system of one or more inter-related Poisson process
Poisson process
A Poisson process, named after the French mathematician Siméon-Denis Poisson , is a stochastic process in which events occur continuously and independently of one another...
es occurring in sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
, or phases. The sequence in which each of the phases occur may itself be a stochastic process
Stochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
. The distribution can be represented by a random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
describing the time until absorption of a Markov process
Markov process
In probability theory and statistics, a Markov process, named after the Russian mathematician Andrey Markov, is a time-varying random phenomenon for which a specific property holds...
with one absorbing state. Each of the state
Markov process
In probability theory and statistics, a Markov process, named after the Russian mathematician Andrey Markov, is a time-varying random phenomenon for which a specific property holds...
s of the Markov process represents one of the phases.
It has a discrete time
Discrete time
Discrete time is the discontinuity of a function's time domain that results from sampling a variable at a finite interval. For example, consider a newspaper that reports the price of crude oil once every day at 6:00AM. The newspaper is described as sampling the cost at a frequency of once per 24...
equivalent the discrete phase-type distribution
Discrete phase-type distribution
The discrete phase-type distribution is a probability distribution that results from a system of one or more inter-related geometric distributions occurring in sequence, or phases. The sequence in which each of the phases occur may itself be a stochastic process...
.
The set of phase-type distributions is dense in the field of all positive-valued distributions, that is, it can be used to approximate any positive valued distribution.
Definition
Consider a continuous-time Markov process with m+1 states, where m ≥ 1, such that the states 1,...,m are transient states and state 0 is an absorbing state. Further, let the process have an initial probability of starting in any of the m+1 phases given by the probability vector (α0,α).The continuous phase-type distribution is the distribution of time from the above process's starting until absorption in the absorbing state.
This process can be written in the form of a transition rate matrix,
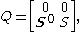
where S is an m×m matrix and S0 = -S1. Here 1 represents an m×1 vector with every element being 1.
Characterization
The distribution of time X until the process reaches the absorbing state is said to be phase-type distributed and is denoted PH(α,S).The distribution function of X is given by,
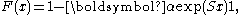
and the density function,
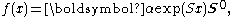
for all x > 0, where exp( · ) is the matrix exponential
Matrix exponential
In mathematics, the matrix exponential is a matrix function on square matrices analogous to the ordinary exponential function. Abstractly, the matrix exponential gives the connection between a matrix Lie algebra and the corresponding Lie group....
. It is usually assumed the probability of process starting in the absorbing state is zero. The moments of the distribution function are given by
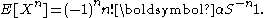
Special cases
The following probability distributions are all considered special cases of a continuous phase-type distribution:- Degenerate distribution, point mass at zero or the empty phase-type distribution - 0 phases.
- Exponential distributionExponential distributionIn probability theory and statistics, the exponential distribution is a family of continuous probability distributions. It describes the time between events in a Poisson process, i.e...
- 1 phase. - Erlang distribution - 2 or more identical phases in sequence.
- Deterministic distribution (or constant) - The limiting case of an Erlang distribution, as the number of phases become infinite, while the time in each state becomes zero.
- Coxian distribution - 2 or more (not necessarily identical) phases in sequence, with a probability of transitioning to the terminating/absorbing state after each phase.
- Hyper-exponential distribution (also called a mixture of exponential) - 2 or more non-identical phases, that each have a probability of occurring in a mutually exclusive, or parallel, manner. (Note: The exponential distribution is the degenerate situation when all the parallel phases are identical.)
- Hypoexponential distributionHypoexponential distributionIn probability theory the hypoexponential distribution or the generalized Erlang distribution is a continuous distribution, that has found use in the same fields as the Erlang distribution, such as queueing theory, teletraffic engineering and more generally in stochastic processes...
- 2 or more phases in sequence, can be non-identical or a mixture of identical and non-identical phases, generalises the Erlang.
As the phase-type distribution is dense in the field of all positive-valued distributions, we can represent any positive valued distribution. However, the phase-type is a light-tailed or platikurtic distribution. So the representation of heavy-tailed or leptokurtic distribution by phase type is an approximation, even if the precision of the approximation can be as good as we want.
Examples
In all the following examples it is assumed that there is no probability mass at zero, that is α0 = 0.Exponential distribution
The simplest non-trivial example of a phase-type distribution is the exponential distribution of parameter λ. The parameter of the phase-type distribution are : S = -λ and α = 1.Hyper-exponential or mixture of exponential distribution
The mixture of exponential or hyper-exponential distribution with λ1,λ2,...,λn>0 can be represented as a phase type distribution with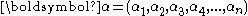
with
 and
and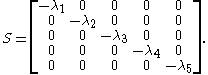
This mixture of densities of exponential distributed random variables can be characterized through
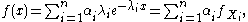
or its cumulative distribution function
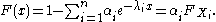
with
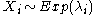
Erlang distribution
The Erlang distribution has two parameters, the shape an integer k > 0 and the rate λ > 0. This is sometimes denoted E(k,λ). The Erlang distribution can be written in the form of a phase-type distribution by making S a k×k matrix with diagonal elements -λ and super-diagonal elements λ, with the probability of starting in state 1 equal to 1. For example E(5,λ),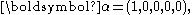
and
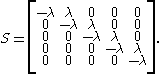
The hypoexponential distribution
Hypoexponential distribution
In probability theory the hypoexponential distribution or the generalized Erlang distribution is a continuous distribution, that has found use in the same fields as the Erlang distribution, such as queueing theory, teletraffic engineering and more generally in stochastic processes...
is a generalisation of the Erlang distribution by having different rates for each transition (the non-homogeneous case).
Mixture of Erlang distribution
The mixture of two Erlang distribution with parameter E(3,β1), E(3,β2) and (α1,α2) (such that α1 + α2 = 1 and for each i, αi ≥ 0) can be represented as a phase type distribution with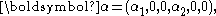
and
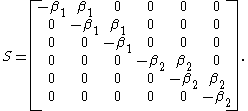
Coxian distribution
The Coxian distribution is a generalisation of the hypoexponential. Instead of only being able to enter the absorbing state from state k it can be reached from any phase. The phase-type representation is given by,
and
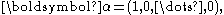
where 0 < p1,...,pk-1 ≤ 1. In the case where all pi = 1 we have the hypoexponential distribution. The Coxian distribution is extremely important as any acyclic phase-type distribution has an equivalent Coxian representation.
The generalised Coxian distribution relaxes the condition that requires starting in the first phase.
See also
- Discrete phase-type distributionDiscrete phase-type distributionThe discrete phase-type distribution is a probability distribution that results from a system of one or more inter-related geometric distributions occurring in sequence, or phases. The sequence in which each of the phases occur may itself be a stochastic process...
- Continuous-time Markov process
- Exponential distributionExponential distributionIn probability theory and statistics, the exponential distribution is a family of continuous probability distributions. It describes the time between events in a Poisson process, i.e...
- Hyper-exponential distribution
- Queueing modelQueueing modelIn queueing theory, a queueing model is used to approximate a real queueing situation or system, so the queueing behaviour can be analysed mathematically...
- Queueing theoryQueueing theoryQueueing theory is the mathematical study of waiting lines, or queues. The theory enables mathematical analysis of several related processes, including arriving at the queue, waiting in the queue , and being served at the front of the queue...

