Wigner semicircle distribution
Encyclopedia
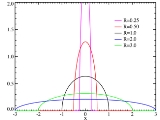
The Wigner semicircle distribution, named after the physicist Eugene Wigner, is the probability distribution
supported on the interval [−R, R] the graph of whose probability density function
f is a semicircle of radius R centered at (0, 0) and then suitably normalized
(so that it is really a semi-ellipse):
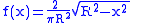
for −R < x < R, and f(x) = 0 if x > R or x < − R.
This distribution arises as the limiting distribution of eigenvalues of many random symmetric matrices as the size of the matrix approaches infinity.
It is a scaled beta distribution, more precisely, if Y is beta distributed with parameters α = β = 3/2, then X = 2RY – R has the above Wigner semicircle distribution.
of the second kind are orthogonal polynomials
with respect to the Wigner semicircle distribution.
For positive integers n, the 2n-th moment
of this distribution is
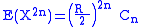
where X is any random variable with this distribution and Cn is the nth Catalan number
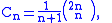
so that the moments are the Catalan numbers if R = 2. (Because of symmetry, all of the odd-order moments are zero.)
Making the substitution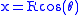 into the defining equation for the moment generating function it can be seen that:
into the defining equation for the moment generating function it can be seen that:

which can be solved (see Abramowitz and Stegun §9.6.18)
to yield:
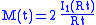
where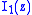 is the modified Bessel function
is the modified Bessel function
. Similarly, the characteristic function is given by:

where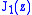 is the Bessel function. (See Abramowitz and Stegun §9.1.20), noting that the corresponding integral involving
is the Bessel function. (See Abramowitz and Stegun §9.1.20), noting that the corresponding integral involving 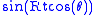 is zero.)
is zero.)
In the limit of approaching zero, the Wigner semicircle distribution becomes a Dirac delta function
approaching zero, the Wigner semicircle distribution becomes a Dirac delta function
.
theory, the role of Wigner's semicircle distribution is analogous to that of the normal distribution in classical probability theory. Namely,
in free probability theory, the role of cumulant
s is occupied by "free cumulants", whose relation to ordinary cumulants is simply that the role of the set of all partitions of a finite set
in the theory of ordinary cumulants is replaced by the set of all noncrossing partition
s of a finite set. Just the cumulants of degree more than 2 of a probability distribution
are all zero if and only if
the distribution is normal, so also, the free cumulants of degree more than 2 of a probability distribution are all zero if and only if the distribution is Wigner's semicircle distribution.
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
supported on the interval [−R, R] the graph of whose probability density function
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
f is a semicircle of radius R centered at (0, 0) and then suitably normalized
Normalizing constant
The concept of a normalizing constant arises in probability theory and a variety of other areas of mathematics.-Definition and examples:In probability theory, a normalizing constant is a constant by which an everywhere non-negative function must be multiplied so the area under its graph is 1, e.g.,...
(so that it is really a semi-ellipse):
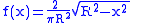
for −R < x < R, and f(x) = 0 if x > R or x < − R.
This distribution arises as the limiting distribution of eigenvalues of many random symmetric matrices as the size of the matrix approaches infinity.
It is a scaled beta distribution, more precisely, if Y is beta distributed with parameters α = β = 3/2, then X = 2RY – R has the above Wigner semicircle distribution.
General properties
The Chebyshev polynomialsChebyshev polynomials
In mathematics the Chebyshev polynomials, named after Pafnuty Chebyshev, are a sequence of orthogonal polynomials which are related to de Moivre's formula and which can be defined recursively. One usually distinguishes between Chebyshev polynomials of the first kind which are denoted Tn and...
of the second kind are orthogonal polynomials
Orthogonal polynomials
In mathematics, the classical orthogonal polynomials are the most widely used orthogonal polynomials, and consist of the Hermite polynomials, the Laguerre polynomials, the Jacobi polynomials together with their special cases the ultraspherical polynomials, the Chebyshev polynomials, and the...
with respect to the Wigner semicircle distribution.
For positive integers n, the 2n-th moment
Moment (mathematics)
In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...
of this distribution is
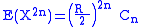
where X is any random variable with this distribution and Cn is the nth Catalan number
Catalan number
In combinatorial mathematics, the Catalan numbers form a sequence of natural numbers that occur in various counting problems, often involvingrecursively defined objects...
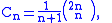
so that the moments are the Catalan numbers if R = 2. (Because of symmetry, all of the odd-order moments are zero.)
Making the substitution
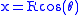 into the defining equation for the moment generating function it can be seen that:
into the defining equation for the moment generating function it can be seen that:
which can be solved (see Abramowitz and Stegun §9.6.18)
to yield:
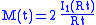
where
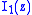 is the modified Bessel function
is the modified Bessel functionBessel function
In mathematics, Bessel functions, first defined by the mathematician Daniel Bernoulli and generalized by Friedrich Bessel, are canonical solutions y of Bessel's differential equation:...
. Similarly, the characteristic function is given by:

where
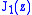 is the Bessel function. (See Abramowitz and Stegun §9.1.20), noting that the corresponding integral involving
is the Bessel function. (See Abramowitz and Stegun §9.1.20), noting that the corresponding integral involving 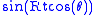 is zero.)
is zero.)In the limit of
 approaching zero, the Wigner semicircle distribution becomes a Dirac delta function
approaching zero, the Wigner semicircle distribution becomes a Dirac delta functionDirac delta function
The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
.
Relation to free probability
In free probabilityFree probability
Free probability is a mathematical theory that studies non-commutative random variables. The "freeness" or free independence property is the analogue of the classical notion of independence, and it is connected with free products....
theory, the role of Wigner's semicircle distribution is analogous to that of the normal distribution in classical probability theory. Namely,
in free probability theory, the role of cumulant
Cumulant
In probability theory and statistics, the cumulants κn of a probability distribution are a set of quantities that provide an alternative to the moments of the distribution. The moments determine the cumulants in the sense that any two probability distributions whose moments are identical will have...
s is occupied by "free cumulants", whose relation to ordinary cumulants is simply that the role of the set of all partitions of a finite set
Partition of a set
In mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
in the theory of ordinary cumulants is replaced by the set of all noncrossing partition
Noncrossing partition
In combinatorial mathematics, the topic of noncrossing partitions has assumed some importance because of its application to the theory of free probability...
s of a finite set. Just the cumulants of degree more than 2 of a probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
are all zero if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
the distribution is normal, so also, the free cumulants of degree more than 2 of a probability distribution are all zero if and only if the distribution is Wigner's semicircle distribution.
See also
- The W.s.d. is the limit of the Kesten–McKay distributions, as the parameter d tends to infinity.
- In number-theoreticNumber theoryNumber theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
literature, the Wigner distribution is sometimes called the Sato–Tate distribution. See Sato–Tate conjecture. - Marchenko–Pastur distributionMarchenko–Pastur distributionIn random matrix theory, the Marchenko–Pastur distribution, or Marchenko–Pastur law, describes the asymptotic behavior of singular values of large rectangular random matrices...
or Free Poisson distributionFree Poisson distributionIn the mathematics of free probability theory, the free Poisson distribution is a counterpart of the Poisson distribution in conventional probability theory.Definition....
External links
- Eric W. WeissteinEric W. WeissteinEric W. Weisstein is an encyclopedist who created and maintains MathWorld and Eric Weisstein's World of Science . He currently works for Wolfram Research, Inc.-Education:...
et al., Wigner's semicircle

