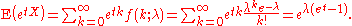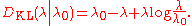
Poisson distribution
Encyclopedia
In probability theory
and statistics
, the Poisson distribution (or Poisson law of small numbers) is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time and/or space if these events occur with a known average rate and independently
of the time since the last event. (The Poisson distribution can also be used for the number of events in other specified intervals such as distance, area or volume.)
(1781–1840) and published, together with his probability theory, in 1837 in his work Recherches sur la probabilité des jugements en matière criminelle et en matière civile (“Research on the Probability of Judgments in Criminal and Civil Matters”). The work focused on certain random variable
s N that count, among other things, the number of discrete occurrences (sometimes called “arrivals”) that take place during a time
-interval of given length.
The first practical application of this distribution was done by Ladislaus Bortkiewicz
in 1898 when he was given the task to investigate the number of soldiers of the Prussian army killed accidentally by horse kick; this experiment introduced Poisson distribution to the field of reliability engineering
.
A classic example of Poisson distribution is the nuclear decay of atoms
. The decay of a radioactive sample is a case in point because, once a particle decays, it does not
decay again.
of occurrences in a given interval is λ, then the probability that there are exactly k occurrences (k being a non-negative integer
, k = 0, 1, 2, ...) is equal to

where
As a function of k, this is the probability mass function
. The Poisson distribution can be derived as a limiting case of the binomial distribution.
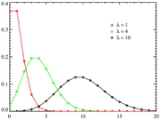
The Poisson distribution can be applied to systems with a large number of possible events, each of which is rare. The Poisson distribution is sometimes called a Poissonian.
number of occurrences , but also its variance
, but also its variance
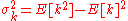 (see Table). Thus, the number of observed occurrences fluctuates about its mean λ with a standard deviation
(see Table). Thus, the number of observed occurrences fluctuates about its mean λ with a standard deviation
 . These fluctuations are denoted as Poisson noise or (particularly in electronics) as shot noise
. These fluctuations are denoted as Poisson noise or (particularly in electronics) as shot noise
.
The correlation of the mean and standard deviation in counting independent discrete occurrences is useful scientifically. By monitoring how the fluctuations vary with the mean signal, one can estimate the contribution of a single occurrence, even if that contribution is too small to be detected directly. For example, the charge e on an electron can be estimated by correlating the magnitude of an electric current
with its shot noise
. If N electrons pass a point in a given time t on the average, the mean
current
is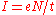 ; since the current fluctuations should be of the order
; since the current fluctuations should be of the order  (i.e., the standard deviation of the Poisson process
(i.e., the standard deviation of the Poisson process
), the charge can be estimated from the ratio
can be estimated from the ratio 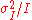 . An everyday example is the graininess that appears as photographs are enlarged; the graininess is due to Poisson fluctuations in the number of reduced silver
. An everyday example is the graininess that appears as photographs are enlarged; the graininess is due to Poisson fluctuations in the number of reduced silver
grains, not to the individual grains themselves. By correlating
the graininess with the degree of enlargement, one can estimate the contribution of an individual grain (which is otherwise too small to be seen unaided). Many other molecular applications of Poisson noise have been developed, e.g., estimating the number density of receptor
molecules in a cell membrane
.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
and statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the Poisson distribution (or Poisson law of small numbers) is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time and/or space if these events occur with a known average rate and independently
Statistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
of the time since the last event. (The Poisson distribution can also be used for the number of events in other specified intervals such as distance, area or volume.)
History
The distribution was first introduced by Siméon Denis PoissonSiméon Denis Poisson
Siméon Denis Poisson , was a French mathematician, geometer, and physicist. He however, was the final leading opponent of the wave theory of light as a member of the elite l'Académie française, but was proven wrong by Augustin-Jean Fresnel.-Biography:...
(1781–1840) and published, together with his probability theory, in 1837 in his work Recherches sur la probabilité des jugements en matière criminelle et en matière civile (“Research on the Probability of Judgments in Criminal and Civil Matters”). The work focused on certain random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s N that count, among other things, the number of discrete occurrences (sometimes called “arrivals”) that take place during a time
Time
Time is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....
-interval of given length.
The first practical application of this distribution was done by Ladislaus Bortkiewicz
Ladislaus Bortkiewicz
Ladislaus Josephovich Bortkiewicz , August 7, 1868 – July 15, 1931) was a Russian economist and statistician of Polish descent, who lived most of his professional life in Germany, where he taught at Strassburg University and Berlin University...
in 1898 when he was given the task to investigate the number of soldiers of the Prussian army killed accidentally by horse kick; this experiment introduced Poisson distribution to the field of reliability engineering
Reliability engineering
Reliability engineering is an engineering field, that deals with the study, evaluation, and life-cycle management of reliability: the ability of a system or component to perform its required functions under stated conditions for a specified period of time. It is often measured as a probability of...
.
Applications
Applications of Poisson distribution can be found in every field related to counting:- Electrical system example: telephone calls arriving in a system.
- AstronomyAstronomyAstronomy is a natural science that deals with the study of celestial objects and phenomena that originate outside the atmosphere of Earth...
example: photons arriving at a telescope. - BiologyBiologyBiology is a natural science concerned with the study of life and living organisms, including their structure, function, growth, origin, evolution, distribution, and taxonomy. Biology is a vast subject containing many subdivisions, topics, and disciplines...
example: the number of mutations on a given strand of DNADNADeoxyribonucleic acid is a nucleic acid that contains the genetic instructions used in the development and functioning of all known living organisms . The DNA segments that carry this genetic information are called genes, but other DNA sequences have structural purposes, or are involved in...
.
A classic example of Poisson distribution is the nuclear decay of atoms
Radioactive decay
Radioactive decay is the process by which an atomic nucleus of an unstable atom loses energy by emitting ionizing particles . The emission is spontaneous, in that the atom decays without any physical interaction with another particle from outside the atom...
. The decay of a radioactive sample is a case in point because, once a particle decays, it does not
decay again.
The distribution equation
If the expected numberExpected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
of occurrences in a given interval is λ, then the probability that there are exactly k occurrences (k being a non-negative integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
, k = 0, 1, 2, ...) is equal to

where
- e is the base of the natural logarithmE (mathematical constant)The mathematical constant ' is the unique real number such that the value of the derivative of the function at the point is equal to 1. The function so defined is called the exponential function, and its inverse is the natural logarithm, or logarithm to base...
(e = 2.71828...) - k is the number of occurrences of an event — the probability of which is given by the function
- k! is the factorialFactorialIn mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
of k - λ is a positive real numberReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
, equal to the expected numberExpected valueIn probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
of occurrences during the given interval. For instance, if the events occur on average 4 times per minuteMinuteA minute is a unit of measurement of time or of angle. The minute is a unit of time equal to 1/60th of an hour or 60 seconds. In the UTC time scale, a minute on rare occasions has 59 or 61 seconds; see leap second. The minute is not an SI unit; however, it is accepted for use with SI units...
, and one is interested in the probability of an event occurring k times in a 10 minute interval, one would use a Poisson distribution as the model with λ = 10×4 = 40.
As a function of k, this is the probability mass function
Probability mass function
In probability theory and statistics, a probability mass function is a function that gives the probability that a discrete random variable is exactly equal to some value...
. The Poisson distribution can be derived as a limiting case of the binomial distribution.
The Poisson distribution can be applied to systems with a large number of possible events, each of which is rare. The Poisson distribution is sometimes called a Poissonian.
Poisson noise and characterizing small occurrences
The parameter λ is not only the meanMean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
number of occurrences
 , but also its variance
, but also its varianceVariance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
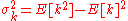 (see Table). Thus, the number of observed occurrences fluctuates about its mean λ with a standard deviation
(see Table). Thus, the number of observed occurrences fluctuates about its mean λ with a standard deviationStandard deviation
Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
 . These fluctuations are denoted as Poisson noise or (particularly in electronics) as shot noise
. These fluctuations are denoted as Poisson noise or (particularly in electronics) as shot noiseShot noise
Shot noise is a type of electronic noise that may be dominant when the finite number of particles that carry energy is sufficiently small so that uncertainties due to the Poisson distribution, which describes the occurrence of independent random events, are of significance...
.
The correlation of the mean and standard deviation in counting independent discrete occurrences is useful scientifically. By monitoring how the fluctuations vary with the mean signal, one can estimate the contribution of a single occurrence, even if that contribution is too small to be detected directly. For example, the charge e on an electron can be estimated by correlating the magnitude of an electric current
Electric current
Electric current is a flow of electric charge through a medium.This charge is typically carried by moving electrons in a conductor such as wire...
with its shot noise
Shot noise
Shot noise is a type of electronic noise that may be dominant when the finite number of particles that carry energy is sufficiently small so that uncertainties due to the Poisson distribution, which describes the occurrence of independent random events, are of significance...
. If N electrons pass a point in a given time t on the average, the mean
Mean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
current
Electric current
Electric current is a flow of electric charge through a medium.This charge is typically carried by moving electrons in a conductor such as wire...
is
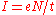 ; since the current fluctuations should be of the order
; since the current fluctuations should be of the order  (i.e., the standard deviation of the Poisson process
(i.e., the standard deviation of the Poisson processPoisson process
A Poisson process, named after the French mathematician Siméon-Denis Poisson , is a stochastic process in which events occur continuously and independently of one another...
), the charge
 can be estimated from the ratio
can be estimated from the ratio 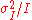 . An everyday example is the graininess that appears as photographs are enlarged; the graininess is due to Poisson fluctuations in the number of reduced silver
. An everyday example is the graininess that appears as photographs are enlarged; the graininess is due to Poisson fluctuations in the number of reduced silverSilver
Silver is a metallic chemical element with the chemical symbol Ag and atomic number 47. A soft, white, lustrous transition metal, it has the highest electrical conductivity of any element and the highest thermal conductivity of any metal...
grains, not to the individual grains themselves. By correlating
Correlation
In statistics, dependence refers to any statistical relationship between two random variables or two sets of data. Correlation refers to any of a broad class of statistical relationships involving dependence....
the graininess with the degree of enlargement, one can estimate the contribution of an individual grain (which is otherwise too small to be seen unaided). Many other molecular applications of Poisson noise have been developed, e.g., estimating the number density of receptor
Receptor (biochemistry)
In biochemistry, a receptor is a molecule found on the surface of a cell, which receives specific chemical signals from neighbouring cells or the wider environment within an organism...
molecules in a cell membrane
Cell membrane
The cell membrane or plasma membrane is a biological membrane that separates the interior of all cells from the outside environment. The cell membrane is selectively permeable to ions and organic molecules and controls the movement of substances in and out of cells. It basically protects the cell...
.
-
Related distributions
- If
 and
and  are independent, then the difference
are independent, then the difference 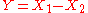 follows a Skellam distribution.
follows a Skellam distribution. - If
 and
and  are independent, and
are independent, and 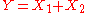 , then the distribution of
, then the distribution of  conditional on
conditional on  is a binomial. Specifically,
is a binomial. Specifically, 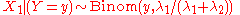 . More generally, if X1, X2,..., Xn are independent Poisson random variables with parameters λ1, λ2,..., λn then
. More generally, if X1, X2,..., Xn are independent Poisson random variables with parameters λ1, λ2,..., λn then
-
-

- The Poisson distribution can be derived as a limiting case to the binomial distribution as the number of trials goes to infinity and the expectedExpected valueIn probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
number of successes remains fixed — see law of rare events below. Therefore it can be used as an approximation of the binomial distribution if n is sufficiently large and p is sufficiently small. There is a rule of thumb stating that the Poisson distribution is a good approximation of the binomial distribution if n is at least 20 and p is smaller than or equal to 0.05, and an excellent approximation if n ≥ 100 and np ≤ 10. - For sufficiently large values of λ, (say λ>1000), the normal distribution with mean λ and variance λ (standard deviation
 ), is an excellent approximation to the Poisson distribution. If λ is greater than about 10, then the normal distribution is a good approximation if an appropriate continuity correctionContinuity correctionIn probability theory, if a random variable X has a binomial distribution with parameters n and p, i.e., X is distributed as the number of "successes" in n independent Bernoulli trials with probability p of success on each trial, then...
), is an excellent approximation to the Poisson distribution. If λ is greater than about 10, then the normal distribution is a good approximation if an appropriate continuity correctionContinuity correctionIn probability theory, if a random variable X has a binomial distribution with parameters n and p, i.e., X is distributed as the number of "successes" in n independent Bernoulli trials with probability p of success on each trial, then...
is performed, i.e., P(X ≤ x), where (lower-case) x is a non-negative integer, is replaced by P(X ≤ x + 0.5).
- The Poisson distribution can be derived as a limiting case to the binomial distribution as the number of trials goes to infinity and the expected
-

- Variance-stabilizing transformationVariance-stabilizing transformationIn applied statistics, a variance-stabilizing transformation is a data transformation that is specifically chosen either to simplify considerations in graphical exploratory data analysis or to allow the application of simple regression-based or analysis of variance techniques.The aim behind the...
: When a variable is Poisson distributed, its square root is approximately normally distributed with expected value of about and variance of about 1/4. Under this transformation, the convergence to normality is far faster than the untransformed variable. Other, slightly more complicated, variance stabilizing transformations are available, one of which is Anscombe transformAnscombe transformIn statistics, the Anscombe transform, named after Francis Anscombe, is a variance-stabilizing transformation that transforms a random variable with a Poisson distribution into one with an approximately standard Gaussian distribution. The Anscombe transform is widely used in photon-limited imaging ...
and variance of about 1/4. Under this transformation, the convergence to normality is far faster than the untransformed variable. Other, slightly more complicated, variance stabilizing transformations are available, one of which is Anscombe transformAnscombe transformIn statistics, the Anscombe transform, named after Francis Anscombe, is a variance-stabilizing transformation that transforms a random variable with a Poisson distribution into one with an approximately standard Gaussian distribution. The Anscombe transform is widely used in photon-limited imaging ...
. See Data transformation (statistics)Data transformation (statistics)In statistics, data transformation refers to the application of a deterministic mathematical function to each point in a data set — that is, each data point zi is replaced with the transformed value yi = f, where f is a function...
for more general uses of transformations. - If the number of arrivals in any given time interval
 follows the Poisson distribution, with mean =
follows the Poisson distribution, with mean =  , then the lengths of the inter-arrival times follow the Exponential distributionExponential distributionIn probability theory and statistics, the exponential distribution is a family of continuous probability distributions. It describes the time between events in a Poisson process, i.e...
, then the lengths of the inter-arrival times follow the Exponential distributionExponential distributionIn probability theory and statistics, the exponential distribution is a family of continuous probability distributions. It describes the time between events in a Poisson process, i.e...
, with mean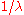 .
.
- Variance-stabilizing transformation
-
Occurrence
The Poisson distribution arises in connection with Poisson processPoisson processA Poisson process, named after the French mathematician Siméon-Denis Poisson , is a stochastic process in which events occur continuously and independently of one another...
es. It applies to various phenomena of discrete properties (that is, those that may happen 0, 1, 2, 3, ... times during a given period of time or in a given area) whenever the probability of the phenomenon happening is constant in time or spaceSpaceSpace is the boundless, three-dimensional extent in which objects and events occur and have relative position and direction. Physical space is often conceived in three linear dimensions, although modern physicists usually consider it, with time, to be part of a boundless four-dimensional continuum...
. Examples of events that may be modelled as a Poisson distribution include:
- The number of soldiers killed by horse-kicks each year in each corps in the PrussiaPrussiaPrussia was a German kingdom and historic state originating out of the Duchy of Prussia and the Margraviate of Brandenburg. For centuries, the House of Hohenzollern ruled Prussia, successfully expanding its size by way of an unusually well-organized and effective army. Prussia shaped the history...
n cavalry. This example was made famous by a book of Ladislaus Josephovich BortkiewiczLadislaus BortkiewiczLadislaus Josephovich Bortkiewicz , August 7, 1868 – July 15, 1931) was a Russian economist and statistician of Polish descent, who lived most of his professional life in Germany, where he taught at Strassburg University and Berlin University...
(1868–1931). - The number of yeast cells used when brewing GuinnessGuinnessGuinness is a popular Irish dry stout that originated in the brewery of Arthur Guinness at St. James's Gate, Dublin. Guinness is directly descended from the porter style that originated in London in the early 18th century and is one of the most successful beer brands worldwide, brewed in almost...
beer. This example was made famous by William Sealy GossetWilliam Sealy GossetWilliam Sealy Gosset is famous as a statistician, best known by his pen name Student and for his work on Student's t-distribution....
(1876–1937). - The number of phone calls arriving at a call centreCall centreA call centre or call center is a centralised office used for the purpose of receiving and transmitting a large volume of requests by telephone. A call centre is operated by a company to administer incoming product support or information inquiries from consumers. Outgoing calls for telemarketing,...
per minute. - The number of goals in sports involving two competing teams.
- The number of deaths per year in a given age group.
- The number of jumps in a stock price in a given time interval.
- Under an assumption of homogeneity, the number of times a web serverWeb serverWeb server can refer to either the hardware or the software that helps to deliver content that can be accessed through the Internet....
is accessed per minute. - The number of mutationMutationIn molecular biology and genetics, mutations are changes in a genomic sequence: the DNA sequence of a cell's genome or the DNA or RNA sequence of a virus. They can be defined as sudden and spontaneous changes in the cell. Mutations are caused by radiation, viruses, transposons and mutagenic...
s in a given stretch of DNADNADeoxyribonucleic acid is a nucleic acid that contains the genetic instructions used in the development and functioning of all known living organisms . The DNA segments that carry this genetic information are called genes, but other DNA sequences have structural purposes, or are involved in...
after a certain amount of radiation. - The proportion of cells that will be infected at a given multiplicity of infectionMultiplicity of infectionThe multiplicity of infection or MOI is the ratio of infectious agents to infection targets . For example, when referring to a group of cells inoculated with infectious virus particles, the multiplicity of infection or MOI is the ratio of the number of infectious virus particles to the number of...
.
How does this distribution arise? — The law of rare events
In several of the above examples—such as, the number of mutations in a given sequence of DNA—the events being counted are actually the outcomes of discrete trials, and would more precisely be modelled using the binomial distribution, that is
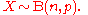
In such cases n is very large and p is very small (and so the expectation np is of intermediate magnitude). Then the distribution may be approximated by the less cumbersome Poisson distribution
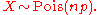
This is sometimes known as the law of rare events, since each of the n individual Bernoulli events rarely occurs. The name may be misleading because the total count of success events in a Poisson process need not be rare if the parameter np is not small. For example, the number of telephone calls to a busy switchboard in one hour follows a Poisson distribution with the events appearing frequent to the operator, but they are rare from the point of view of the average member of the population who is very unlikely to make a call to that switchboard in that hour.
Proof
We will prove that, for fixed , if
, if
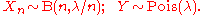
then for each fixed k
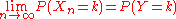 .
.
To see the connection with the above discussion, for any Binomial random variable with large n and small p set . Note that the expectation
. Note that the expectation 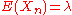 is fixed with respect to n.
is fixed with respect to n.
First, recall from calculusCalculusCalculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
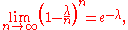
then since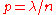 in this case, we have
in this case, we have
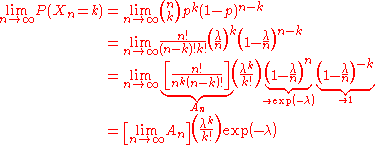
Next, note that
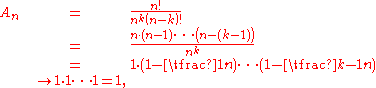
where we have taken the limit of each of the terms independently, which is permitted since there is a fixed number of terms with respect to n (there are k of them). Consequently, we have shown that
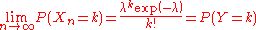 .
.
Generalization
We have shown that if

where , then
, then  in distribution. This holds in the more general situation that
in distribution. This holds in the more general situation that 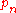 is any sequence such that
is any sequence such that
2-dimensional Poisson process
where- e is the base of the natural logarithmE (mathematical constant)The mathematical constant ' is the unique real number such that the value of the derivative of the function at the point is equal to 1. The function so defined is called the exponential function, and its inverse is the natural logarithm, or logarithm to base...
(e = 2.71828...) - k is the number of occurrences of an event - the probability of which is given by the function
- k! is the factorialFactorialIn mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
of k - D is the 2-dimensional region
- |D| is the area of the region
- N(D) is the number of points in the process in region D
Properties
- The expected valueExpected valueIn probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
of a Poisson-distributed random variable is equal to λ and so is its varianceVarianceIn probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
. The higher momentsMoment (mathematics)In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...
of the Poisson distribution are Touchard polynomials in λ, whose coefficients have a combinatorialCombinatoricsCombinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
meaning. In fact, when the expected value of the Poisson distribution is 1, then Dobinski's formula says that the nth moment equals the number of partitions of a setPartition of a setIn mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
of size n. - The modeMode (statistics)In statistics, the mode is the value that occurs most frequently in a data set or a probability distribution. In some fields, notably education, sample data are often called scores, and the sample mode is known as the modal score....
of a Poisson-distributed random variable with non-integer λ is equal to , which is the largest integer less than or equal to λ. This is also written as floorFloor functionIn mathematics and computer science, the floor and ceiling functions map a real number to the largest previous or the smallest following integer, respectively...
, which is the largest integer less than or equal to λ. This is also written as floorFloor functionIn mathematics and computer science, the floor and ceiling functions map a real number to the largest previous or the smallest following integer, respectively...
(λ). When λ is a positive integer, the modes are λ and λ − 1. - Given one event (or any number) the expected number of other events is independent so still λ. If reproductive success follows a Poisson distribution with expected number of offspring λ, then for a given individual the expected number of (half)siblings (per parent) is also λ. If fullsiblings are rare total expected sibs are 2λ.
- Sums of Poisson-distributed random variables:
- If
 follow a Poisson distribution with parameter
follow a Poisson distribution with parameter 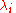 and
and 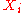 are independentStatistical independenceIn probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
are independentStatistical independenceIn probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
, then -
- also follows a Poisson distribution whose parameter is the sum of the component parameters. A converse is Raikov's theoremRaikov's theoremIn probability theory, Raikov’s theorem, named after Dmitry Raikov, states that if the sum of two independent random variables X and Y has a Poisson distribution, then both X and Y themselves must have the Poisson distribution. It says the same thing about the Poisson distribution that Cramér's...
, which says that if the sum of two independent random variables is Poisson-distributed, then so is each of those two independent random variables.- The sum of normalised square deviations is approximately distributed as chi-squaredChi-squaredIn statistics, the term chi-squared has different uses:*chi-squared distribution, a continuous probability distribution;*chi-squared statistic, a statistic used in some statistical tests;...
if the mean is of a moderate size ( is suggested). If
is suggested). If  are observations from independent Poisson distributions with means
are observations from independent Poisson distributions with means  then
then 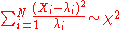
- The moment-generating functionMoment-generating functionIn probability theory and statistics, the moment-generating function of any random variable is an alternative definition of its probability distribution. Thus, it provides the basis of an alternative route to analytical results compared with working directly with probability density functions or...
of the Poisson distribution with expected value λ is
- The sum of normalised square deviations is approximately distributed as chi-squared
- All of the cumulantCumulantIn probability theory and statistics, the cumulants κn of a probability distribution are a set of quantities that provide an alternative to the moments of the distribution. The moments determine the cumulants in the sense that any two probability distributions whose moments are identical will have...
s of the Poisson distribution are equal to the expected value λ. The nth factorial moment of the Poisson distribution is λn. - The Poisson distributions are infinitely divisibleInfinite divisibility (probability)The concepts of infinite divisibility and the decomposition of distributions arise in probability and statistics in relation to seeking families of probability distributions that might be a natural choice in certain applications, in the same way that the normal distribution is...
probability distributions. - The directed Kullback-Leibler divergence between Pois(λ) and Pois(λ0) is given by
- Upper bound for the tail probability of a Poisson random variable
 . The proof uses a Chernoff boundChernoff boundIn probability theory, the Chernoff bound, named after Herman Chernoff, gives exponentially decreasing bounds on tail distributions of sums of independent random variables...
. The proof uses a Chernoff boundChernoff boundIn probability theory, the Chernoff bound, named after Herman Chernoff, gives exponentially decreasing bounds on tail distributions of sums of independent random variables...
argument.
- Similarly,
Evaluating the Poisson Distribution
Although the Poisson distribution is limited by ,
,
the numerator and denominator of can reach
can reach
extreme values for large values of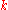 or
or 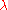 .
.
If the Poisson distribution is evaluated on a computer with limited
precision by first evaluating its numerator and denominator and then
dividing the two, then a significant loss of precisionPrecision (computer science)In computer science, precision of a numerical quantity is a measure of the detail in which the quantity is expressed. This is usually measured in bits, but sometimes in decimal digits. It is related to precision in mathematics, which describes the number of digits that are used to express a...
may occur.
For example, with the common double precision
a complete loss of precision occurs if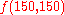 is evaluated in this manner.
is evaluated in this manner.
A more robustNumerical stabilityIn the mathematical subfield of numerical analysis, numerical stability is a desirable property of numerical algorithms. The precise definition of stability depends on the context, but it is related to the accuracy of the algorithm....
evaluation method is: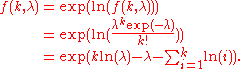
Generating Poisson-distributed random variables
A simple algorithm to generate random Poisson-distributed numbers (pseudo-random number samplingPseudo-random number samplingPseudo-random number sampling or non-uniform pseudo-random variate generation is the numerical practice of generating pseudo-random numbers that are distributed according to a given probability distribution....
) has been given by KnuthDonald KnuthDonald Ervin Knuth is a computer scientist and Professor Emeritus at Stanford University.He is the author of the seminal multi-volume work The Art of Computer Programming. Knuth has been called the "father" of the analysis of algorithms...
(see References below):
algorithm poisson random number (Knuth):
init:
Let L ← e−λ, k ← 0 and p ← 1.
do:
k ← k + 1.
Generate uniform random number u in [0,1] and let p ← p × u.
while p > L.
return k − 1.
While simple, the complexity is linear in λ. There are many other algorithms to overcome this. Some are given in Ahrens & Dieter, see References below. Also, for large values of λ, there may be numerical stability issues because of the term e−λ. One solution for large values of λ is Rejection samplingRejection samplingIn mathematics, rejection sampling is a basic pseudo-random number sampling technique used to generate observations from a distribution. It is also commonly called the acceptance-rejection method or "accept-reject algorithm"....
, another is to use a Gaussian approximation to the Poisson.
Inverse transform sampling is simple and efficient for small values of λ, and requires only one uniform random number u per sample. Cumulative probabilities are examined in turn until one exceeds u.
Maximum likelihood
Given a sample of n measured values ki we wish to estimate the value of the parameter λ of the Poisson population from which the sample was drawn. To calculate the maximum likelihoodMaximum likelihoodIn statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....
value, we form the log-likelihood function

Take the derivative of L with respect to λ and equate it to zero:
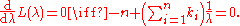
Solving for λ yields a stationary point, which if the second derivative is negative is the maximum-likelihood estimate of λ:
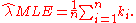
Checking the second derivative, it is found that it is negative for all λ and ki greater than zero, therefore this stationary point is indeed a maximum of the initial likelihood function: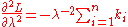
Since each observation has expectation λ so does this sample mean. Therefore it is an unbiased estimator of λ. It is also an efficient estimator, i.e. its estimation variance achieves the Cramér–Rao lower bound (CRLB). Hence it is MVUE. Also it can be proved that the sample mean is complete and sufficient statistic for λ.
Bayesian inference
In Bayesian inferenceBayesian inferenceIn statistics, Bayesian inference is a method of statistical inference. It is often used in science and engineering to determine model parameters, make predictions about unknown variables, and to perform model selection...
, the conjugate priorConjugate priorIn Bayesian probability theory, if the posterior distributions p are in the same family as the prior probability distribution p, the prior and posterior are then called conjugate distributions, and the prior is called a conjugate prior for the likelihood...
for the rate parameter λ of the Poisson distribution is the Gamma distribution. Let

denote that λ is distributed according to the Gamma densityProbability density functionIn probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
g parameterized in terms of a shape parameterShape parameterIn probability theory and statistics, a shape parameter is a kind of numerical parameter of a parametric family of probability distributions.- Definition :...
α and an inverse scale parameterScale parameterIn probability theory and statistics, a scale parameter is a special kind of numerical parameter of a parametric family of probability distributions...
β:
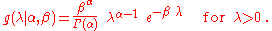
Then, given the same sample of n measured values ki as before, and a prior of Gamma(α, β), the posterior distribution is

The posterior mean E[λ] approaches the maximum likelihood estimate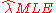 in the limit as
in the limit as  .
.
The posterior predictive distribution of additional data is a Gamma-Poisson (i.e. negative binomialNegative binomial distributionIn probability theory and statistics, the negative binomial distribution is a discrete probability distribution of the number of successes in a sequence of Bernoulli trials before a specified number of failures occur...
) distribution.
Confidence interval
A simple and rapid method to calculate an approximate confidence interval for the estimation of λ is proposed in Guerriero et al. (2009). This method provides a good approximation of the confidence interval limits, for samples containing at least 15 – 20 elements. Denoting by N the number of sampled points or events and by L the length of sample line (or the time interval), the upper and lower limits of the 95% confidence interval are given by:
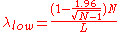
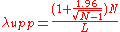
The "law of small numbers"
The word law is sometimes used as a synonym of probability distributionProbability distributionIn probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
, and convergence in law means convergence in distribution. Accordingly, the Poisson distribution is sometimes called the law of small numbers because it is the probability distribution of the number of occurrences of an event that happens rarely but has very many opportunities to happen. The Law of Small Numbers is a book by Ladislaus BortkiewiczLadislaus BortkiewiczLadislaus Josephovich Bortkiewicz , August 7, 1868 – July 15, 1931) was a Russian economist and statistician of Polish descent, who lived most of his professional life in Germany, where he taught at Strassburg University and Berlin University...
about the Poisson distribution, published in 1898. Some have suggested that the Poisson distribution should have been called the Bortkiewicz distribution.
See also
- Coefficient of dispersionCoefficient of dispersionIn probability theory and statistics, the index of dispersion, dispersion index, coefficient of dispersion, or variance-to-mean ratio , like the coefficient of variation, is a normalized measure of the dispersion of a probability distribution: it is a measure used to quantify whether a set of...
- Compound Poisson distributionCompound Poisson distributionIn probability theory, a compound Poisson distribution is the probability distribution of the sum of a "Poisson-distributed number" of independent identically-distributed random variables...
- Conway–Maxwell–Poisson distribution
- Dobinski's formula
- Erlang distribution
- Incomplete gamma functionIncomplete gamma functionIn mathematics, the gamma function is defined by a definite integral. The incomplete gamma function is defined as an integral function of the same integrand. There are two varieties of the incomplete gamma function: the upper incomplete gamma function is for the case that the lower limit of...
- Poisson processPoisson processA Poisson process, named after the French mathematician Siméon-Denis Poisson , is a stochastic process in which events occur continuously and independently of one another...
- Poisson regressionPoisson regressionIn statistics, Poisson regression is a form of regression analysis used to model count data and contingency tables. Poisson regression assumes the response variable Y has a Poisson distribution, and assumes the logarithm of its expected value can be modeled by a linear combination of unknown...
- Poisson samplingPoisson samplingIn the theory of finite population sampling, Poisson sampling is a sampling process where each element of the population that is sampled is subjected to an independent Bernoulli trial which determines whether the element becomes part of the sample during the drawing of a single sample.Each element...
- Queueing theoryQueueing theoryQueueing theory is the mathematical study of waiting lines, or queues. The theory enables mathematical analysis of several related processes, including arriving at the queue, waiting in the queue , and being served at the front of the queue...
- Renewal theoryRenewal theoryRenewal theory is the branch of probability theory that generalizes Poisson processes for arbitrary holding times. Applications include calculating the expected time for a monkey who is randomly tapping at a keyboard to type the word Macbeth and comparing the long-term benefits of different...
- Robbins lemmaRobbins lemmaIn statistics, the Robbins lemma, named after Herbert Robbins, states that if X is a random variable with a Poisson distribution, and f is any function for which the expected value E exists, then...
- Skellam distribution
- Tweedie distributionsTweedie distributionsIn probability and statistics, the Tweedie distributions are a family of probability distributions which include continuous distributions such as the normal and gamma, the purely discrete scaled Poisson distribution, and the class of mixed compound Poisson-Gamma distributions which have positive...
External links
- If