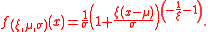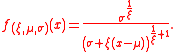Generalized Pareto distribution
Encyclopedia
The family of generalized Pareto distributions (GPD) has three parameters 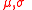 and
and 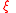 .
.
The cumulative distribution function
is
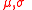 and
and 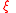 .
.The cumulative distribution function
Cumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
is
-

for when
when 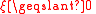 , and
, and 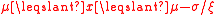 when
when  , where
, where 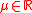 is the location parameter,
is the location parameter,  the scale parameter and
the scale parameter and  the shape parameter. Note that some references give the "shape parameter" as
the shape parameter. Note that some references give the "shape parameter" as 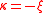 .
.
The probability density functionProbability density functionIn probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
is:
or
again, for , and
, and  when
when  .
.
Generating generalized Pareto random variables
If U is uniformly distributedUniform distribution (continuous)In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of probability distributions such that for each member of the family, all intervals of the same length on the distribution's support are equally probable. The support is defined by...
on
(0, 1] , then
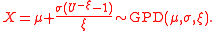
In Matlab Statistics Toolbox, you can easily use "gprnd" command to generate generalized Pareto random numbers.
With GNU R you can use the packages POT or evd with the "rgpd" command (see for exact usage: http://rss.acs.unt.edu/Rdoc/library/POT/html/simGPD.html) -