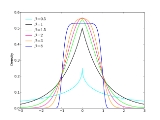
Generalized normal distribution
Encyclopedia
The generalized normal distribution or generalized Gaussian distribution is either of two families of parametric
continuous probability distributions on the real
line. Both families add a shape parameter
to the normal distribution. To distinguish the two families, they are referred to below as "version 1" and "version 2." However this is not a standard nomenclature.
This family includes the normal distribution when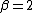 (with mean
(with mean 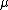 and variance
and variance 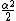 ) and it includes the Laplace distribution when
) and it includes the Laplace distribution when 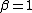 . As
. As 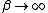 , the density converges pointwise
, the density converges pointwise
to a uniform density on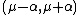 .
.
This family allows for tails that are either heavier than normal (when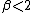 ) or lighter than normal (when
) or lighter than normal (when 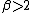 ). It is a useful way to parametrize a continuum of symmetric, platykurtic densities spanning from the normal (
). It is a useful way to parametrize a continuum of symmetric, platykurtic densities spanning from the normal (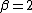 ) to the uniform density (
) to the uniform density (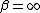 ), and a continuum of symmetric, leptokurtic densities spanning from the Laplace (
), and a continuum of symmetric, leptokurtic densities spanning from the Laplace (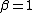 ) to the normal density (
) to the normal density ( ).
).
has been studied. The estimates do not have a closed form and must be obtained numerically. Estimators that do not require numerical calculation have also been proposed.
The generalized normal log-likelihood function has infinitely many continuous derivates (i.e. it belongs to the class C∞ of smooth function
s) only if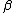 is a positive, even integer. Otherwise, the function has
is a positive, even integer. Otherwise, the function has 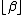 continuous derivatives. As a result, the standard results for consistency and asymptotic normality of maximum likelihood
continuous derivatives. As a result, the standard results for consistency and asymptotic normality of maximum likelihood
estimates of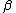 only apply when
only apply when 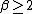 .
.
at the origin.
 exponential power distributions with the same
exponential power distributions with the same 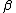 and
and  parameters, is the only probability density that can be written in the form
parameters, is the only probability density that can be written in the form  and has independent marginals. The results for the special case of the Multivariate normal distribution is originally attributed to Maxwell
and has independent marginals. The results for the special case of the Multivariate normal distribution is originally attributed to Maxwell
.
, and inverse normal distributions are defined as transformations of a normally-distributed value, but unlike the generalized normal and skew-normal families, these do not include the normal distributions as special cases.
Parametric statistics
Parametric statistics is a branch of statistics that assumes that the data has come from a type of probability distribution and makes inferences about the parameters of the distribution. Most well-known elementary statistical methods are parametric....
continuous probability distributions on the real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
line. Both families add a shape parameter
Shape parameter
In probability theory and statistics, a shape parameter is a kind of numerical parameter of a parametric family of probability distributions.- Definition :...
to the normal distribution. To distinguish the two families, they are referred to below as "version 1" and "version 2." However this is not a standard nomenclature.
Version 1
Known also as the exponential power distribution, or the generalized error distribution, this is a parametric family of symmetric distributions. It includes all normal and Laplace distributions, and as limiting cases it includes all continuous uniform distributions on bounded intervals of the real line.This family includes the normal distribution when
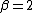 (with mean
(with mean 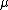 and variance
and variance 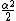 ) and it includes the Laplace distribution when
) and it includes the Laplace distribution when 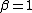 . As
. As 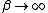 , the density converges pointwise
, the density converges pointwisePointwise convergence
In mathematics, pointwise convergence is one of various senses in which a sequence of functions can converge to a particular function.-Definition:...
to a uniform density on
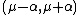 .
.This family allows for tails that are either heavier than normal (when
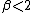 ) or lighter than normal (when
) or lighter than normal (when 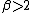 ). It is a useful way to parametrize a continuum of symmetric, platykurtic densities spanning from the normal (
). It is a useful way to parametrize a continuum of symmetric, platykurtic densities spanning from the normal (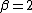 ) to the uniform density (
) to the uniform density (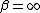 ), and a continuum of symmetric, leptokurtic densities spanning from the Laplace (
), and a continuum of symmetric, leptokurtic densities spanning from the Laplace (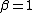 ) to the normal density (
) to the normal density ( ).
).Parameter estimation
Parameter estimation via maximum likelihood and the method of momentsMethod of moments
Method of moments may refer to:* Method of moments , a method of parameter estimation in statistics* Method of moments , a way of proving convergence in distribution in probability theory...
has been studied. The estimates do not have a closed form and must be obtained numerically. Estimators that do not require numerical calculation have also been proposed.
The generalized normal log-likelihood function has infinitely many continuous derivates (i.e. it belongs to the class C∞ of smooth function
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
s) only if
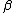 is a positive, even integer. Otherwise, the function has
is a positive, even integer. Otherwise, the function has 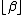 continuous derivatives. As a result, the standard results for consistency and asymptotic normality of maximum likelihood
continuous derivatives. As a result, the standard results for consistency and asymptotic normality of maximum likelihoodMaximum likelihood
In statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....
estimates of
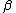 only apply when
only apply when 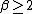 .
.Applications
This version of the generalized normal distribution has been used in modeling when the concentration of values around the mean and the tail behavior are of particular interest. Other families of distributions can be used if the focus is on other deviations from normality. If the symmetry of the distribution is the main interest, the skew normal family or version 2 of the generalized normal family discussed below can be used. If the tail behavior is the main interest, the student t family can be used, which approximates the normal distribution as the degrees of freedom grows to infinity. The t distribution, unlike this generalized normal distribution, obtains heavier than normal tails without acquiring a cuspCusp (singularity)
In the mathematical theory of singularities a cusp is a type of singular point of a curve. Cusps are local singularities in that they are not formed by self intersection points of the curve....
at the origin.
Properties
The multivariate generalized normal distribution, i.e. the product of exponential power distributions with the same
exponential power distributions with the same 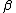 and
and  parameters, is the only probability density that can be written in the form
parameters, is the only probability density that can be written in the form  and has independent marginals. The results for the special case of the Multivariate normal distribution is originally attributed to Maxwell
and has independent marginals. The results for the special case of the Multivariate normal distribution is originally attributed to MaxwellJames Clerk Maxwell
James Clerk Maxwell of Glenlair was a Scottish physicist and mathematician. His most prominent achievement was formulating classical electromagnetic theory. This united all previously unrelated observations, experiments and equations of electricity, magnetism and optics into a consistent theory...
.
Version 2
This is a family of continuous probability distributions in which the shape parameter can be used to introduce skew. When the shape parameter is zero, the normal distribution results. Positive values of the shape parameter yield left-skewed distributions bounded to the right, and negative values of the shape parameter yield right-skewed distributions bounded to the left. Only when the shape parameter is zero is the density function for this distribution positive over the whole real line: in this case the distribution is a normal distribution, otherwise the distributions are shifted and possibly reversed log-normal distributions.Parameter estimation
Parameters can be estimated via maximum likelihood estimation or the method of moments. The parameter estimates do not have a closed form, so numerical calculations must be used to compute the estimates. Since the sample space (the set of real numbers where the density is non-zero) depends on the true value of the parameter, some standard results about the performance of parameter estimates will not automatically apply when working with this family.Applications
This family of distributions can be used to model values that may be normally distributed, or that may be either right-skewed or left-skewed relative to the normal distribution. The skew normal distribution is another distribution that is useful for modeling deviations from normality due to skew. Other distributions used to model skewed data include the gamma, lognormal, and Weilbull distributions, but these do not include the normal distributions as special cases.Other distributions related to the normal
The two generalized normal families described here, like the skew normal family, are parametric families that extends the normal distribution by adding a shape parameter. Due to the central role of the normal distribution in probability and statistics, many distributions can be characterized in terms of their relationship to the normal distribution. For example, the lognormal, folded normalFolded Normal Distribution
The folded normal distribution is a probability distribution related to the normal distribution. Given a normally distributed random variable X with mean μ and variance σ2, the random variable Y = |X| has a folded normal distribution. Such a case may be encountered if only the magnitude of some...
, and inverse normal distributions are defined as transformations of a normally-distributed value, but unlike the generalized normal and skew-normal families, these do not include the normal distributions as special cases.

