Rice distribution
Encyclopedia
In probability theory
, the Rice distribution or Rician distribution is the probability distribution
of the absolute value of a circular bivariate normal random variable with potentially non-zero mean. It was named after Stephen O. Rice
.
where I0(z) is the modified Bessel function
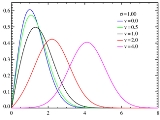
of the first kind with order zero. When v = 0, the distribution reduces to a Rayleigh distribution.
The characteristic function
is:
where
is one of Horn's confluent hypergeometric functions with two variables and convergent for all finite values of 
and 
. It is given by:
where
is the rising factorial.
where Lq(x) denotes a Laguerre polynomial
:
where
is the confluent hypergeometric function
of the first kind.
For the case q = 1/2:
Generally the moments are given by
where s = σ1/2.
When k is even, the moments become actual polynomials in σ and ν.
The second central moment
, equals the variance equation below (which is listed to the right):
Note that
indicates the square of the Laguerre polynomial 
, not the generalized Laguerre polynomial 
.
When the Rice distribution parameter ν = 0, the distribution becomes the Rayleigh distribution.
which is the variance of the Rayleigh distribution.
It is seen that as ν becomes large or σ becomes small the mean becomes ν and the variance becomes σ2.
Here the interest is in estimating the parameters of the distribution, ν and σ, from a sample of data. This can be done using the method of moments, e.g., the sample mean and the sample standard deviation. The sample mean is an estimate of μ1' and the sample standard deviation is an estimate of μ21/2.
The following is an efficient method, known as the "Koay inversion technique", published by Koay et al. for solving the estimating equations
, based on the sample mean and the sample standard deviation, simultaneously . This inversion technique is also known as the fixed point
formula of SNR. Earlier works on the method of moments usually use a root-finding method to solve the problem, which is not efficient.
First, the ratio of the sample mean to the sample standard deviation is defined as r, i.e.,
. The fixed point formula of SNR is expressed as
where
is the ratio of the parameters, i.e., 
, and 
is given by:
where
and 
are modified Bessel functions of the first kind.
Note that
is a scaling factor of 
and is related to 
by:
To find the fixed point,
, of 
, an initial solution is selected, 
, that is greater than the lower bound, which is 
and occurs when 
(Notice that this is the 
of a Rayleigh). This provides a starting point for the iteration, which uses functional composition, and this continues until 
is less than some small positive value. Here, 
denotes the composition of the same function, 
, 
-th times. In practice, we associate the final 
for some integer 
as the fixed point, 
, i.e., 
.
Once the fixed point is found, the estimates
and 
are found through the scaling function, 
, as follows:
,
and
.
To speed up the iteration even more, one can use the Newton's method of root-finding as presented by Koay et al. This particular approach is highly efficient.
The author has also provided an online calculator for computing the fixed point, which is also known as the underlying SNR from
, the magnitude SNR. See the link here under the subtitle called HI-SPEED SNR Analysis I. Note that the number of combined channel is 1 for the Rician distribution.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, the Rice distribution or Rician distribution is the probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
of the absolute value of a circular bivariate normal random variable with potentially non-zero mean. It was named after Stephen O. Rice
Stephen O. Rice
Stephen O. "Steve" Rice was a pioneer in the field of communication theory.-Biography:...
.
Characterization
The probability density function iswhere I0(z) is the modified Bessel function
Bessel function
In mathematics, Bessel functions, first defined by the mathematician Daniel Bernoulli and generalized by Friedrich Bessel, are canonical solutions y of Bessel's differential equation:...
of the first kind with order zero. When v = 0, the distribution reduces to a Rayleigh distribution.
The characteristic function
Characteristic function (probability theory)
In probability theory and statistics, the characteristic function of any random variable completely defines its probability distribution. Thus it provides the basis of an alternative route to analytical results compared with working directly with probability density functions or cumulative...
is:
where
is one of Horn's confluent hypergeometric functions with two variables and convergent for all finite values of and . It is given by:where
is the rising factorial.
Moments
The first few raw moments are:where Lq(x) denotes a Laguerre polynomial
Laguerre polynomials
In mathematics, the Laguerre polynomials, named after Edmond Laguerre ,are the canonical solutions of Laguerre's equation:x\,y + \,y' + n\,y = 0\,which is a second-order linear differential equation....
:
where
is the confluent hypergeometric functionConfluent hypergeometric function
In mathematics, a confluent hypergeometric function is a solution of a confluent hypergeometric equation, which is a degenerate form of a hypergeometric differential equation where two of the three regular singularities merge into an irregular singularity...
of the first kind.
For the case q = 1/2:
Generally the moments are given by
where s = σ1/2.
When k is even, the moments become actual polynomials in σ and ν.
The second central moment
Central moment
In probability theory and statistics, central moments form one set of values by which the properties of a probability distribution can be usefully characterised...
, equals the variance equation below (which is listed to the right):
Note that
indicates the square of the Laguerre polynomial , not the generalized Laguerre polynomial .When the Rice distribution parameter ν = 0, the distribution becomes the Rayleigh distribution.
which is the variance of the Rayleigh distribution.
Related distributions
has a Rice distribution if 
where 
and 
are statistically independent normal random variables and 
is any real number.
- Another case where
comes from the following steps:
- 1. Generate
having a Poisson distributionPoisson distributionIn probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time and/or space if these events occur with a known average rate and independently of the time since...
with parameter (also mean, for a Poisson)
- 2. Generate
having a chi-squared distribution with 2P + 2 degrees of freedom.
- 3. Set
- If
then 
has a noncentral chi-squared distribution with two degrees of freedom and noncentrality parameter 
. - If
then 
, and 
has an exponential distributionExponential distributionIn probability theory and statistics, the exponential distribution is a family of continuous probability distributions. It describes the time between events in a Poisson process, i.e...
.
Limiting cases
For large values of the argument, the Laguerre polynomial becomes (see Abramowitz and Stegun §13.5.1)It is seen that as ν becomes large or σ becomes small the mean becomes ν and the variance becomes σ2.
Parameter estimation (the Koay inversion technique)
There are three different methods for estimating the Rice parameters, (1) method of moments, (2) method of maximum likelihood, and (3) method of least squares. The first two methods have been investigated by Talukdar et al. and Bonny et al. and Sijbers et al.Here the interest is in estimating the parameters of the distribution, ν and σ, from a sample of data. This can be done using the method of moments, e.g., the sample mean and the sample standard deviation. The sample mean is an estimate of μ1' and the sample standard deviation is an estimate of μ21/2.
The following is an efficient method, known as the "Koay inversion technique", published by Koay et al. for solving the estimating equations
Estimating equations
In statistics, the method of estimating equations is a way of specifying how the parameters of a statistical model should be estimated. This can be thought of as a generalisation of many classical methods --- the method of moments, least squares, and maximum likelihood --- as well as some recent...
, based on the sample mean and the sample standard deviation, simultaneously . This inversion technique is also known as the fixed point
Fixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
formula of SNR. Earlier works on the method of moments usually use a root-finding method to solve the problem, which is not efficient.
First, the ratio of the sample mean to the sample standard deviation is defined as r, i.e.,
. The fixed point formula of SNR is expressed aswhere
is the ratio of the parameters, i.e., , and is given by:where
and are modified Bessel functions of the first kind.Note that
is a scaling factor of and is related to by:To find the fixed point,
, of , an initial solution is selected, , that is greater than the lower bound, which is and occurs when (Notice that this is the of a Rayleigh). This provides a starting point for the iteration, which uses functional composition, and this continues until is less than some small positive value. Here, denotes the composition of the same function, , -th times. In practice, we associate the final for some integer as the fixed point, , i.e., .Once the fixed point is found, the estimates
and are found through the scaling function, , as follows:,and
.To speed up the iteration even more, one can use the Newton's method of root-finding as presented by Koay et al. This particular approach is highly efficient.
The author has also provided an online calculator for computing the fixed point, which is also known as the underlying SNR from
, the magnitude SNR. See the link here under the subtitle called HI-SPEED SNR Analysis I. Note that the number of combined channel is 1 for the Rician distribution.External links
- MATLAB code for Rice/Rician distribution (PDF, mean and variance, and generating random samples)