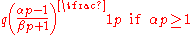Beta prime distribution
Encyclopedia
In probability theory
and statistics
, the beta prime distribution (also known as inverted beta distribution or beta distribution of the second kind) is an absolutely continuous probability distribution defined for with two parameters α and β, having the probability density function
with two parameters α and β, having the probability density function
:
where B is a Beta function. While the related beta distribution is the conjugate prior distribution of the parameter of a Bernoulli distribution expressed as a probability, the beta prime distribution is the conjugate prior distribution of the parameter of a Bernoulli distribution expressed in odds
. The distribution is a Pearson type VI distribution.
The mode of a variate X distributed as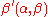 is
is 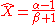 .
.
Its mean is if
if  (if
(if  the mean is infinite, in other words it has no well defined mean)
the mean is infinite, in other words it has no well defined mean)
and its variance is
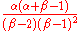 if
if  .
.
For , the k-th moment
, the k-th moment 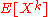 is given by
is given by
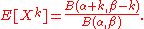
For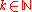 with
with  , this simplifies to
, this simplifies to
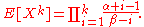
The cdf can also be written as

where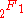 is the Gauss's hypergeometric function 2F1 .
is the Gauss's hypergeometric function 2F1 .
 shape
shape
(real
)
 scale (real
scale (real
)
having the probability density function
:
with mean
and mode
Note that if p=q=1 then the generalized beta prime distribution reduces to the standard beta prime distribution
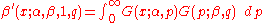
where G(x;a,b) is the gamma distribution with shape a and inverse scale b. This relationship can be used to generate random variables with a compound gamma, or beta prime distribution.
The mode, mean and variance of the compound gamma can be obtained by multiplying the mode and mean in the above infobox by q and the variance by q2.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
and statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the beta prime distribution (also known as inverted beta distribution or beta distribution of the second kind) is an absolutely continuous probability distribution defined for
 with two parameters α and β, having the probability density function
with two parameters α and β, having the probability density functionProbability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
:
where B is a Beta function. While the related beta distribution is the conjugate prior distribution of the parameter of a Bernoulli distribution expressed as a probability, the beta prime distribution is the conjugate prior distribution of the parameter of a Bernoulli distribution expressed in odds
Odds
The odds in favor of an event or a proposition are expressed as the ratio of a pair of integers, which is the ratio of the probability that an event will happen to the probability that it will not happen...
. The distribution is a Pearson type VI distribution.
The mode of a variate X distributed as
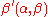 is
is 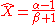 .
.Its mean is
 if
if  (if
(if  the mean is infinite, in other words it has no well defined mean)
the mean is infinite, in other words it has no well defined mean)and its variance is
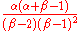 if
if  .
.For
 , the k-th moment
, the k-th moment 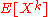 is given by
is given by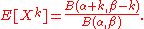
For
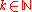 with
with  , this simplifies to
, this simplifies to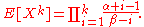
The cdf can also be written as

where
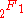 is the Gauss's hypergeometric function 2F1 .
is the Gauss's hypergeometric function 2F1 .Generalization
Two more parameters can be added to form the generalized beta prime distribution. shape
shapeShape parameter
In probability theory and statistics, a shape parameter is a kind of numerical parameter of a parametric family of probability distributions.- Definition :...
(real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
)
 scale (real
scale (realReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
)
having the probability density function
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
:
with mean
Mean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
and mode
Mode (statistics)
In statistics, the mode is the value that occurs most frequently in a data set or a probability distribution. In some fields, notably education, sample data are often called scores, and the sample mode is known as the modal score....
Note that if p=q=1 then the generalized beta prime distribution reduces to the standard beta prime distribution
Compound gamma distribution
The compound gamma distribution is the generalization of the beta prime when the scale parameter, q is added, but where p=1. It is so named because it is formed by compounding two gamma distributions: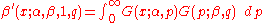
where G(x;a,b) is the gamma distribution with shape a and inverse scale b. This relationship can be used to generate random variables with a compound gamma, or beta prime distribution.
The mode, mean and variance of the compound gamma can be obtained by multiplying the mode and mean in the above infobox by q and the variance by q2.
Properties
- If
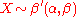 then
then 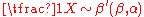 .
. - If
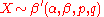 then
then 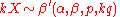 .
. 
Related distributions
- If
 then
then 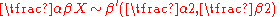
- If
 then
then 
- If
 and
and  , then
, then 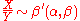 .
.  the Dagum distribution
the Dagum distribution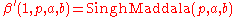 the Singh Maddala distribution
the Singh Maddala distribution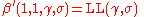 the Log logistic distribution
the Log logistic distribution- Beta prime distribution is a special case of the type 6 Pearson distributionPearson distributionThe Pearson distribution is a family of continuous probability distributions. It was first published by Karl Pearson in 1895 and subsequently extended by him in 1901 and 1916 in a series of articles on biostatistics.- History :...
- Pareto distribution type II is related to Beta prime distribution
- Pareto distribution type IV is related to Beta prime distribution