Rayleigh distribution
Encyclopedia
In probability theory
and statistics
, the Rayleigh distribution (icon) is a continuous probability distribution. A Rayleigh distribution is often observed when the overall magnitude of a vector is related to its directional components. One example where the Rayleigh distribution naturally arises is when wind speed is analyzed into its orthogonal 2-dimensional vector components. Assuming that the magnitude of each component is uncorrelated
and normally distributed with equal variance
, then the overall wind speed (vector magnitude) will be characterized by a Rayleigh distribution. A second example of the distribution arises in the case of random complex numbers whose real and imaginary components are i.i.d. (independently and identically distributed) Gaussian. In that case, the absolute value of the complex number is Rayleigh-distributed. The distribution is named after Lord Rayleigh
.
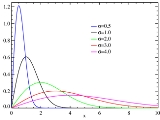
The Rayleigh probability density function
is
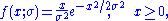
for parameter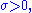
and cumulative distribution function
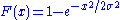
for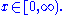
are given by:
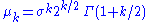
where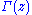
is the Gamma function
.
The mean
and variance
of a Rayleigh random variable
may be expressed as:
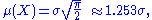
and
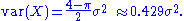
The mode is
and the maximum pdf is
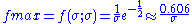
The skewness
is given by:
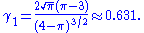
The excess kurtosis
is given by:
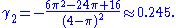
The characteristic function
is given by:
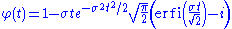
where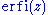
is the imaginary error function
. The moment generating function is given by
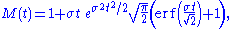
where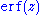
is the error function
.
1
+
\ln\left(\frac{\sigma}{\sqrt{2}}\right)
+
\frac{\gamma}{2}
where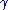
is the Euler–Mascheroni constant
.
, the maximum likelihood
estimate of
is
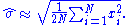
An application of the estimation of
can be found in magnetic resonance imaging (MRI). As MRI images are recorded as complex images but most often viewed as magnitude images, the background data is Rayleigh distributed. Hence, the above formula can be used to estimate the noise variance in an MRI image from background data.
in the interval(0, 1) , then the variate
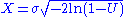
has a Rayleigh distribution with parameter
. This follows from the form of the cumulative distribution function. Given that U is uniform, (1–U) has the same uniformity and the above may be simplified to
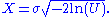
Note that if you are generating random numbers belonging to [0,1), exclude zero values to avoid the natural log of zero.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
and statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the Rayleigh distribution (icon) is a continuous probability distribution. A Rayleigh distribution is often observed when the overall magnitude of a vector is related to its directional components. One example where the Rayleigh distribution naturally arises is when wind speed is analyzed into its orthogonal 2-dimensional vector components. Assuming that the magnitude of each component is uncorrelated
Uncorrelated
In probability theory and statistics, two real-valued random variables are said to be uncorrelated if their covariance is zero. Uncorrelatedness is by definition pairwise; i.e...
and normally distributed with equal variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
, then the overall wind speed (vector magnitude) will be characterized by a Rayleigh distribution. A second example of the distribution arises in the case of random complex numbers whose real and imaginary components are i.i.d. (independently and identically distributed) Gaussian. In that case, the absolute value of the complex number is Rayleigh-distributed. The distribution is named after Lord Rayleigh
John Strutt, 3rd Baron Rayleigh
John William Strutt, 3rd Baron Rayleigh, OM was an English physicist who, with William Ramsay, discovered the element argon, an achievement for which he earned the Nobel Prize for Physics in 1904...
.
The Rayleigh probability density function
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
is
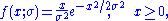
for parameter
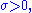and cumulative distribution functionCumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
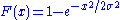
for
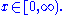
Properties
The raw momentsMoment (mathematics)
In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...
are given by:
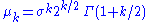
where
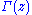is the Gamma functionGamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
.
The mean
Mean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
and variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
of a Rayleigh random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
may be expressed as:
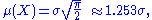
and
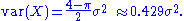
The mode is
and the maximum pdf is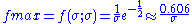The skewness
Skewness
In probability theory and statistics, skewness is a measure of the asymmetry of the probability distribution of a real-valued random variable. The skewness value can be positive or negative, or even undefined...
is given by:
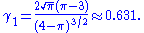
The excess kurtosis
Kurtosis
In probability theory and statistics, kurtosis is any measure of the "peakedness" of the probability distribution of a real-valued random variable...
is given by:
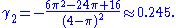
The characteristic function
Characteristic function (probability theory)
In probability theory and statistics, the characteristic function of any random variable completely defines its probability distribution. Thus it provides the basis of an alternative route to analytical results compared with working directly with probability density functions or cumulative...
is given by:
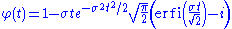
where
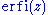is the imaginary error functionError function
In mathematics, the error function is a special function of sigmoid shape which occurs in probability, statistics and partial differential equations...
. The moment generating function is given by
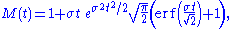
where
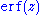is the error functionError function
In mathematics, the error function is a special function of sigmoid shape which occurs in probability, statistics and partial differential equations...
.
1
+
\ln\left(\frac{\sigma}{\sqrt{2}}\right)
+
\frac{\gamma}{2}
where
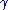is the Euler–Mascheroni constantEuler–Mascheroni constant
The Euler–Mascheroni constant is a mathematical constant recurring in analysis and number theory, usually denoted by the lowercase Greek letter ....
.
Parameter estimation
Given N independent and identically distributed Rayleigh random variables with parameter, the maximum likelihoodMaximum likelihood
In statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....
estimate of
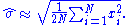
isAn application of the estimation of
can be found in magnetic resonance imaging (MRI). As MRI images are recorded as complex images but most often viewed as magnitude images, the background data is Rayleigh distributed. Hence, the above formula can be used to estimate the noise variance in an MRI image from background data.Generating Rayleigh-distributed random variates
Given a random variate U drawn from the uniform distributionUniform distribution (continuous)
In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of probability distributions such that for each member of the family, all intervals of the same length on the distribution's support are equally probable. The support is defined by...
in the interval
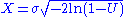
has a Rayleigh distribution with parameter
. This follows from the form of the cumulative distribution function. Given that U is uniform, (1–U) has the same uniformity and the above may be simplified to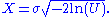Note that if you are generating random numbers belonging to [0,1), exclude zero values to avoid the natural log of zero.
Related distributions
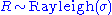is Rayleigh distributed if 
, where 
and 
are independent normal random variables. (This gives motivation to the use of the symbol "sigma" in the above parameterization of the Rayleigh density.)- If
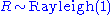, then 
has a chi-squared distribution with two degrees of freedom: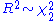 
- If
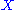has an exponential distributionExponential distributionIn probability theory and statistics, the exponential distribution is a family of continuous probability distributions. It describes the time between events in a Poisson process, i.e...
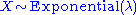, then 
.
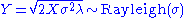- If
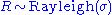, then 
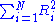has a gamma distribution with parameters 
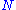and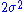 
: 
.
- The Chi distribution is a generalization of the Rayleigh distribution.
- The Rice distributionRice distributionIn probability theory, the Rice distribution or Rician distribution is the probability distribution of the absolute value of a circular bivariate normal random variable with potentially non-zero mean. It was named after Stephen O...
is a generalization of the Rayleigh distribution. - The Weibull distribution is a generalization of the Rayleigh distribution. In this instance, parameter
is related to the Weibull scale parameter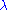 
: 
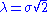. - The Maxwell–Boltzmann distribution describes the magnitude of a normal vector in three dimensions.
See also
- Rayleigh fadingRayleigh fadingRayleigh fading is a statistical model for the effect of a propagation environment on a radio signal, such as that used by wireless devices.Rayleigh fading models assume that the magnitude of a signal that has passed through such a transmission medium will vary randomly, or fade, according to a...
- Rice distributionRice distributionIn probability theory, the Rice distribution or Rician distribution is the probability distribution of the absolute value of a circular bivariate normal random variable with potentially non-zero mean. It was named after Stephen O...