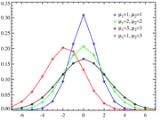
Skellam distribution
Encyclopedia
The Skellam distribution is the discrete probability distribution
of the difference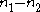 of two statistically independent random variable
of two statistically independent random variable
s and
and 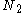 each having Poisson distribution
each having Poisson distribution
s with different expected value
s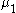 and
and 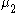 . It is useful in describing the statistics of the difference of two images with simple photon noise, as well as describing the point spread
. It is useful in describing the statistics of the difference of two images with simple photon noise, as well as describing the point spread
distribution in certain sports where all scored points are equal, such as baseball
, hockey
and soccer.
The distribution is also applicable to a special case of the difference of dependent Poisson random variables, but just the obvious case where the two variables have a common additive random contribution which is cancelled by the differencing: see Karlis & Ntzoufras (2003) for details and an application.
The probability mass function
for the Skellam distribution for a count difference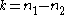 from two Poisson-distributed variables with means
from two Poisson-distributed variables with means 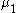 and
and 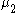 is given by:
is given by:
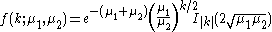
where Ik(z) is the modified Bessel function
of the first kind.
of a Poisson distribution
for a count n with mean μ is given by
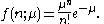
for (and zero otherwise). The Skellam probability mass function for the difference of two counts
(and zero otherwise). The Skellam probability mass function for the difference of two counts 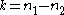 is the cross-correlation
is the cross-correlation
of two Poisson distributions: (Skellam
, 1946)
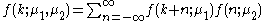
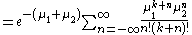
Since the Poisson distribution is zero for negative values of the count, all terms with negative factorials in the above sum are set to zero. It can be shown that the above sum implies that

so that:
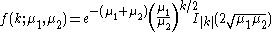
where I k(z) is the modified Bessel function
of the first kind. The special case for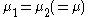 is given by Irwin (1937):
is given by Irwin (1937):
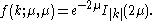
Note also that, using the limiting values of the modified Bessel function for small arguments, we can recover the Poisson distribution as a special case of the Skellam distribution for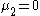 .
.
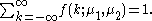
We know that the probability generating function
(pgf) for a
Poisson distribution
is:
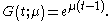
It follows that the pgf,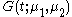 , for a Skellam probability function will be:
, for a Skellam probability function will be:
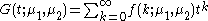
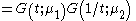
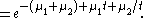
Notice that the form of the
probability generating function
implies that the
distribution of the sums or the differences of any number of independent
Skellam-distributed variables are again Skellam-distributed. It is sometimes claimed that any linear combination of two Skellam-distributed
variables are again Skellam-distributed, but this is clearly not true since
any multiplier other than +/-1 would change the support
of the distribution.
The moment-generating function
is given by:
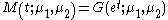

which yields the raw moments mk . Define:


Then the raw moments mk are

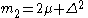
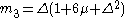
The central moments M k are
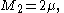
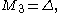
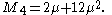
The mean
, variance
,
skewness
, and kurtosis excess
are respectively:
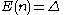
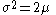
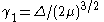
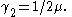
The cumulant-generating function is given by:
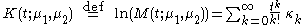
which yields the cumulant
s:
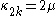
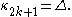
For the special case when μ1 = μ2, an
asymptotic expansion
of the modified Bessel function of the first kind
yields for large μ:
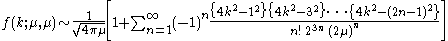
(Abramowitz & Stegun 1972, p. 377).
Also, for this special case, when k is also large, and of
order
of the square root of 2μ, the distribution
tends to a normal distribution:
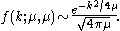
These special results can easily be extended to the more general case of
different means.
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
of the difference
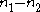 of two statistically independent random variable
of two statistically independent random variableRandom variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s
 and
and 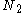 each having Poisson distribution
each having Poisson distributionPoisson distribution
In probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time and/or space if these events occur with a known average rate and independently of the time since...
s with different expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
s
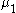 and
and 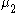 . It is useful in describing the statistics of the difference of two images with simple photon noise, as well as describing the point spread
. It is useful in describing the statistics of the difference of two images with simple photon noise, as well as describing the point spreadSpread betting
Spread betting is any of various types of wagering on the outcome of an event, where the pay-off is based on the accuracy of the wager, rather than a simple "win or lose" outcome, such as fixed-odds betting or parimutuel betting. A spread is a range of outcomes and the bet is whether the outcome...
distribution in certain sports where all scored points are equal, such as baseball
Baseball
Baseball is a bat-and-ball sport played between two teams of nine players each. The aim is to score runs by hitting a thrown ball with a bat and touching a series of four bases arranged at the corners of a ninety-foot diamond...
, hockey
Ice hockey
Ice hockey, often referred to as hockey, is a team sport played on ice, in which skaters use wooden or composite sticks to shoot a hard rubber puck into their opponent's net. The game is played between two teams of six players each. Five members of each team skate up and down the ice trying to take...
and soccer.
The distribution is also applicable to a special case of the difference of dependent Poisson random variables, but just the obvious case where the two variables have a common additive random contribution which is cancelled by the differencing: see Karlis & Ntzoufras (2003) for details and an application.
The probability mass function
Probability mass function
In probability theory and statistics, a probability mass function is a function that gives the probability that a discrete random variable is exactly equal to some value...
for the Skellam distribution for a count difference
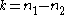 from two Poisson-distributed variables with means
from two Poisson-distributed variables with means 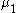 and
and 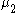 is given by:
is given by: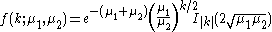
where Ik(z) is the modified Bessel function
Bessel function
In mathematics, Bessel functions, first defined by the mathematician Daniel Bernoulli and generalized by Friedrich Bessel, are canonical solutions y of Bessel's differential equation:...
of the first kind.
Derivation
Note that the probability mass functionProbability mass function
In probability theory and statistics, a probability mass function is a function that gives the probability that a discrete random variable is exactly equal to some value...
of a Poisson distribution
Poisson distribution
In probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time and/or space if these events occur with a known average rate and independently of the time since...
for a count n with mean μ is given by
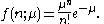
for
 (and zero otherwise). The Skellam probability mass function for the difference of two counts
(and zero otherwise). The Skellam probability mass function for the difference of two counts 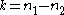 is the cross-correlation
is the cross-correlationCross-correlation
In signal processing, cross-correlation is a measure of similarity of two waveforms as a function of a time-lag applied to one of them. This is also known as a sliding dot product or sliding inner-product. It is commonly used for searching a long-duration signal for a shorter, known feature...
of two Poisson distributions: (Skellam
John Gordon Skellam
John Gordon Skellam was born in Staffordshire county in 1914, died during the summer of 1979. He was educated at Hanley High School where he won several scholarships including free admission to New College in Oxford...
, 1946)
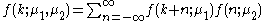
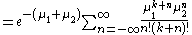
Since the Poisson distribution is zero for negative values of the count, all terms with negative factorials in the above sum are set to zero. It can be shown that the above sum implies that

so that:
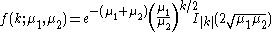
where I k(z) is the modified Bessel function
Bessel function
In mathematics, Bessel functions, first defined by the mathematician Daniel Bernoulli and generalized by Friedrich Bessel, are canonical solutions y of Bessel's differential equation:...
of the first kind. The special case for
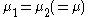 is given by Irwin (1937):
is given by Irwin (1937):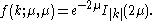
Note also that, using the limiting values of the modified Bessel function for small arguments, we can recover the Poisson distribution as a special case of the Skellam distribution for
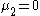 .
.Properties
As it is a discrete probability function, the Skellam probability mass function is normalized: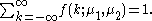
We know that the probability generating function
Probability-generating function
In probability theory, the probability-generating function of a discrete random variable is a power series representation of the probability mass function of the random variable...
(pgf) for a
Poisson distribution
Poisson distribution
In probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time and/or space if these events occur with a known average rate and independently of the time since...
is:
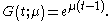
It follows that the pgf,
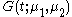 , for a Skellam probability function will be:
, for a Skellam probability function will be: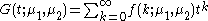
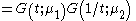
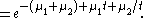
Notice that the form of the
probability generating function
Probability-generating function
In probability theory, the probability-generating function of a discrete random variable is a power series representation of the probability mass function of the random variable...
implies that the
distribution of the sums or the differences of any number of independent
Skellam-distributed variables are again Skellam-distributed. It is sometimes claimed that any linear combination of two Skellam-distributed
variables are again Skellam-distributed, but this is clearly not true since
any multiplier other than +/-1 would change the support
Support (mathematics)
In mathematics, the support of a function is the set of points where the function is not zero, or the closure of that set . This concept is used very widely in mathematical analysis...
of the distribution.
The moment-generating function
Moment-generating function
In probability theory and statistics, the moment-generating function of any random variable is an alternative definition of its probability distribution. Thus, it provides the basis of an alternative route to analytical results compared with working directly with probability density functions or...
is given by:
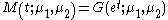

which yields the raw moments mk . Define:


Then the raw moments mk are

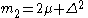
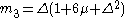
The central moments M k are
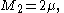
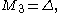
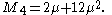
The mean
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
, variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
,
skewness
Skewness
In probability theory and statistics, skewness is a measure of the asymmetry of the probability distribution of a real-valued random variable. The skewness value can be positive or negative, or even undefined...
, and kurtosis excess
Kurtosis
In probability theory and statistics, kurtosis is any measure of the "peakedness" of the probability distribution of a real-valued random variable...
are respectively:
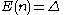
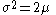
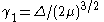
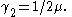
The cumulant-generating function is given by:
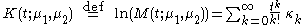
which yields the cumulant
Cumulant
In probability theory and statistics, the cumulants κn of a probability distribution are a set of quantities that provide an alternative to the moments of the distribution. The moments determine the cumulants in the sense that any two probability distributions whose moments are identical will have...
s:
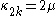
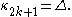
For the special case when μ1 = μ2, an
asymptotic expansion
Asymptotic expansion
In mathematics an asymptotic expansion, asymptotic series or Poincaré expansion is a formal series of functions which has the property that truncating the series after a finite number of terms provides an approximation to a given function as the argument of the function tends towards a particular,...
of the modified Bessel function of the first kind
Bessel function
In mathematics, Bessel functions, first defined by the mathematician Daniel Bernoulli and generalized by Friedrich Bessel, are canonical solutions y of Bessel's differential equation:...
yields for large μ:
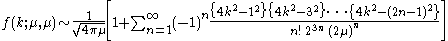
(Abramowitz & Stegun 1972, p. 377).
Also, for this special case, when k is also large, and of
order
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
of the square root of 2μ, the distribution
tends to a normal distribution:
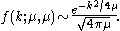
These special results can easily be extended to the more general case of
different means.

