Standard distribution

In probability theory

Probability theory

Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...

, the arcsine distribution is the probability distribution

Probability distribution

In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....

 whose cumulative distribution function

Cumulative distribution function

In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...

 is


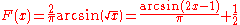
for 0 ≤ x ≤ 1, and whose probability density function is


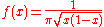
on (0, 1). The standard arcsine distribution is a special case of the beta distribution with α = β = 1/2. That is, if is the standard arcsine distribution then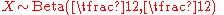

The arcsine distribution appears

• in the Lévy arcsine law
  Lévy arcsine law
  In probability theory, the Lévy arcsine law, found by , states that the probability distribution of the proportion of the time that a Wiener process is positive is a random variable whose probability distribution is the arcsine distribution...
  
  ;
• in the Erdős arcsine law
  Erdős arcsine law
  In number theory, the Erdős arcsine law, named after Paul Erdős, states that the prime divisors of a number have a distribution related to the arcsine distribution....
  
  ;
• as the Jeffreys prior
  Jeffreys prior
  In Bayesian probability, the Jeffreys prior, named after Harold Jeffreys, is a non-informative prior distribution on parameter space that is proportional to the square root of the determinant of the Fisher information:...
  
   for the probability of success of a Bernoulli trial
  Bernoulli trial
  In the theory of probability and statistics, a Bernoulli trial is an experiment whose outcome is random and can be either of two possible outcomes, "success" and "failure"....
  
  .

Generalization

Arbitrary bounded support

The distribution can be expanded to include any bounded support from a ≤ x ≤ b by a simple transformation


for a ≤ x ≤ b, and whose probability density function

Probability density function

In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...

 is


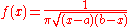
on (a, b).

Shape factor

The generalized standard arcsine distribution on (0,1) with probability density function


is also a special case of the beta distribution with parameters .

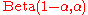Note that when 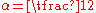the general arcsine distribution reduces to the standard distribution listed above.

Properties

• Arcsine distribution is closed under translation and scaling by a positive factor
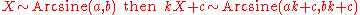
  • If
• The square of an arc sine distribution over (-1, 1) has arc sine distribution over (0, 1)
  • If

Related distributions

• If U and V are i.i.d
  Independent and identically distributed random variables
  In probability theory and statistics, a sequence or other collection of random variables is independent and identically distributed if each random variable has the same probability distribution as the others and all are mutually independent....
  
    uniform
  Uniform distribution (continuous)
  In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of probability distributions such that for each member of the family, all intervals of the same length on the distribution's support are equally probable. The support is defined by...
  
  (−π,π) random variables, then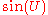 , , 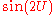, 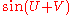and 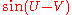all have a standard arcsine distribution
• If is the generalized arcsine distribution with shape parameter supported on the finite interval [a,b] then