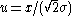
Voigt profile
Encyclopedia
In spectroscopy
, the Voigt profile (named after Woldemar Voigt
) is a line profile
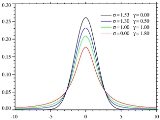
resulting from the convolution of two broadening mechanisms, one of which alone would produce a Gaussian profile (usually, as a result of the Doppler broadening
), and the other would produce a Lorentzian profile. Voigt profiles are common in many branches of spectroscopy and diffraction
. Due to the computational expense of the convolution operation, the Voigt profile is often approximated using a pseudo-Voigt profile.
All normalized line profiles can be considered to be probability distribution
s. The Gaussian profile is equivalent to a Gaussian or normal distribution and a Lorentzian profile is equivalent to a Lorentz or Cauchy distribution
. Without loss of generality, we can consider only centered profiles which peak at zero. The Voigt profile is then a convolution
of a Lorentz profile and a Gaussian profile:
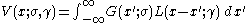
where x is frequency from line center,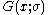 is the centered Gaussian profile:
is the centered Gaussian profile:
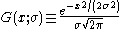
and is the centered Lorentzian profile:
is the centered Lorentzian profile:
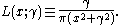
The defining integral can be evaluated as:
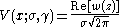
where Re[w(z) ] is the real
part of the complex error function
of z and
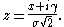
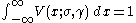
since it is the convolution of normalized profiles. The Lorentzian profile has no moments (other than the zeroth) and so the moment-generating function
for the Cauchy distribution
is not defined. It follows that the Voigt profile will not have a moment-generating function either, but the characteristic function
for the Cauchy distribution
is well defined, as is the characteristic function for the normal distribution. The characteristic function
for the (centered) Voigt profile will then be the product of the two:
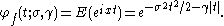
Since both the normal and the Cauchy distribution are stable distributions, they are closed under convolution
and it follows that the Voigt distribution will also be closed under convolution.

Substituting the definition of the complex error function
yields for the indefinite integral:
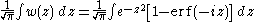
Which may be solved to yield:
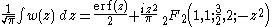
where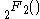 is a hypergeometric function. In order for the function to approach zero as x approaches negative infinity (as the CDF must do), an integration constant of 1/2 must be added. This gives for the CDF:
is a hypergeometric function. In order for the function to approach zero as x approaches negative infinity (as the CDF must do), an integration constant of 1/2 must be added. This gives for the CDF:

(FWHM) of the Voigt profile can be found from the
widths of the associated Gaussian and Lorentzian widths. The FWHM of the Gaussian profile
is
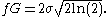
The FWHM of the Lorentzian profile is just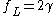 . Define
. Define
φ =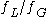 . Then the FWHM of the Voigt profile (
. Then the FWHM of the Voigt profile (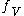 ) can be estimated as:
) can be estimated as:
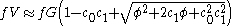
where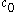 = 2.0056 and
= 2.0056 and 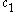 = 1.0593. This estimate will have a standard deviation of error of about 2.4 percent for values of φ between 0 and 10. Note that the above equation will be exactly correct in the limit of φ = 0 and φ = ∞, that is for pure Gaussian and Lorentzian profiles.
= 1.0593. This estimate will have a standard deviation of error of about 2.4 percent for values of φ between 0 and 10. Note that the above equation will be exactly correct in the limit of φ = 0 and φ = ∞, that is for pure Gaussian and Lorentzian profiles.
A better approximation with an accuracy of 0.02% is given by
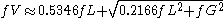 .
.
Note that this approximation will be exactly correct for a pure Gaussian, but will have an error of about 0.0325 percent for a pure Lorentzian profile.
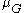 and the Lorentzian profile is centered at
and the Lorentzian profile is centered at 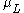 , the convolution will be centered at
, the convolution will be centered at 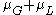 and the characteristic function will then be:
and the characteristic function will then be:
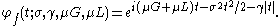
The mode and median will then both be located at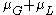 .
.


where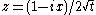
and erfc is the complementary error function.
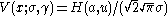 ,
,
with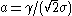
and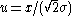
Spectroscopy
Spectroscopy is the study of the interaction between matter and radiated energy. Historically, spectroscopy originated through the study of visible light dispersed according to its wavelength, e.g., by a prism. Later the concept was expanded greatly to comprise any interaction with radiative...
, the Voigt profile (named after Woldemar Voigt
Woldemar Voigt
Woldemar Voigt was a German physicist, who taught at the Georg August University of Göttingen. Voigt eventually went on to head the Mathematical Physics Department at Göttingen and was succeeded in 1914 by Peter Debye, who took charge of the theoretical department of the Physical Institute...
) is a line profile
Spectral line
A spectral line is a dark or bright line in an otherwise uniform and continuous spectrum, resulting from a deficiency or excess of photons in a narrow frequency range, compared with the nearby frequencies.- Types of line spectra :...
resulting from the convolution of two broadening mechanisms, one of which alone would produce a Gaussian profile (usually, as a result of the Doppler broadening
Doppler broadening
In atomic physics, Doppler broadening is the broadening of spectral lines due to the Doppler effect caused by a distribution of velocities of atoms or molecules. Different velocities of the emitting particles result in different shifts, the cumulative effect of which is the line broadening.The...
), and the other would produce a Lorentzian profile. Voigt profiles are common in many branches of spectroscopy and diffraction
Powder diffraction
Powder diffraction is a scientific technique using X-ray, neutron, or electron diffraction on powder or microcrystalline samples for structural characterization of materials.-Explanation:...
. Due to the computational expense of the convolution operation, the Voigt profile is often approximated using a pseudo-Voigt profile.
All normalized line profiles can be considered to be probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
s. The Gaussian profile is equivalent to a Gaussian or normal distribution and a Lorentzian profile is equivalent to a Lorentz or Cauchy distribution
Cauchy distribution
The Cauchy–Lorentz distribution, named after Augustin Cauchy and Hendrik Lorentz, is a continuous probability distribution. As a probability distribution, it is known as the Cauchy distribution, while among physicists, it is known as the Lorentz distribution, Lorentz function, or Breit–Wigner...
. Without loss of generality, we can consider only centered profiles which peak at zero. The Voigt profile is then a convolution
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
of a Lorentz profile and a Gaussian profile:
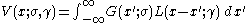
where x is frequency from line center,
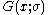 is the centered Gaussian profile:
is the centered Gaussian profile: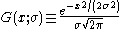
and
 is the centered Lorentzian profile:
is the centered Lorentzian profile: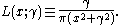
The defining integral can be evaluated as:
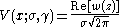
where Re[w(z) ] is the real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
part of the complex error function
Error function
In mathematics, the error function is a special function of sigmoid shape which occurs in probability, statistics and partial differential equations...
of z and
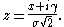
Properties
The Voigt profile is normalized: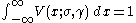
since it is the convolution of normalized profiles. The Lorentzian profile has no moments (other than the zeroth) and so the moment-generating function
Moment-generating function
In probability theory and statistics, the moment-generating function of any random variable is an alternative definition of its probability distribution. Thus, it provides the basis of an alternative route to analytical results compared with working directly with probability density functions or...
for the Cauchy distribution
Cauchy distribution
The Cauchy–Lorentz distribution, named after Augustin Cauchy and Hendrik Lorentz, is a continuous probability distribution. As a probability distribution, it is known as the Cauchy distribution, while among physicists, it is known as the Lorentz distribution, Lorentz function, or Breit–Wigner...
is not defined. It follows that the Voigt profile will not have a moment-generating function either, but the characteristic function
Characteristic function (probability theory)
In probability theory and statistics, the characteristic function of any random variable completely defines its probability distribution. Thus it provides the basis of an alternative route to analytical results compared with working directly with probability density functions or cumulative...
for the Cauchy distribution
Cauchy distribution
The Cauchy–Lorentz distribution, named after Augustin Cauchy and Hendrik Lorentz, is a continuous probability distribution. As a probability distribution, it is known as the Cauchy distribution, while among physicists, it is known as the Lorentz distribution, Lorentz function, or Breit–Wigner...
is well defined, as is the characteristic function for the normal distribution. The characteristic function
Characteristic function (probability theory)
In probability theory and statistics, the characteristic function of any random variable completely defines its probability distribution. Thus it provides the basis of an alternative route to analytical results compared with working directly with probability density functions or cumulative...
for the (centered) Voigt profile will then be the product of the two:
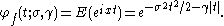
Since both the normal and the Cauchy distribution are stable distributions, they are closed under convolution
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
and it follows that the Voigt distribution will also be closed under convolution.
Cumulative distribution function
Using the above definition for z , the CDF can be found as follows:
Substituting the definition of the complex error function
Error function
In mathematics, the error function is a special function of sigmoid shape which occurs in probability, statistics and partial differential equations...
yields for the indefinite integral:
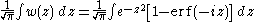
Which may be solved to yield:
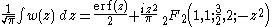
where
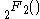 is a hypergeometric function. In order for the function to approach zero as x approaches negative infinity (as the CDF must do), an integration constant of 1/2 must be added. This gives for the CDF:
is a hypergeometric function. In order for the function to approach zero as x approaches negative infinity (as the CDF must do), an integration constant of 1/2 must be added. This gives for the CDF:
The width of the Voigt profile
The full width at half maximumFull width at half maximum
Full width at half maximum is an expression of the extent of a function, given by the difference between the two extreme values of the independent variable at which the dependent variable is equal to half of its maximum value....
(FWHM) of the Voigt profile can be found from the
widths of the associated Gaussian and Lorentzian widths. The FWHM of the Gaussian profile
is
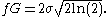
The FWHM of the Lorentzian profile is just
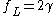 . Define
. Defineφ =
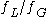 . Then the FWHM of the Voigt profile (
. Then the FWHM of the Voigt profile (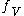 ) can be estimated as:
) can be estimated as: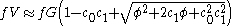
where
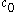 = 2.0056 and
= 2.0056 and 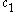 = 1.0593. This estimate will have a standard deviation of error of about 2.4 percent for values of φ between 0 and 10. Note that the above equation will be exactly correct in the limit of φ = 0 and φ = ∞, that is for pure Gaussian and Lorentzian profiles.
= 1.0593. This estimate will have a standard deviation of error of about 2.4 percent for values of φ between 0 and 10. Note that the above equation will be exactly correct in the limit of φ = 0 and φ = ∞, that is for pure Gaussian and Lorentzian profiles.A better approximation with an accuracy of 0.02% is given by
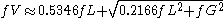 .
.Note that this approximation will be exactly correct for a pure Gaussian, but will have an error of about 0.0325 percent for a pure Lorentzian profile.
The uncentered Voigt profile
If the Gaussian profile is centered at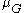 and the Lorentzian profile is centered at
and the Lorentzian profile is centered at 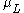 , the convolution will be centered at
, the convolution will be centered at 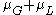 and the characteristic function will then be:
and the characteristic function will then be: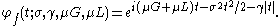
The mode and median will then both be located at
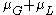 .
.Voigt functions
The Voigt functions U, V, and H (sometimes called the line broadening function) are defined by

where
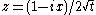
and erfc is the complementary error function.
Relation to Voigt Profile
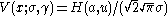 ,
,with
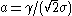
and