
Type-2 Gumbel distribution
Encyclopedia
In probability theory
, the Type-2 Gumbel probability density function
is
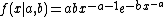
for
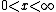 .
.
This implies that it is similar to the Weibull distributions, substituting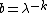 and
and  . Note however that a positive k (as in the Weibull distribution) would yield a negative a, which is not allowed here as it would yield a negative probability density.
. Note however that a positive k (as in the Weibull distribution) would yield a negative a, which is not allowed here as it would yield a negative probability density.
For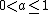 the mean
the mean
is infinite. For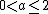 the variance
the variance
is infinite.
The cumulative distribution function
is
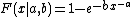
The moments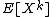 exist for
exist for 
The special case b = 1 yields the Fréchet distribution
----
Based on The GNU Scientific Library, used under GFDL.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, the Type-2 Gumbel probability density function
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
is
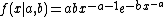
for
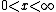 .
.This implies that it is similar to the Weibull distributions, substituting
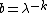 and
and  . Note however that a positive k (as in the Weibull distribution) would yield a negative a, which is not allowed here as it would yield a negative probability density.
. Note however that a positive k (as in the Weibull distribution) would yield a negative a, which is not allowed here as it would yield a negative probability density.For
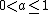 the mean
the meanMean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
is infinite. For
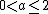 the variance
the varianceVariance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
is infinite.
The cumulative distribution function
Cumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
is
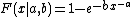
The moments
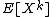 exist for
exist for 
The special case b = 1 yields the Fréchet distribution
----
Based on The GNU Scientific Library, used under GFDL.
See also
- Extreme value theoryExtreme value theoryExtreme value theory is a branch of statistics dealing with the extreme deviations from the median of probability distributions. The general theory sets out to assess the type of probability distributions generated by processes...
- Gumbel distribution
- Type-1 Gumbel distribution

