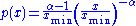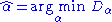Power law
Encyclopedia

Earthquake
An earthquake is the result of a sudden release of energy in the Earth's crust that creates seismic waves. The seismicity, seismism or seismic activity of an area refers to the frequency, type and size of earthquakes experienced over a period of time...
s, craters on the moon
Moon
The Moon is Earth's only known natural satellite,There are a number of near-Earth asteroids including 3753 Cruithne that are co-orbital with Earth: their orbits bring them close to Earth for periods of time but then alter in the long term . These are quasi-satellites and not true moons. For more...
and of solar flare
Solar flare
A solar flare is a sudden brightening observed over the Sun surface or the solar limb, which is interpreted as a large energy release of up to 6 × 1025 joules of energy . The flare ejects clouds of electrons, ions, and atoms through the corona into space. These clouds typically reach Earth a day...
s, the foraging pattern of various species, the sizes of activity patterns of neuronal populations, the frequencies of word
Word
In language, a word is the smallest free form that may be uttered in isolation with semantic or pragmatic content . This contrasts with a morpheme, which is the smallest unit of meaning but will not necessarily stand on its own...
s in most languages, frequencies of family name
Family name
A family name is a type of surname and part of a person's name indicating the family to which the person belongs. The use of family names is widespread in cultures around the world...
s, the sizes of power outage
Power outage
A power outage is a short- or long-term loss of the electric power to an area.There are many causes of power failures in an electricity network...
s and wars, and many other quantities. It also underlies the "80/20 rule" or Pareto distribution governing the distribution of income or wealth within a population.
Scale invariance
The main property of power laws that makes them interesting is their scale invariance. Given a relation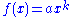 , scaling the argument
, scaling the argument  by a constant factor causes only a proportionate scaling of the function itself. That is,
by a constant factor causes only a proportionate scaling of the function itself. That is,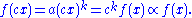
That is, scaling by a constant simply multiplies the original power-law relation by the constant
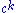 . Thus, it follows that all power laws with a particular scaling exponent are equivalent up to constant factors, since each is simply a scaled version of the others. This behavior is what produces the linear relationship when logarithms are taken of both
. Thus, it follows that all power laws with a particular scaling exponent are equivalent up to constant factors, since each is simply a scaled version of the others. This behavior is what produces the linear relationship when logarithms are taken of both 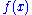 and
and  , and the straight-line on the log-log plot is often called the signature of a power law. With real data, such straightness is necessary, but not a sufficient condition for the data following a power-law relation. In fact, there are many ways to generate finite amounts of data that mimic this signature behavior, but, in their asymptotic limit, are not true power laws. Thus, accurately fitting and validating power-law models is an active area of research in statistics
, and the straight-line on the log-log plot is often called the signature of a power law. With real data, such straightness is necessary, but not a sufficient condition for the data following a power-law relation. In fact, there are many ways to generate finite amounts of data that mimic this signature behavior, but, in their asymptotic limit, are not true power laws. Thus, accurately fitting and validating power-law models is an active area of research in statisticsStatistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
.
Universality
The equivalence of power laws with a particular scaling exponent can have a deeper origin in the dynamical processes that generate the power-law relation. In physics, for example, phase transitionPhase transition
A phase transition is the transformation of a thermodynamic system from one phase or state of matter to another.A phase of a thermodynamic system and the states of matter have uniform physical properties....
s in thermodynamic systems are associated with the emergence of power-law distributions of certain quantities, whose exponents are referred to as the critical exponent
Critical exponent
Critical exponents describe the behaviour of physical quantities near continuous phase transitions. It is believed, though not proven, that they are universal, i.e...
s of the system. Diverse systems with the same critical exponents—that is, which display identical scaling behaviour as they approach criticality
Critical point (thermodynamics)
In physical chemistry, thermodynamics, chemistry and condensed matter physics, a critical point, also called a critical state, specifies the conditions at which a phase boundary ceases to exist...
—can be shown, via renormalization group
Renormalization group
In theoretical physics, the renormalization group refers to a mathematical apparatus that allows systematic investigation of the changes of a physical system as viewed at different distance scales...
theory, to share the same fundamental dynamics. For instance, the behavior of water and CO2 at their boiling points fall in the same universality class because they have identical critical exponents. In fact, almost all material phase transitions are described by a small set of universality classes. Similar observations have been made, though not as comprehensively, for various self-organized critical
Self-organized criticality
In physics, self-organized criticality is a property of dynamical systems which have a critical point as an attractor. Their macroscopic behaviour thus displays the spatial and/or temporal scale-invariance characteristic of the critical point of a phase transition, but without the need to tune...
systems, where the critical point of the system is an attractor
Attractor
An attractor is a set towards which a dynamical system evolves over time. That is, points that get close enough to the attractor remain close even if slightly disturbed...
. Formally, this sharing of dynamics is referred to as universality
Universality (dynamical systems)
In statistical mechanics, universality is the observation that there are properties for a large class of systems that are independent of the dynamical details of the system. Systems display universality in a scaling limit, when a large number of interacting parts come together...
, and systems with precisely the same critical exponents are said to belong to the same universality class.
Power-law functions
The general power-law function follows the polynomial form given above, and is a ubiquitous form throughout mathematics and science. Notably, however, not all polynomial functions are power laws because not all polynomials exhibit the property of scale invariance. Typically, power-law functions are polynomials in a single variable, and are explicitly used to model the scaling behavior of natural processes. For instance, allometric scaling laws for the relation of biological variables are some of the best known power-law functions in nature. In this context, the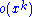 term is most typically replaced by a deviation term
term is most typically replaced by a deviation term  , which can represent uncertainty in the observed values (perhaps measurement or sampling errors) or provide a simple way for observations to deviate from the power-law function (perhaps for stochastic
, which can represent uncertainty in the observed values (perhaps measurement or sampling errors) or provide a simple way for observations to deviate from the power-law function (perhaps for stochasticStochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
reasons):
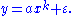
Scientific interest in power law relations stems partly from the ease with which certain general classes of mechanisms generate them (see the Sornette reference below). The demonstration of a power-law relation in some data can point to specific kinds of mechanisms that might underlie the natural phenomenon in question, and can indicate a deep connection with other, seemingly unrelated systems (see the reference by Simon and the subsection on universality below). The ubiquity of power-law relations in physics is partly due to dimensional constraints
Dimensional analysis
In physics and all science, dimensional analysis is a tool to find or check relations among physical quantities by using their dimensions. The dimension of a physical quantity is the combination of the basic physical dimensions which describe it; for example, speed has the dimension length per...
, while in complex systems
Complex systems
Complex systems present problems in mathematical modelling.The equations from which complex system models are developed generally derive from statistical physics, information theory and non-linear dynamics, and represent organized but unpredictable behaviors of systems of nature that are considered...
, power laws are often thought to be signatures of hierarchy or of specific stochastic processes. A few notable examples of power laws are the Gutenberg-Richter law
Gutenberg-Richter law
In seismology, the Gutenberg–Richter law expresses the relationship between the magnitude and total number of earthquakes in any given region and time period of at least that magnitude.orWhere:...
for earthquake sizes, Pareto's law
Pareto principle
The Pareto principle states that, for many events, roughly 80% of the effects come from 20% of the causes.Business-management consultant Joseph M...
of income distribution, structural self-similarity of fractals, and scaling laws in biological systems. Research on the origins of power-law relations, and efforts to observe and validate them in the real world, is an active topic of research in many fields of science, including physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, linguistics
Linguistics
Linguistics is the scientific study of human language. Linguistics can be broadly broken into three categories or subfields of study: language form, language meaning, and language in context....
, geophysics
Geophysics
Geophysics is the physics of the Earth and its environment in space; also the study of the Earth using quantitative physical methods. The term geophysics sometimes refers only to the geological applications: Earth's shape; its gravitational and magnetic fields; its internal structure and...
, neuroscience
Neuroscience
Neuroscience is the scientific study of the nervous system. Traditionally, neuroscience has been seen as a branch of biology. However, it is currently an interdisciplinary science that collaborates with other fields such as chemistry, computer science, engineering, linguistics, mathematics,...
, sociology
Sociology
Sociology is the study of society. It is a social science—a term with which it is sometimes synonymous—which uses various methods of empirical investigation and critical analysis to develop a body of knowledge about human social activity...
, economics
Economics
Economics is the social science that analyzes the production, distribution, and consumption of goods and services. The term economics comes from the Ancient Greek from + , hence "rules of the house"...
and more.
However much of the recent interest in power laws comes from the study of probability distributions: it's now known that the distributions of a wide variety of quantities seem to follow the power-law form, at least in their upper tail (large events). The behavior of these large events connects these quantities to the study of theory of large deviations
Extreme value theory
Extreme value theory is a branch of statistics dealing with the extreme deviations from the median of probability distributions. The general theory sets out to assess the type of probability distributions generated by processes...
(also called extreme value theory
Extreme value theory
Extreme value theory is a branch of statistics dealing with the extreme deviations from the median of probability distributions. The general theory sets out to assess the type of probability distributions generated by processes...
), which considers the frequency of extremely rare events like stock market crash
Stock market crash
A stock market crash is a sudden dramatic decline of stock prices across a significant cross-section of a stock market, resulting in a significant loss of paper wealth. Crashes are driven by panic as much as by underlying economic factors...
es and large natural disaster
Natural disaster
A natural disaster is the effect of a natural hazard . It leads to financial, environmental or human losses...
s. It is primarily in the study of statistical distributions that the name "power law" is used; in other areas the power-law functional form is more often referred to simply as a polynomial form or polynomial function.
Examples of power-law functions
- The Stevens' power lawStevens' power lawStevens' power law is a proposed relationship between the magnitude of a physical stimulus and its perceived intensity or strength. It is often considered to supersede the Weber–Fechner law on the basis that it describes a wider range of sensations, although critics argue that the validity of the...
of psychophysics - The Stefan–Boltzmann law
- The Ramberg–Osgood stress–strain relationship
- The input-voltage–output-current curves of field-effect transistorField-effect transistorThe field-effect transistor is a transistor that relies on an electric field to control the shape and hence the conductivity of a channel of one type of charge carrier in a semiconductor material. FETs are sometimes called unipolar transistors to contrast their single-carrier-type operation with...
s and vacuum tubes approximate a square-law relationship, a factor in "tube soundTube soundTube sound is the characteristic sound associated with a vacuum tube-based audio amplifier. The audible significance of tube amplification on audio signals is a subject of continuing debate among audio enthusiasts....
". - A 3/2-power law can be found in the plate characteristic curves of triodeTriodeA triode is an electronic amplification device having three active electrodes. The term most commonly applies to a vacuum tube with three elements: the filament or cathode, the grid, and the plate or anode. The triode vacuum tube was the first electronic amplification device...
s. - The inverse-square lawInverse-square lawIn physics, an inverse-square law is any physical law stating that a specified physical quantity or strength is inversely proportional to the square of the distance from the source of that physical quantity....
s of Newtonian gravity and electrostaticsElectrostaticsElectrostatics is the branch of physics that deals with the phenomena and properties of stationary or slow-moving electric charges.... - Electrostatic potential and gravitational potential
- Model of van der Waals forceVan der Waals forceIn physical chemistry, the van der Waals force , named after Dutch scientist Johannes Diderik van der Waals, is the sum of the attractive or repulsive forces between molecules other than those due to covalent bonds or to the electrostatic interaction of ions with one another or with neutral...
- Force and potential in simple harmonic motionSimple harmonic motionSimple harmonic motion can serve as a mathematical model of a variety of motions, such as the oscillation of a spring. Additionally, other phenomena can be approximated by simple harmonic motion, including the motion of a simple pendulum and molecular vibration....
- Kepler's third law
- The initial mass functionInitial mass functionThe initial mass function is an empirical function that describes the mass distribution of a population of stars in terms of their theoretical initial mass...
- Gamma correctionGamma correctionGamma correction, gamma nonlinearity, gamma encoding, or often simply gamma, is the name of a nonlinear operation used to code and decode luminance or tristimulus values in video or still image systems...
relating light intensity with voltage - Kleiber's lawKleiber's lawKleiber's law, named after Max Kleiber's biological work in the early 1930s, is the observation that, for the vast majority of animals, an animal's metabolic rate scales to the ¾ power of the animal's mass. Symbolically: if q0 is the animal's metabolic rate, and M the animal's mass, then Kleiber's...
relating animal metabolism to size, and allometric laws in general - Behaviour near second-order phase transitions involving critical exponentCritical exponentCritical exponents describe the behaviour of physical quantities near continuous phase transitions. It is believed, though not proven, that they are universal, i.e...
s - Proposed form of experience curve effects
- The differential energy spectrum of cosmic-ray nuclei
- Square-cube lawSquare-cube lawThe square-cube law is a principle, drawn from the mathematics of proportion, that is applied in engineering and biomechanics. It was first demonstrated in 1638 in Galileo's Two New Sciences...
(ratio of surface area to volume) - Constructal law
- FractalFractalA fractal has been defined as "a rough or fragmented geometric shape that can be split into parts, each of which is a reduced-size copy of the whole," a property called self-similarity...
s - The Pareto principlePareto principleThe Pareto principle states that, for many events, roughly 80% of the effects come from 20% of the causes.Business-management consultant Joseph M...
also called the "80–20 rule" - Zipf's law in corpus analysis and population distributions amongst others, where frequency of an item or event is inversely proportional to its frequency rank (i.e. the second most frequent item/event occurring half as often the most frequent item and so on).
- The safe operating areaSafe operating areaFor power semiconductor devices , the safe operating area is defined as the voltage and current conditions over which the device can be expected to operate without self-damage....
relating to maximum simultaneous current and voltage in power semiconductors.
Broken power law
A broken power law is defined with a threshold: for
for 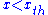 ,
,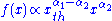 for
for 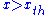 .
.Power law with exponential cutoff
A power law with an exponential cutoff is simply a power law multiplied by an exponential function: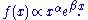
Curved power law
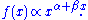
Power-law probability distributions
In the most general sense, a power-law probability distribution is a distribution whose density function (or mass function in the discrete case) has the form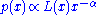
where
 , and
, and 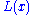 is a slowly varying function, which is any function that satisfies
is a slowly varying function, which is any function that satisfies 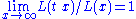 with
with  constant. This property of
constant. This property of 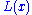 follows directly from the requirement that
follows directly from the requirement that 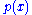 be asymptotically scale invariant; thus, the form of
be asymptotically scale invariant; thus, the form of 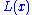 only controls the shape and finite extent of the lower tail. For instance, if
only controls the shape and finite extent of the lower tail. For instance, if  is the constant function, then we have a power-law that holds for all values of
is the constant function, then we have a power-law that holds for all values of  . In many cases, it is convenient to assume a lower bound
. In many cases, it is convenient to assume a lower bound  from which the law holds. Combining these two cases, and where
from which the law holds. Combining these two cases, and where  is a continuous variable, the power law has the form
is a continuous variable, the power law has the form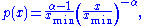
where the pre-factor to
 is the normalizing constant
is the normalizing constantNormalizing constant
The concept of a normalizing constant arises in probability theory and a variety of other areas of mathematics.-Definition and examples:In probability theory, a normalizing constant is a constant by which an everywhere non-negative function must be multiplied so the area under its graph is 1, e.g.,...
. We can now consider several properties of this distribution. For instance, its moments
Moment (mathematics)
In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...
are given by
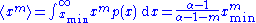
which is only well defined for
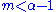 . That is, all moments
. That is, all moments 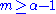 diverge: when
diverge: when  , the average and all higher-order moments are infinite; when
, the average and all higher-order moments are infinite; when 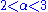 , the mean exists, but the variance and higher-order moments are infinite, etc. For finite-size samples drawn from such distribution, this behavior implies that the central moment
, the mean exists, but the variance and higher-order moments are infinite, etc. For finite-size samples drawn from such distribution, this behavior implies that the central momentCentral moment
In probability theory and statistics, central moments form one set of values by which the properties of a probability distribution can be usefully characterised...
estimators (like the mean and the variance) for diverging moments will never converge - as more data is accumulated, they continue to grow. These power-law probability distributions are also called Pareto-type distributions, distributions with Pareto tails, or distributions with regularly varying tails.
Another kind of power-law distribution, which does not satisfy the general form above, is the power law with an exponential cutoff

In this distribution, the exponential decay term
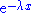 eventually overwhelms the power-law behavior at very large values of
eventually overwhelms the power-law behavior at very large values of  . This distribution does not scale and is thus not asymptotically a power law; however, it does approximately scale over a finite region before the cutoff. (Note that the pure form above is a subset of this family, with
. This distribution does not scale and is thus not asymptotically a power law; however, it does approximately scale over a finite region before the cutoff. (Note that the pure form above is a subset of this family, with  .) This distribution is a common alternative to the asymptotic power-law distribution because it naturally captures finite-size effects. For instance, although the Gutenberg–Richter law is commonly cited as an example of a power-law distribution, the distribution of earthquake magnitudes cannot scale as a power law in the limit
.) This distribution is a common alternative to the asymptotic power-law distribution because it naturally captures finite-size effects. For instance, although the Gutenberg–Richter law is commonly cited as an example of a power-law distribution, the distribution of earthquake magnitudes cannot scale as a power law in the limit 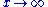 because there is a finite amount of energy in the Earth's crust and thus there must be some maximum size to an earthquake. As the scaling behavior approaches this size, it must taper off.
because there is a finite amount of energy in the Earth's crust and thus there must be some maximum size to an earthquake. As the scaling behavior approaches this size, it must taper off.Graphical methods for the identification of power-law probability distributions from random samples
Although more sophisticated and robust methods have been proposed, the most frequently used graphical methods of identifying power-law probability distributions using random samples are Pareto quantile-quantile plots (or Pareto Q-Q plotQ-Q plot
In statistics, a Q-Q plot is a probability plot, which is a graphical method for comparing two probability distributions by plotting their quantiles against each other. First, the set of intervals for the quantiles are chosen...
s), mean residual life plots (see, e.g., the books by Beirlant et al. and Coles ) and log-log plots. Another, more robust graphical method uses bundles of residual quantile functions. (Please keep in mind that power-law distributions are also called Pareto-type distributions.) It is assumed here that a random sample is obtained from a probability distribution, and that we want to know if the tail of the distribution follows a power-law (in other words, we want to know if the distribution has a "Pareto tail"). Here, the random sample is called "the data".
Pareto Q-Q plots compare the quantiles of the log-transformed data to the corresponding quantiles of an exponential distribution with mean 1 (or to the quantiles of a standard Pareto distribution) by plotting the former versus the latter. If the resultant scatterplot suggests that the plotted points " asymptotically converge" to a straight line, then a power-law distribution should be suspected. A limitation of Pareto Q-Q plots is that they behave poorly when the tail index
 (also called Pareto index) is close to 0, because Pareto Q-Q plots are not designed to identify distributions with slowly varying tails.
(also called Pareto index) is close to 0, because Pareto Q-Q plots are not designed to identify distributions with slowly varying tails.On the other hand, in its version for identifying power-law probability distributions, the mean residual life plot consists of first log-transforming the data, and then plotting the average of those log-transformed data that are higher than the i-th order statistic versus the i-th order statistic, for all i=1,...,n, where n is the size of the random sample. If the resultant scatterplot suggests that the plotted points tend to "stabilize" about a horizontal straight line, then a power-law distribution should be suspected. Since the mean residual life plot is very sensitive to outliers (it is not robust), it usually produces plots that are difficult to interpret; for this reason, such plots are usually called Hill horror plots
Log-log plots are an alternative way of graphically examining the tail of a distribution using a random sample. This method consists of plotting the logarithm of an estimator of the probability that a particular number of the distribution occurs versus the logarithm of that particular number. Usually, this estimator is the proportion of times that the number occurs in the data set. If the points in the plot tend to "converge" to a straight line for large numbers in the x axis, then the researcher concludes that the distribution has a power-law tail. An example of the application of these types of plot can be found, for instance, in Jeong et al. A disadvantage of this plots is that, in order for them to provide reliable results, they require huge amounts of data. In addition, they are appropriate only for discrete (or grouped) data.
Another graphical method for the identification of power-law probability distributions using random samples has been proposed. This methodology consists of plotting a bundle for the log-transformed sample. Originally proposed as a tool to explore the existence of moments and the moment generation function using random samples, the bundle methodology is based on residual quantile functions (RQFs), also called residual percentile functions, which provide a full characterization of the tail behavior of many well-known probability distributions, including power-law distributions, distributions with other types of heavy tails, and even non-heavy-tailed distributions. Bundle plots do not have the disadvantages of Pareto Q-Q plots, mean residual life plots and log-log plots mentioned above (they are robust to outliers, allow visually identifying power-laws with small values of
 , and do not demand the collection of much data). In addition, other types of tail behavior can be identified using bundle plots.
, and do not demand the collection of much data). In addition, other types of tail behavior can be identified using bundle plots.Plotting power-law distributions
In general, power-law distributions are plotted on doubly logarithmic axesLog-log graph
In science and engineering, a log-log graph or log-log plot is a two-dimensional graph of numerical data that uses logarithmic scales on both the horizontal and vertical axes...
, which emphasizes the upper tail region. The most convenient way to do this is via the (complementary) cumulative distribution (cdf),
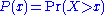 ,
,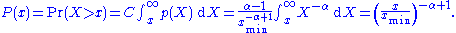
Note that the cdf is also a power-law function, but with a smaller scaling exponent. For data, an equivalent form of the cdf is the rank-frequency approach, in which we first sort the
 observed values in ascending order, and plot them against the vector
observed values in ascending order, and plot them against the vector 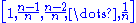 .
.Although it can be convenient to log-bin the data, or otherwise smooth the probability density (mass) function directly, these methods introduce an implicit bias in the representation of the data, and thus should be avoided. The cdf, on the other hand, introduces no bias in the data and preserves the linear signature on doubly logarithmic axes.
Estimating the exponent from empirical data
There are many ways of estimating the value of the scaling exponent for a power-law tail, however not all of them yield unbiased and consistent answers. Some of the most reliable techniques are often based on the method of maximum likelihood. Alternative methods are often based on making a linear regression on either the log-log probability, the log-log cumulative distribution function, or on log-binned data, but these approaches should be avoided as they can all lead to highly biased estimates of the scaling exponent (see the Clauset et al. reference below).Maximum likelihood
For real-valued, independent and identically distributed data, we fit a power-law distribution of the formto the data
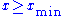 , where the coefficient
, where the coefficient 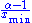 is included to ensure that the distribution is normalized
is included to ensure that the distribution is normalizedNormalizing constant
The concept of a normalizing constant arises in probability theory and a variety of other areas of mathematics.-Definition and examples:In probability theory, a normalizing constant is a constant by which an everywhere non-negative function must be multiplied so the area under its graph is 1, e.g.,...
. Given a choice for
 , a simple derivation by this method yields the estimator equation
, a simple derivation by this method yields the estimator equation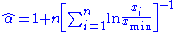
where
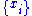 are the
are the  data points
data points  . (For a more detailed derivation, see Hall or Newman below.) This estimator exhibits a small finite sample-size bias of order
. (For a more detailed derivation, see Hall or Newman below.) This estimator exhibits a small finite sample-size bias of order 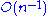 , which is small when n > 100. Further, the uncertainty in the estimation can be derived from the maximum likelihood argument, and has the form
, which is small when n > 100. Further, the uncertainty in the estimation can be derived from the maximum likelihood argument, and has the form 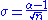 . This estimator is equivalent to the popular Hill estimator from quantitative finance and extreme value theory
. This estimator is equivalent to the popular Hill estimator from quantitative finance and extreme value theoryExtreme value theory
Extreme value theory is a branch of statistics dealing with the extreme deviations from the median of probability distributions. The general theory sets out to assess the type of probability distributions generated by processes...
.
For a set of n integer-valued data points
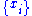 , again where each
, again where each 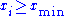 , the maximum likelihood exponent is the solution to the transcendental equation
, the maximum likelihood exponent is the solution to the transcendental equationwhere
 is the incomplete zeta function. The uncertainty in this estimate follows the same formula as for the continuous equation. However, the two equations for
is the incomplete zeta function. The uncertainty in this estimate follows the same formula as for the continuous equation. However, the two equations for 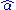 are not equivalent, and the continuous version should not be applied to discrete data, nor vice versa.
are not equivalent, and the continuous version should not be applied to discrete data, nor vice versa.Further, both of these estimators require the choice of
 . For functions with a non-trivial
. For functions with a non-trivial 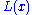 function, choosing
function, choosing  too small produces a significant bias in
too small produces a significant bias in 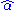 , while choosing it too large increases the uncertainty in
, while choosing it too large increases the uncertainty in 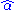 , and reduces the statistical power
, and reduces the statistical powerStatistical power
The power of a statistical test is the probability that the test will reject the null hypothesis when the null hypothesis is actually false . The power is in general a function of the possible distributions, often determined by a parameter, under the alternative hypothesis...
of our model. In general, the best choice of
 depends strongly on the particular form of the lower tail, represented by
depends strongly on the particular form of the lower tail, represented by 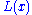 above.
above.More about these methods, and the conditions under which they can be used, can be found in the Clauset et al. reference below. Further, this comprehensive review article provides usable code (Matlab, R and C++) for estimation and testing routines for power-law distributions.
Kolmogorov–Smirnov estimation
Another method for the estimation of the power law exponent, which does not assume independent and identically distributed (iid) data, uses the minimization of the Kolmogorov–Smirnov statistic, , between the cumulative distribution functions of the data and the power law:
, between the cumulative distribution functions of the data and the power law:with
where
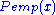 and
and 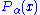 denote the cdfs of the data and the power law with exponent
denote the cdfs of the data and the power law with exponent  , respectively. As this method does not assume iid data, it provides an alternative way to determine the power law exponent for data sets in which the temporal correlation can not be ignored.
, respectively. As this method does not assume iid data, it provides an alternative way to determine the power law exponent for data sets in which the temporal correlation can not be ignored.Two point fitting method
This criterion can be applied for the estimation of power law exponent in the case of scale free distributions and provides a more convergent estimate than the maximum likelihood method. The method is described in Guerriero et al. (2011) where it has been applied to study probability distributions of fracture aperture. In some contexts the probability distribution is described, not by the cumulative distribution functionCumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
, by the cumulative frequency
Cumulative frequency analysis
Cumulative frequency analysis is the applcation of estimation theory to exceedance probability . The complement, the non-exceedance probability concerns the frequency of occurrence of values of a phenomenon staying below a reference value. The phenomenon may be time or space dependent...
of a property X, defined as the number of elements per meter (or area unit, second etc.) for which X > x applies, where x is a variable real number. As an example, the cumulative distribution of the fracture aperture, X, for a sample of N elements is defined as 'the number of fractures per meter having aperture greater than x '. Use of cumulative frequency has some advantages, e.g. it allows one to put on the same diagram data gathered from sample lines of different lengths at different scales (e.g. from outcrop and from microscope).
Examples of power-law distributions
- Pareto distribution (continuous)
- Zeta distribution (discrete)
- Yule–Simon distribution (discrete)
- Student's t-distribution (continuous), of which the Cauchy distributionCauchy distributionThe Cauchy–Lorentz distribution, named after Augustin Cauchy and Hendrik Lorentz, is a continuous probability distribution. As a probability distribution, it is known as the Cauchy distribution, while among physicists, it is known as the Lorentz distribution, Lorentz function, or Breit–Wigner...
is a special case - Zipf's law and its generalization, the Zipf–Mandelbrot law (discrete)
- The scale-free networkScale-free networkA scale-free network is a network whose degree distribution follows a power law, at least asymptotically. That is, the fraction P of nodes in the network having k connections to other nodes goes for large values of k as...
model - BibliogramBibliogramA bibliogram is a verbal construct made when noun phrases from extended stretches of text are ranked high to low by their frequency of co-occurrence with one or more user-supplied seed terms...
s - Neuronal avalanches
- HortonRobert E. HortonRobert Elmer Horton was an American ecologist and soil scientist, considered by many to be the father of modern hydrology....
's laws describing river systems - Richardson's Law for the severity of violent conflicts (wars and terrorism)
- Population of cities
- Numbers of religious adherents
- Frequency of words in a text
- Pink noisePink noisePink noise or 1/ƒ noise is a signal or process with a frequency spectrum such that the power spectral density is inversely proportional to the frequency. In pink noise, each octave carries an equal amount of noise power...
- 90–9–1 principle on wikiWikiA wiki is a website that allows the creation and editing of any number of interlinked web pages via a web browser using a simplified markup language or a WYSIWYG text editor. Wikis are typically powered by wiki software and are often used collaboratively by multiple users. Examples include...
s
A great many power-law distributions have been conjectured in recent years. For instance, power laws are thought to characterize the behavior of the upper tails for the popularity of websites, the degree distribution of the webgraph
Webgraph
The webgraph describes the directed links between pages of the World Wide Web. A graph, in general, consists of several vertices, some pairs connected by edges. In a directed graph, edges are directed lines or arcs...
, describing the hyperlink
Hyperlink
In computing, a hyperlink is a reference to data that the reader can directly follow, or that is followed automatically. A hyperlink points to a whole document or to a specific element within a document. Hypertext is text with hyperlinks...
structure of the WWW, the net worth of individuals, the number of species per genus, the popularity of given names, Gutenberg–Richter law of earthquake
Earthquake
An earthquake is the result of a sudden release of energy in the Earth's crust that creates seismic waves. The seismicity, seismism or seismic activity of an area refers to the frequency, type and size of earthquakes experienced over a period of time...
magnitudes, the size of financial returns, and many others. However, much debate remains as to which of these tails are actually power-law distributed and which are not. For instance, it is commonly accepted now that the famous Gutenberg–Richter law decays more rapidly than a pure power-law tail because of a finite exponential cutoff in the upper tail.
Validating power laws
Although power-law relations are attractive for many theoretical reasons, demonstrating that data do indeed follow a power-law relation requires more than simply fitting a particular model to the data. In general, many alternative functional forms can appear to follow a power-law form for some extent (see the Laherrere and Sornette reference below). Also, researchers usually have to face the problem of deciding whether or not a real-world probability distribution follows a power law. As a solution to this problem, Diaz proposed a graphical methodology based on random samples that allow visually discerning between different types of tail behavior. This methodology uses bundles of residual quantile functions, also called percentile residual life functions, which characterize many different types of distribution tails, including both heavy and non-heavy tails.A method for validation of power-law relations is by testing many orthogonal predictions of a particular generative mechanism against data. Simply fitting a power-law relation to a particular kind of data is not considered a rational approach. As such, the validation of power-law claims remains a very active field of research in many areas of modern science.
See also
- Empirical relationshipEmpirical relationshipIn science, an empirical relationship is one based solely on observation rather than theory. An empirical relationship requires only confirmatory data irrespective of theoretical basis. Sometimes theoretical explanations for what were initially empirical relationships are found, in which case the...
- Fat tailFat tailA fat-tailed distribution is a probability distribution that has the property, along with the heavy-tailed distributions, that they exhibit extremely large skewness or kurtosis. This comparison is often made relative to the ubiquitous normal distribution, which itself is an example of an...
- Finite-time singularity
- Fractional dynamicsFractional dynamicsFractional dynamics is a field of study in physics, mechanics, mathematics, and economics investigating the behavior of objects and systems that are described byusing integrations and differentiation of fractional orders, by methods of fractional calculus....
- Heavy-tailed distributionHeavy-tailed distributionIn probability theory, heavy-tailed distributions are probability distributions whose tails are not exponentially bounded: that is, they have heavier tails than the exponential distribution...
s - Hyperbolic growthHyperbolic growthWhen a quantity grows towards a singularity under a finite variation it is said to undergo hyperbolic growth.More precisely, the reciprocal function 1/x has a hyperbola as a graph, and has a singularity at 0, meaning that the limit as x \to 0 is infinity: any similar graph is said to exhibit...
- Lévy flightLévy flightA Lévy flight is a random walk in which the step-lengths have a probability distribution that is heavy-tailed. When defined as a walk in a space of dimension greater than one, the steps made are in isotropic random directions...
- Lognormal distribution
- Long TailLong tailLong tail may refer to:*The Long Tail, a consumer demographic in business*Power law's long tail, a statistics term describing certain kinds of distribution*Long-tail boat, a type of watercraft native to Southeast Asia...
- Power law fluid
- Simon modelSimon model-Motivation:Aiming to account for the wide range of empirical distributions following a power-law, Herbert Simon proposed a class of stochastic models that results in a power-law distribution function. It models the dynamics of a system...
- stable distribution
- Stevens' power lawStevens' power lawStevens' power law is a proposed relationship between the magnitude of a physical stimulus and its perceived intensity or strength. It is often considered to supersede the Weber–Fechner law on the basis that it describes a wider range of sensations, although critics argue that the validity of the...
- Wealth condensation
- Allometric law
- Extreme value theoryExtreme value theoryExtreme value theory is a branch of statistics dealing with the extreme deviations from the median of probability distributions. The general theory sets out to assess the type of probability distributions generated by processes...
- Kleiber's lawKleiber's lawKleiber's law, named after Max Kleiber's biological work in the early 1930s, is the observation that, for the vast majority of animals, an animal's metabolic rate scales to the ¾ power of the animal's mass. Symbolically: if q0 is the animal's metabolic rate, and M the animal's mass, then Kleiber's...
- Zipf's law
- WebgraphWebgraphThe webgraph describes the directed links between pages of the World Wide Web. A graph, in general, consists of several vertices, some pairs connected by edges. In a directed graph, edges are directed lines or arcs...
External links
- Zipf's law
- Zipf, Power-laws, and Pareto - a ranking tutorial
- Gutenberg-Richter Law
- Stream Morphometry and Horton's Laws
- Clay ShirkyClay ShirkyClay Shirky is an American writer, consultant and teacher on the social and economic effects of Internet technologies. He has a joint appointment at New York University as a Distinguished Writer in Residence at the Arthur L. Carter Journalism Institute and Assistant Arts Professor in the New...
on Institutions & Collaboration: Power law in relation to the internet-based social networks - Clay ShirkyClay ShirkyClay Shirky is an American writer, consultant and teacher on the social and economic effects of Internet technologies. He has a joint appointment at New York University as a Distinguished Writer in Residence at the Arthur L. Carter Journalism Institute and Assistant Arts Professor in the New...
on Power Laws, Weblogs, and Inequality - "How the Finance Gurus Get Risk All Wrong" by Benoit Mandelbrot & Nassim Nicholas Taleb. Fortune, July 11, 2005.
- "Million-dollar Murray": power-law distributions in homelessness and other social problems; by Malcolm Gladwell. The New Yorker, February 13, 2006.
- Benoit Mandelbrot & Richard Hudson: The Misbehaviour of Markets (2004)
- Philip Ball: Critical Mass: How one thing leads to another (2005)
- Tyranny of the Power Law from The Econophysics Blog
- So You Think You Have a Power Law — Well Isn't That Special? from Three-Toed Sloth, the blog of Cosma ShaliziCosma ShaliziCosma Rohilla Shalizi is an assistant professor in the Department of Statistics at Carnegie Mellon University in Pittsburgh....
, Professor of Statistics at Carnegie-Mellon University. - Simple MATLAB script which bins data to illustrate power-law distributions (if any) in the data.
- The Erdős Webgraph Server visualizes the distribution of the degrees of the webgraph on the download page.