Log-logistic distribution
Encyclopedia
In probability
and statistics
, the log-logistic distribution (known as the Fisk distribution in economics
) is a continuous probability distribution for a non-negative random variable
. It is used in survival analysis
as a parametric model
for events whose rate increases initially and decreases later, for example mortality from cancer following diagnosis or treatment. It has also been used in hydrology
to model stream flow and precipitation, and in economics
as a simple model of the distribution of wealth
or income
.
The log-logistic distribution is the probability distribution of a random variable
whose logarithm
has a logistic distribution.
It is similar in shape to the log-normal distribution but has heavier tails. Its cumulative distribution function
can be written in closed form, unlike that of the log-normal.
.
The parameter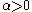
is a scale parameter
and is also the median
of the distribution. The parameter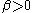
is a shape parameter
. The distribution is unimodal when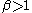
and its dispersion
decreases as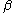
increases.
The cumulative distribution function
is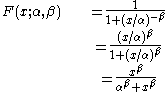
where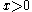
, 
, 
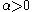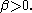
The probability density function
is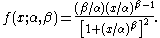
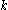th raw moment
exists only when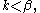
when it is given by
where B is the beta function.
Expressions for the mean
, variance
, skewness
and kurtosis
can be derived from this. Writing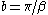
for convenience, the mean is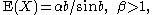
and the variance is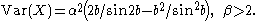
Explicit expressions for the skewness and kurtosis are lengthy.
As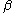
tends to infinity the mean tends to 
, the variance and skewness tend to zero and the excess kurtosis tends to 6/5 (see also related distributions below).
(inverse cumulative distribution function) is :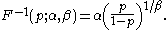
It follows that the median
is
,
the lower quartile
is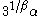
and the upper quartile is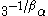
.
for survival analysis
. Unlike the more commonly-used Weibull distribution, it can have a non-monotonic hazard function: when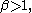
the hazard function is unimodal (when 
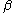≤ 1, the hazard decreases monotonically). The fact that the cumulative distribution function can be written in closed form is particularly useful for analysis of survival data with censoring.
The log-logistic distribution can be used as the basis of an accelerated failure time model
by allowing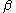
to differ between groups, or more generally by introducing covariates that affect 
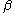but not 
by modelling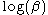 
as a linear function of the covariates.
The survival function
is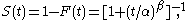
and so the hazard function is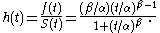
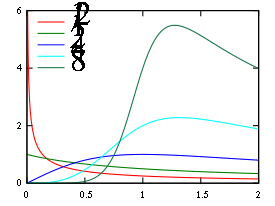
Extreme values like maximum one-day rainfall and river discharge per month or per year often follow a log-normal distribution. The log-normal distribution, however, needs a numeric approximation. As the log-logistic distribution, which can be solved analytically, is similar to the log-normal distribution, it can be used instead.
The blue picture illustrates an example of fitting the log-logistic distribution to ranked maximum one-day October rainfalls and it shows the 90% confidence belt based on the binomial distribution. The rainfall data are represented by the plotting position r/(n+1) as part of the cumulative frequency analysis
.
or income
in economics
, where it is known as the Fisk distribution.
Its Gini coefficient
is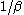
.
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
and statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the log-logistic distribution (known as the Fisk distribution in economics
Economics
Economics is the social science that analyzes the production, distribution, and consumption of goods and services. The term economics comes from the Ancient Greek from + , hence "rules of the house"...
) is a continuous probability distribution for a non-negative random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
. It is used in survival analysis
Survival analysis
Survival analysis is a branch of statistics which deals with death in biological organisms and failure in mechanical systems. This topic is called reliability theory or reliability analysis in engineering, and duration analysis or duration modeling in economics or sociology...
as a parametric model
Parametric model
In statistics, a parametric model or parametric family or finite-dimensional model is a family of distributions that can be described using a finite number of parameters...
for events whose rate increases initially and decreases later, for example mortality from cancer following diagnosis or treatment. It has also been used in hydrology
Hydrology
Hydrology is the study of the movement, distribution, and quality of water on Earth and other planets, including the hydrologic cycle, water resources and environmental watershed sustainability...
to model stream flow and precipitation, and in economics
Economics
Economics is the social science that analyzes the production, distribution, and consumption of goods and services. The term economics comes from the Ancient Greek from + , hence "rules of the house"...
as a simple model of the distribution of wealth
Distribution of wealth
The distribution of wealth is a comparison of the wealth of various members or groups in a society. It differs from the distribution of income in that it looks at the distribution of ownership of the assets in a society, rather than the current income of members of that society.-Definition of...
or income
Income distribution
In economics, income distribution is how a nation’s total economy is distributed amongst its population.Income distribution has always been a central concern of economic theory and economic policy...
.
The log-logistic distribution is the probability distribution of a random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
whose logarithm
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
has a logistic distribution.
It is similar in shape to the log-normal distribution but has heavier tails. Its cumulative distribution function
Cumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
can be written in closed form, unlike that of the log-normal.
Characterisation
There are several different parameterizations of the distribution in use. The one shown here gives reasonably interpretable parameters and a simple form for the cumulative distribution functionCumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
.
The parameter
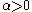is a scale parameterScale parameter
In probability theory and statistics, a scale parameter is a special kind of numerical parameter of a parametric family of probability distributions...
and is also the median
Median
In probability theory and statistics, a median is described as the numerical value separating the higher half of a sample, a population, or a probability distribution, from the lower half. The median of a finite list of numbers can be found by arranging all the observations from lowest value to...
of the distribution. The parameter
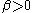is a shape parameterShape parameter
In probability theory and statistics, a shape parameter is a kind of numerical parameter of a parametric family of probability distributions.- Definition :...
. The distribution is unimodal when
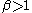and its dispersionDispersion
Dispersion may refer to:In physics:*The dependence of wave velocity on frequency or wavelength:**Dispersion , for light waves**Dispersion **Acoustic dispersion, for sound waves...
decreases as
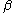increases.The cumulative distribution function
Cumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
is
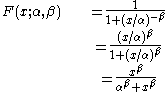
where
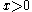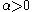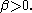
, , The probability density function
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
is
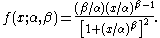
Moments
The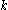th raw momentMoment (mathematics)
In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...
exists only when
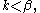when it is given bywhere B is the beta function.
Expressions for the mean
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
, variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
, skewness
Skewness
In probability theory and statistics, skewness is a measure of the asymmetry of the probability distribution of a real-valued random variable. The skewness value can be positive or negative, or even undefined...
and kurtosis
Kurtosis
In probability theory and statistics, kurtosis is any measure of the "peakedness" of the probability distribution of a real-valued random variable...
can be derived from this. Writing
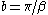for convenience, the mean is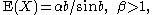and the variance is
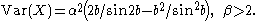
Explicit expressions for the skewness and kurtosis are lengthy.
As
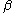tends to infinity the mean tends to , the variance and skewness tend to zero and the excess kurtosis tends to 6/5 (see also related distributions below).Quantiles
The quantile functionQuantile function
In probability and statistics, the quantile function of the probability distribution of a random variable specifies, for a given probability, the value which the random variable will be at, or below, with that probability...
(inverse cumulative distribution function) is :
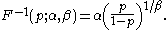
It follows that the median
Median
In probability theory and statistics, a median is described as the numerical value separating the higher half of a sample, a population, or a probability distribution, from the lower half. The median of a finite list of numbers can be found by arranging all the observations from lowest value to...
is
,the lower quartile
Quartile
In descriptive statistics, the quartiles of a set of values are the three points that divide the data set into four equal groups, each representing a fourth of the population being sampled...
is
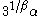
and the upper quartile is
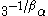.Applications
Survival analysis
The log-logistic distribution provides one parametric modelParametric model
In statistics, a parametric model or parametric family or finite-dimensional model is a family of distributions that can be described using a finite number of parameters...
for survival analysis
Survival analysis
Survival analysis is a branch of statistics which deals with death in biological organisms and failure in mechanical systems. This topic is called reliability theory or reliability analysis in engineering, and duration analysis or duration modeling in economics or sociology...
. Unlike the more commonly-used Weibull distribution, it can have a non-monotonic hazard function: when
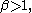the hazard function is unimodal (when 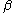≤ 1, the hazard decreases monotonically). The fact that the cumulative distribution function can be written in closed form is particularly useful for analysis of survival data with censoring.The log-logistic distribution can be used as the basis of an accelerated failure time model
Accelerated failure time model
In the statistical area of survival analysis, an accelerated failure time model is a parametric model that provides an alternative to the commonly used proportional hazards models...
by allowing
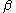to differ between groups, or more generally by introducing covariates that affect 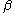but not by modelling 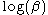as a linear function of the covariates.The survival function
Survival function
The survival function, also known as a survivor function or reliability function, is a property of any random variable that maps a set of events, usually associated with mortality or failure of some system, onto time. It captures the probability that the system will survive beyond a specified time...
is
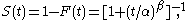
and so the hazard function is
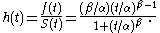
Hydrology
The log-logistic distribution has been used in hydrology for modelling stream flow rates and precipitation.Extreme values like maximum one-day rainfall and river discharge per month or per year often follow a log-normal distribution. The log-normal distribution, however, needs a numeric approximation. As the log-logistic distribution, which can be solved analytically, is similar to the log-normal distribution, it can be used instead.
The blue picture illustrates an example of fitting the log-logistic distribution to ranked maximum one-day October rainfalls and it shows the 90% confidence belt based on the binomial distribution. The rainfall data are represented by the plotting position r/(n+1) as part of the cumulative frequency analysis
Cumulative frequency analysis
Cumulative frequency analysis is the applcation of estimation theory to exceedance probability . The complement, the non-exceedance probability concerns the frequency of occurrence of values of a phenomenon staying below a reference value. The phenomenon may be time or space dependent...
.
Economics
The log-logistic has been used as a simple model of the distribution of wealthDistribution of wealth
The distribution of wealth is a comparison of the wealth of various members or groups in a society. It differs from the distribution of income in that it looks at the distribution of ownership of the assets in a society, rather than the current income of members of that society.-Definition of...
or income
Income distribution
In economics, income distribution is how a nation’s total economy is distributed amongst its population.Income distribution has always been a central concern of economic theory and economic policy...
in economics
Economics
Economics is the social science that analyzes the production, distribution, and consumption of goods and services. The term economics comes from the Ancient Greek from + , hence "rules of the house"...
, where it is known as the Fisk distribution.
Its Gini coefficient
Gini coefficient
The Gini coefficient is a measure of statistical dispersion developed by the Italian statistician and sociologist Corrado Gini and published in his 1912 paper "Variability and Mutability" ....
is
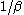.Related distributions
- If
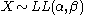then 
-
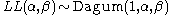(Dagum distribution) -
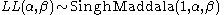(Singh-Maddala distribution) -
Beta prime distribution
- If X has a log-logistic distribution with scale parameter
and shape parameter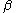 
then Y = log(X) has a logistic distribution with location parameter 
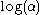and scale parameter 
.
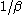- As the shape parameter
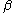of the log-logistic distribution increases, its shape increasingly resembles that of a (very narrow) logistic distribution. Informally, as 
→∞,
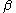- The log-logistic distribution with shape parameter
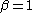and scale parameter 
is the same as the generalized Pareto distribution with location parameter 
, shape parameter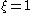 
and scale parameter 
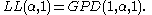
- The addition of another parameter (a shift parameter) formally results in a shifted log-logistic distribution, but this is usually considered in a different parameterization so that the distribution can be bounded above or bounded below.
Generalizations
Several different distributions are sometimes referred to as the generalized log-logistic distribution, as they contain the log-logistic as a special case. These include the Burr Type XII distribution (also known as the Singh-Maddala distribution) and the Dagum distribution, both of which include a second shape parameter. Both are in turn special cases of the even more general generalized beta distribution of the second kind. Another more straightforward generalization of the log-logistic is the shifted log-logistic distribution.
See also
- Probability distributions: List of important distributions supported on semi-infinite intervals
- The log-logistic distribution with shape parameter