Von Mises-Fisher distribution
Encyclopedia
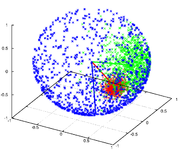
probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
on the
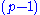-dimensional sphereSphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
in
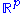. If 
the distribution reduces to the von Mises distribution on the circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
.
The probability density function of the von Mises-Fisher distribution for the random p-dimensional unit vector
is given by: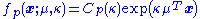
where
andthe normalization constant
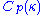is equal to-
where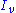
denotes the modified Bessel functionBessel functionIn mathematics, Bessel functions, first defined by the mathematician Daniel Bernoulli and generalized by Friedrich Bessel, are canonical solutions y of Bessel's differential equation:...
of the first kind and order
. If 
, the normalization constant reduces to
-
The parameters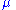
and 
are called the mean direction and concentration parameter, respectively. The greater the value of 
, the higher the concentration of the distribution around the mean direction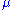 
. The distribution is unimodal for 
, and is uniform on the sphere for 
.
The von Mises-Fisher distribution for
, also called the Fisher distribution, was first used to model the interaction of dipoles in an electric field (Mardia, 2000). Other applications are found in geologyGeologyGeology is the science comprising the study of solid Earth, the rocks of which it is composed, and the processes by which it evolves. Geology gives insight into the history of the Earth, as it provides the primary evidence for plate tectonics, the evolutionary history of life, and past climates...
, bioinformaticsBioinformaticsBioinformatics is the application of computer science and information technology to the field of biology and medicine. Bioinformatics deals with algorithms, databases and information systems, web technologies, artificial intelligence and soft computing, information and computation theory, software...
, and text miningText miningText mining, sometimes alternately referred to as text data mining, roughly equivalent to text analytics, refers to the process of deriving high-quality information from text. High-quality information is typically derived through the devising of patterns and trends through means such as...
.
Estimation of parameters
A series of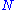
independent measurements 
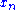are drawn from a von Mises-Fisher distribution. The solution obtained by maximizing the log-likelihood is then (Sra, 2009)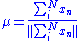
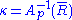
where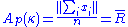
A simple approximation to
is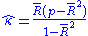
but a more accurate measure can be obtained by iterating the Newton method a few times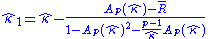
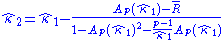
See also
- Kent distribution, a related distribution on the two-dimensional unit sphere
- von Mises distribution, von Mises–Fisher distribution where p=2, the one-dimensional unit circle
- Bivariate von Mises distributionBivariate von Mises distributionIn probability theory and statistics, the bivariate von Mises distribution is a probability distribution describing values on a torus. It may be thought of as an analogue on the torus of the bivariate normal distribution. The distribution belongs to the field of directional statistics. The general...
- Directional statistics
-