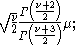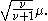Noncentral t-distribution
Encyclopedia
In probability
and statistics
, the noncentral t-distribution (also known as the singly noncentral t-distribution) generalizes Student's t-distribution using a noncentrality parameter
. Like the central t-distribution, the noncentral t-distribution is primarily used in statistical inference
, although it may also be used in robust modeling
for data
. In particular, the noncentral t-distribution arises in power analysis
.
 is a normally distributed random variable with unit variance and zero mean, and
is a normally distributed random variable with unit variance and zero mean, and  is a Chi-squared distributed random variable with
is a Chi-squared distributed random variable with 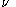 degrees of freedom
degrees of freedom
that is statistically independent
of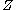 , then
, then

is a noncentral t-distributed random variable with degrees of freedom and noncentrality parameter
degrees of freedom and noncentrality parameter
 . Note that the noncentrality parameter may be negative.
. Note that the noncentrality parameter may be negative.
of noncentral t-distribution with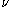 degrees of freedom and noncentrality parameter
degrees of freedom and noncentrality parameter  can be expressed as
can be expressed as
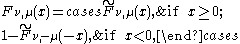
where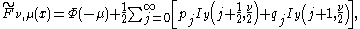
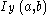 is the regularized incomplete beta function,
is the regularized incomplete beta function,
and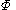 is the cumulative distribution function of the standard normal distribution.
is the cumulative distribution function of the standard normal distribution.
Alternatively, the noncentral t-distribution CDF can be expressed as: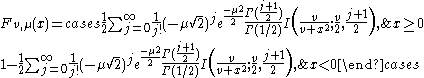
where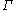 is the gamma function
is the gamma function
and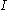 is the regularized incomplete beta function.
is the regularized incomplete beta function.
Although there are other forms of the cumulative distribution function, the first form presented above is very easy to evaluate through recursive computing
. In statistical software R
, the cumulative distribution function is implemented as pt.
for the noncentral t-distribution with degrees of freedom and noncentrality parameter
degrees of freedom and noncentrality parameter 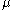 can be expressed in several forms.
can be expressed in several forms.
The confluent hypergeometric function
form of the density function is
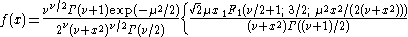
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
and statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the noncentral t-distribution (also known as the singly noncentral t-distribution) generalizes Student's t-distribution using a noncentrality parameter
Noncentrality parameter
Noncentrality parameters are parameters of families of probability distributions which are related to other "central" families of distributions. If the noncentrality parameter of a distribution is zero, the distribution is identical to a distribution in the central family...
. Like the central t-distribution, the noncentral t-distribution is primarily used in statistical inference
Statistical inference
In statistics, statistical inference is the process of drawing conclusions from data that are subject to random variation, for example, observational errors or sampling variation...
, although it may also be used in robust modeling
Robust statistics
Robust statistics provides an alternative approach to classical statistical methods. The motivation is to produce estimators that are not unduly affected by small departures from model assumptions.- Introduction :...
for data
Data
The term data refers to qualitative or quantitative attributes of a variable or set of variables. Data are typically the results of measurements and can be the basis of graphs, images, or observations of a set of variables. Data are often viewed as the lowest level of abstraction from which...
. In particular, the noncentral t-distribution arises in power analysis
Statistical power
The power of a statistical test is the probability that the test will reject the null hypothesis when the null hypothesis is actually false . The power is in general a function of the possible distributions, often determined by a parameter, under the alternative hypothesis...
.
Characterization
If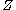 is a normally distributed random variable with unit variance and zero mean, and
is a normally distributed random variable with unit variance and zero mean, and 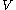 is a Chi-squared distributed random variable with
is a Chi-squared distributed random variable with 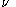 degrees of freedom
degrees of freedomDegrees of freedom (statistics)
In statistics, the number of degrees of freedom is the number of values in the final calculation of a statistic that are free to vary.Estimates of statistical parameters can be based upon different amounts of information or data. The number of independent pieces of information that go into the...
that is statistically independent
Statistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
of
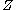 , then
, then
is a noncentral t-distributed random variable with
 degrees of freedom and noncentrality parameter
degrees of freedom and noncentrality parameterNoncentrality parameter
Noncentrality parameters are parameters of families of probability distributions which are related to other "central" families of distributions. If the noncentrality parameter of a distribution is zero, the distribution is identical to a distribution in the central family...
 . Note that the noncentrality parameter may be negative.
. Note that the noncentrality parameter may be negative.Cumulative distribution function
The cumulative distribution functionCumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
of noncentral t-distribution with
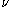 degrees of freedom and noncentrality parameter
degrees of freedom and noncentrality parameter  can be expressed as
can be expressed as 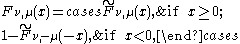
where
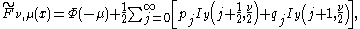
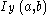 is the regularized incomplete beta function,
is the regularized incomplete beta function,
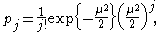
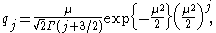
and
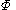 is the cumulative distribution function of the standard normal distribution.
is the cumulative distribution function of the standard normal distribution.Alternatively, the noncentral t-distribution CDF can be expressed as:
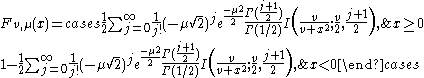
where
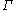 is the gamma function
is the gamma functionGamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
and
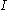 is the regularized incomplete beta function.
is the regularized incomplete beta function.Although there are other forms of the cumulative distribution function, the first form presented above is very easy to evaluate through recursive computing
Recursion
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
. In statistical software R
R (programming language)
R is a programming language and software environment for statistical computing and graphics. The R language is widely used among statisticians for developing statistical software, and R is widely used for statistical software development and data analysis....
, the cumulative distribution function is implemented as pt.
Probability density function
The probability density functionProbability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
for the noncentral t-distribution with
 degrees of freedom and noncentrality parameter
degrees of freedom and noncentrality parameter 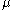 can be expressed in several forms.
can be expressed in several forms.The confluent hypergeometric function
Confluent hypergeometric function
In mathematics, a confluent hypergeometric function is a solution of a confluent hypergeometric equation, which is a degenerate form of a hypergeometric differential equation where two of the three regular singularities merge into an irregular singularity...
form of the density function is
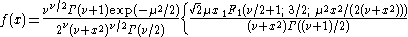
-
-
-
-
-
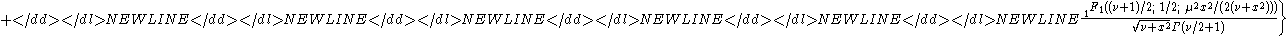
where is a confluent hypergeometric functionConfluent hypergeometric functionIn mathematics, a confluent hypergeometric function is a solution of a confluent hypergeometric equation, which is a degenerate form of a hypergeometric differential equation where two of the three regular singularities merge into an irregular singularity...
is a confluent hypergeometric functionConfluent hypergeometric functionIn mathematics, a confluent hypergeometric function is a solution of a confluent hypergeometric equation, which is a degenerate form of a hypergeometric differential equation where two of the three regular singularities merge into an irregular singularity...
.
An alternative integral form is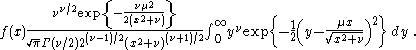
A third form of the density is obtained using its cumulative distribution functions, as follows.
This is the approach implemented by the dt function in RR (programming language)R is a programming language and software environment for statistical computing and graphics. The R language is widely used among statisticians for developing statistical software, and R is widely used for statistical software development and data analysis....
.
Moments of the Noncentral t-distribution
In general, the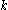 th raw moment of the non-central t-distribution is
th raw moment of the non-central t-distribution is
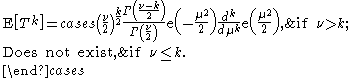
In particular, the mean and variance of the noncentral t-distribution are
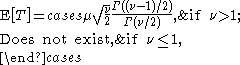
and
Asymmetry
The noncentral t-distribution is asymmetric unless μ is zero, i.e., a central t-distribution. The right tail will be heavier than the left when μ > 0, and vice versa. However, the usual skewness is not generally a good measure of asymmetry for this distribution, because if the degrees of freedom is not larger than 3, the third moment does not exist at all. Even if the degrees of freedom is greater than 3, the sample estimate of the skewness is still very unstable unless the sample size is very large.
Mode
The noncentral t-distribution is always unimodal and bell shaped, but the mode is not analytically available, although it always lies in the interval-
-
-
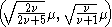 when
when 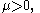 and
and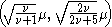 when
when 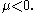
-
-
Moreover, the mode always has the same sign as the noncentrality parameter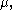 and the negative of the mode is exactly the mode for a noncentral t-distribution with the same number of degrees of freedom
and the negative of the mode is exactly the mode for a noncentral t-distribution with the same number of degrees of freedom  but noncentrality parameter
but noncentrality parameter 
The mode is strictly increasing with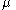 when
when 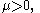 and strictly decreasing with
and strictly decreasing with 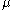 when
when 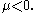 In the limit, when
In the limit, when 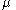 approaches zero, the mode is approximated by
approaches zero, the mode is approximated by
and when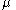 approaches infinity, the mode is approximated by
approaches infinity, the mode is approximated by
Use in power analysis
Suppose we have an independent and identically distributed sample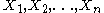 , each of which is normally distributed with mean
, each of which is normally distributed with mean 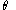 and variance
and variance 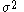 , and we are interested in testing the null hypothesisNull hypothesisThe practice of science involves formulating and testing hypotheses, assertions that are capable of being proven false using a test of observed data. The null hypothesis typically corresponds to a general or default position...
, and we are interested in testing the null hypothesisNull hypothesisThe practice of science involves formulating and testing hypotheses, assertions that are capable of being proven false using a test of observed data. The null hypothesis typically corresponds to a general or default position...
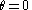 vs. the alternative hypothesis
vs. the alternative hypothesis 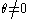 . We can perform a one sample t-testStudent's t-testA t-test is any statistical hypothesis test in which the test statistic follows a Student's t distribution if the null hypothesis is supported. It is most commonly applied when the test statistic would follow a normal distribution if the value of a scaling term in the test statistic were known...
. We can perform a one sample t-testStudent's t-testA t-test is any statistical hypothesis test in which the test statistic follows a Student's t distribution if the null hypothesis is supported. It is most commonly applied when the test statistic would follow a normal distribution if the value of a scaling term in the test statistic were known...
using the test statisticTest statisticIn statistical hypothesis testing, a hypothesis test is typically specified in terms of a test statistic, which is a function of the sample; it is considered as a numerical summary of a set of data that...
-
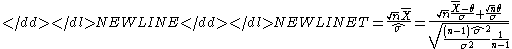
where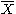 is the sample mean and
is the sample mean and 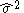 is the unbiased sample variance. Since the right hand side of the second equality exactly matches the characterization of a noncentral t-distribution as described above,
is the unbiased sample variance. Since the right hand side of the second equality exactly matches the characterization of a noncentral t-distribution as described above,  has a noncentral t-distribution with
has a noncentral t-distribution with  degrees of freedom and noncentrality parameter
degrees of freedom and noncentrality parameter 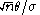 .
.
If the test procedure rejects the null hypothesis whenever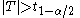 , where
, where 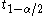 is the upper
is the upper 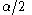 quantile of the (central) Student's t-distribution for a pre-specified
quantile of the (central) Student's t-distribution for a pre-specified  , then the power of this test is given by
, then the power of this test is given by
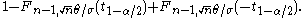
Similar applications of the noncentral t-distribution can be found in the power analysisStatistical powerThe power of a statistical test is the probability that the test will reject the null hypothesis when the null hypothesis is actually false . The power is in general a function of the possible distributions, often determined by a parameter, under the alternative hypothesis...
of the general normal-theory linear modelsGeneral linear modelThe general linear model is a statistical linear model.It may be written aswhere Y is a matrix with series of multivariate measurements, X is a matrix that might be a design matrix, B is a matrix containing parameters that are usually to be estimated and U is a matrix containing errors or...
, which includes the above one sample t-testStudent's t-testA t-test is any statistical hypothesis test in which the test statistic follows a Student's t distribution if the null hypothesis is supported. It is most commonly applied when the test statistic would follow a normal distribution if the value of a scaling term in the test statistic were known...
as a special case.
Related distributions
- Central t distribution: The central t-distribution can be converted into a locationLocation parameterIn statistics, a location family is a class of probability distributions that is parametrized by a scalar- or vector-valued parameter μ, which determines the "location" or shift of the distribution...
/scaleScale parameterIn probability theory and statistics, a scale parameter is a special kind of numerical parameter of a parametric family of probability distributions...
family. This family of distributions is used in data modeling to capture various tail behaviors. The location/scale generalization of the central t-distribution is a different distribution from the noncentral t-distribution discussed in this article. In particular, this approximation does not respect the asymmetry of the noncentral t-distribution. However, the central t-distribution can be used as an approximation to the non-central t-distribution.
- If
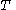 is noncentral t-distributed with
is noncentral t-distributed with 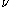 degrees of freedom and noncentrality parameter
degrees of freedom and noncentrality parameter 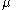 and
and  , then
, then 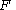 has a noncentral
has a noncentral 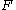 -distributionNoncentral F-distributionIn probability theory and statistics, the noncentral F-distribution is a continuous probability distribution that is a generalization of the F-distribution...
-distributionNoncentral F-distributionIn probability theory and statistics, the noncentral F-distribution is a continuous probability distribution that is a generalization of the F-distribution...
with 1 numerator degree of freedom,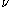 denominator degrees of freedom, and noncentrality parameter
denominator degrees of freedom, and noncentrality parameter 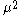 .
.
- If
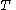 is noncentral t-distributed with
is noncentral t-distributed with 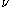 degrees of freedom and noncentrality parameter
degrees of freedom and noncentrality parameter 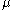 and
and  , then
, then 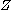 has a normal distribution with mean
has a normal distribution with mean 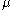 and unit variance.
and unit variance.
- When the denominator noncentrality parameter of a doubly noncentral t-distribution is zero, then it becomes a noncentral t-distribution.
Special cases
- When
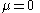 , the noncentral t-distribution becomes the central (Student's) t-distribution with the same degrees of freedom.
, the noncentral t-distribution becomes the central (Student's) t-distribution with the same degrees of freedom.
External links
- Eric W. Weisstein. "Noncentral Student's t-Distribution." From MathWorld—A Wolfram Web Resource
- Central t distribution: The central t-distribution can be converted into a location
-
-
-
-
-