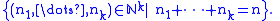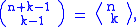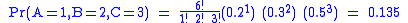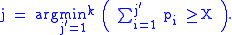Multinomial distribution
Encyclopedia
In probability theory
, the multinomial distribution is a generalization of the binomial distribution.
The binomial distribution is the probability distribution
of the number of "successes" in n independent
Bernoulli trial
s, with the same probability of "success" on each trial. In a multinomial distribution, the analog of the Bernoulli distribution is the categorical distribution
, where each trial results in exactly one of some fixed finite number k of possible outcomes, with probabilities p1, ..., pk (so that pi ≥ 0 for i = 1, ..., k and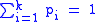 ), and there are n independent trials. Then let the random variables Xi indicate the number of times outcome number i was observed over the n trials. The vector X = (X1, ..., Xk) follows a multinomial distribution with parameters n and p, where p = (p1, ..., pk).
), and there are n independent trials. Then let the random variables Xi indicate the number of times outcome number i was observed over the n trials. The vector X = (X1, ..., Xk) follows a multinomial distribution with parameters n and p, where p = (p1, ..., pk).
Note that, in some fields, such as natural language processing
, the categorical and multinomial distributions are conflated, and it is common to speak of a "multinomial distribution" when a categorical distribution
is actually meant. This stems from the fact that it is sometimes convenient to express the outcome of a categorical distribution as a "1-of-K" vector (a vector with one element containing a 1 and all other elements containing a 0) rather than as an integer in the range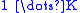 ; in this form, a categorical distribution is equivalent to a multinomial distribution over a single observation.
; in this form, a categorical distribution is equivalent to a multinomial distribution over a single observation.
of the multinomial distribution is:
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, the multinomial distribution is a generalization of the binomial distribution.
The binomial distribution is the probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
of the number of "successes" in n independent
Statistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
Bernoulli trial
Bernoulli trial
In the theory of probability and statistics, a Bernoulli trial is an experiment whose outcome is random and can be either of two possible outcomes, "success" and "failure"....
s, with the same probability of "success" on each trial. In a multinomial distribution, the analog of the Bernoulli distribution is the categorical distribution
Categorical distribution
In probability theory and statistics, a categorical distribution is a probability distribution that describes the result of a random event that can take on one of K possible outcomes, with the probability of each outcome separately specified...
, where each trial results in exactly one of some fixed finite number k of possible outcomes, with probabilities p1, ..., pk (so that pi ≥ 0 for i = 1, ..., k and
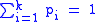 ), and there are n independent trials. Then let the random variables Xi indicate the number of times outcome number i was observed over the n trials. The vector X = (X1, ..., Xk) follows a multinomial distribution with parameters n and p, where p = (p1, ..., pk).
), and there are n independent trials. Then let the random variables Xi indicate the number of times outcome number i was observed over the n trials. The vector X = (X1, ..., Xk) follows a multinomial distribution with parameters n and p, where p = (p1, ..., pk).Note that, in some fields, such as natural language processing
Natural language processing
Natural language processing is a field of computer science and linguistics concerned with the interactions between computers and human languages; it began as a branch of artificial intelligence....
, the categorical and multinomial distributions are conflated, and it is common to speak of a "multinomial distribution" when a categorical distribution
Categorical distribution
In probability theory and statistics, a categorical distribution is a probability distribution that describes the result of a random event that can take on one of K possible outcomes, with the probability of each outcome separately specified...
is actually meant. This stems from the fact that it is sometimes convenient to express the outcome of a categorical distribution as a "1-of-K" vector (a vector with one element containing a 1 and all other elements containing a 0) rather than as an integer in the range
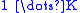 ; in this form, a categorical distribution is equivalent to a multinomial distribution over a single observation.
; in this form, a categorical distribution is equivalent to a multinomial distribution over a single observation.Probability mass function
The probability mass functionProbability mass function
In probability theory and statistics, a probability mass function is a function that gives the probability that a discrete random variable is exactly equal to some value...
of the multinomial distribution is:
-
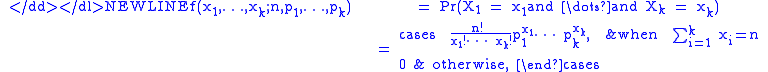
for non-negative integers x1, ..., xk.
As slices of generalized Pascal's triangle
Just like one can interpret the binomial distribution as (normalized) 1D slices of Pascal's trianglePascal's triangleIn mathematics, Pascal's triangle is a triangular array of the binomial coefficients in a triangle. It is named after the French mathematician, Blaise Pascal...
, so too can one interpret the multinomial distribution as 2D (triangular) slices of Pascal's pyramidPascal's pyramidIn mathematics, Pascal's Pyramid is a three-dimensional arrangement of the trinomial numbers, which are the coefficients of the trinomial expansion and the trinomial distribution. Pascal's Pyramid is the three-dimensional analog of the two-dimensional Pascal's triangle, which contains the binomial...
, or 3D/4D/+ (pyramid-shaped) slices of higher-dimensional analogs of Pascal's triangle. This reveals an interpretation of the rangeRange (mathematics)In mathematics, the range of a function refers to either the codomain or the image of the function, depending upon usage. This ambiguity is illustrated by the function f that maps real numbers to real numbers with f = x^2. Some books say that range of this function is its codomain, the set of all...
of the distribution: discretized equilaterial "pyramids" in arbitrary dimension -- i.e. a simplexSimplexIn geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
with a grid.
As polynomial coefficients
Similarly, just like one can interpret the binomial distribution as the polynomial coefficients of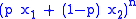 when expanded, one can interpret the multinomial distribution as the coefficients of
when expanded, one can interpret the multinomial distribution as the coefficients of 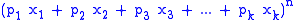 when expanded. (Note that just like the binomial distribution, the coefficients must sum to 1.) This is the origin of the name "multinomial distribution".
when expanded. (Note that just like the binomial distribution, the coefficients must sum to 1.) This is the origin of the name "multinomial distribution".
Properties
The expectedExpected valueIn probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
number of times the outcome i was observed over n trials is
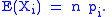
The covariance matrixCovariance matrixIn probability theory and statistics, a covariance matrix is a matrix whose element in the i, j position is the covariance between the i th and j th elements of a random vector...
is as follows. Each diagonal entry is the varianceVarianceIn probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
of a binomially distributed random variable, and is therefore
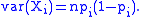
The off-diagonal entries are the covarianceCovarianceIn probability theory and statistics, covariance is a measure of how much two variables change together. Variance is a special case of the covariance when the two variables are identical.- Definition :...
s:
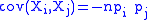
for i, j distinct.
All covariances are negative because for fixed n, an increase in one component of a multinomial vector requires a decrease in another component.
This is a k × k positive-semidefinite matrix of rank k − 1.
The off-diagonal entries of the corresponding correlation matrix are
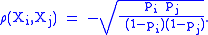
Note that the sample size drops out of this expression.
Each of the k components separately has a binomial distribution with parameters n and pi, for the appropriate value of the subscript i.
The supportSupport (mathematics)In mathematics, the support of a function is the set of points where the function is not zero, or the closure of that set . This concept is used very widely in mathematical analysis...
of the multinomial distribution is the set
Its number of elements is
the number of n-combinations of a multisetMultisetIn mathematics, the notion of multiset is a generalization of the notion of set in which members are allowed to appear more than once...
with k types, or multiset coefficient.
Example
In a recent three-way election for a large country, candidate A received 20% of the votes, candidate B received 30% of the votes, and candidate C received 50% of the votes. If six voters are selected randomly, what is the probability that there will be exactly one supporter for candidate A, two supporters for candidate B and three supporters for candidate C in the sample?
Note: Since we’re assuming that the voting population is large, it is reasonable and permissible to think of the probabilities as unchanging once a voter is selected for the sample. Technically speaking this is sampling without replacement, so the correct distribution is the multivariate hypergeometric distribution, but the distributions converge as the population grows large.
Sampling from a multinomial distribution
First, reorder the parameters such that they are sorted in descending order (this is only to speed up computation and not strictly necessary). Now, for each trial, draw an auxiliary variable X from a uniform (0, 1) distribution. The resulting outcome is the component
such that they are sorted in descending order (this is only to speed up computation and not strictly necessary). Now, for each trial, draw an auxiliary variable X from a uniform (0, 1) distribution. The resulting outcome is the component
This is a sample for the multinomial distribution with n = 1. A sum of independent repetitions of this experiment is a sample from a multinomial distribution with n equal to the number of such repetitions.
Related distributions
- When k = 2, the multinomial distribution is the binomial distribution.
- The continuous analogue is Multivariate normal distribution.
- Categorical distributionCategorical distributionIn probability theory and statistics, a categorical distribution is a probability distribution that describes the result of a random event that can take on one of K possible outcomes, with the probability of each outcome separately specified...
, the distribution of each trial; for k = 2, this is the Bernoulli distribution. - The Dirichlet distribution is the conjugate priorConjugate priorIn Bayesian probability theory, if the posterior distributions p are in the same family as the prior probability distribution p, the prior and posterior are then called conjugate distributions, and the prior is called a conjugate prior for the likelihood...
of the multinomial in Bayesian statisticsBayesian statisticsBayesian statistics is that subset of the entire field of statistics in which the evidence about the true state of the world is expressed in terms of degrees of belief or, more specifically, Bayesian probabilities...
. - Multivariate Pólya distributionMultivariate Polya distributionThe multivariate Pólya distribution, named after George Pólya, also called the Dirichlet compound multinomial distribution, is a compound probability distribution, where a probability vector p is drawn from a Dirichlet distribution with parameter vector \alpha, and a set of discrete samples is...
. - Beta-binomial model.
See also
- Fisher's exact testFisher's exact testFisher's exact test is a statistical significance test used in the analysis of contingency tables where sample sizes are small. It is named after its inventor, R. A...
- Multinomial theoremMultinomial theoremIn mathematics, the multinomial theorem says how to expand a power of a sum in terms of powers of the terms in that sum. It is the generalization of the binomial theorem to polynomials.-Theorem:...
- Negative multinomial distribution
-