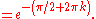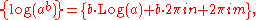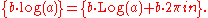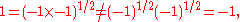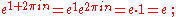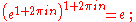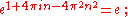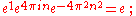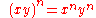Exponentiation
Encyclopedia
Exponentiation is a mathematical
operation
, written as an, involving two numbers, the base
a and the exponent (or power) n. When n is a positive integer, exponentiation corresponds to repeated multiplication
; in other words, a product of n factors of a (the product itself can also be called power):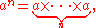
just as multiplication by a positive integer corresponds to repeated addition
:
The exponent is usually shown as a superscript to the right of the base. The exponentiation an can be read as: a raised to the n-th power, a raised to the power [of] n, or possibly a raised to the exponent [of] n, or more briefly as a to the n. Some exponents have their own pronunciation: for example, a2 is usually read as a squared and a3 as a cubed. When superscripts cannot be used, as in plain ASCII text
, common alternative formats include a^n and a**n.
The power an can be defined also when n is a negative integer, for nonzero a.
No natural extension to all real a and n exists,
but when the base a is a positive real number, an can be defined for all real and even complex exponents n via the exponential function
ez. Trigonometric functions
can be expressed in terms of complex exponentiation.
Exponentiation where the exponent is a matrix
is used for solving systems of linear differential equation
s.
Exponentiation is used pervasively in many other fields as well, including economics, biology, chemistry, physics, and computer science, with applications such as compound interest
, population growth
, chemical reaction kinetics, wave
behavior, and public key cryptography.
.
The expression
a3 = a·a·a is called the cube, because the volume of a cube with side-length a is a3.
So 32 is pronounced "three squared", and 23 is "two cubed".
The exponent says how many copies of the base are multiplied together. For example, 35 = 3·3·3·3·3 = 243. The base 3 appears 5 times in the repeated multiplication, because the exponent is 5.
Here, 3 is the base, 5 is the exponent, and 243 is the power or, more specifically, the fifth power of 3, 3 raised to the fifth power, or 3 to the power of 5.
The word "raised" is usually omitted, and very often "power" as well, so 35 is typically pronounced "three to the fifth" or "three to the five".
Formally, powers with positive integer exponents may be defined by the initial condition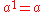
and the recurrence relation

 :
: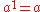

Extending these equations to zero exponents, we have
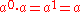
and therefore, for all nonzero

These equations do not decide the value of 00, which is discussed below.
Another way of saying this is that when n, m, and n − m are positive (and if a is not equal to zero), one can see that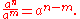
Extended to the special case when n and m are equal, the equality would read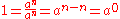
since both the numerator and the denominator are equal. Therefore we take this as the definition of a0. This leads to the following rule:


By extending these equations to negative integers (for nonzero ), we get
), we get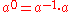
therefore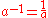
(In other words, raising a nonzero number to the −1 power produces its reciprocal
).
Similarly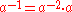
therefore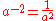
and in general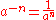
for any nonzero a and any positive integer n. Raising 0 to a negative power would imply division by 0
, so it is left undefined.
The definition of a−n for nonzero a is made so that the identity aman = am+n, initially true only for nonnegative integers m and n, holds for arbitrary integers m and n. In particular, requiring this identity for m = −n is requiring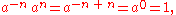
where a0 is defined above, and this motivates the definition a−n = 1/an shown above.
Exponentiation to a negative integer power can alternatively be seen as repeated division
of 1 by the base.
For instance,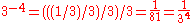 .
.
s from an n-element set, or the number of m-letter words from an n-letter alphabet.
See also exponentiation over sets.
satisfied by integer exponentiation is
This identity has the consequence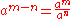
for a ≠ 0, and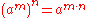
Another basic identity is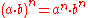
While addition and multiplication are commutative (for example,
2+3 = 5 = 3+2 and
2·3 = 6 = 3·2), exponentiation is not commutative:
23 = 8, but 32 = 9.
Similarly, while addition and multiplication are associative (for example,
(2+3)+4 = 9 = 2+(3+4) and
(2·3)·4 = 24 = 2·(3·4), exponentiation is not associative either:
23 to the 4th power is 84 or 4096, but 2 to the 34 power is
281 or 2,417,851,639,229,258,349,412,352. Without parentheses to modify the order of calculation, the order is usually understood to be top-down, not bottom-up: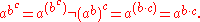
In the base ten (decimal
) number system, integer powers of 10 are written as the digit 1 followed or preceded by a number of zeroes determined by the sign and magnitude of the exponent. For example, 103 = 1000 and 10−4 = 0.0001.
Exponentiation with base 10
is used in scientific notation
to describe large or small numbers. For instance, 299,792,458 meters/second
(the speed of light
in a vacuum, in meters per second) can be written as 2.99792458·108 m/s and then approximated
as 2.998·108 m/s.
SI prefix
es based on powers of 10 are also used to describe small or large quantities. For example, the prefix kilo means 103 = 1000, so a kilometre is 1000 metres.
are important in computer science
because there are 2n possible values for an n-bit
binary
variable
.
Powers of 2 are important in set theory
since a set with n members has a power set, or set of all subset
s of the original set, with 2n members.
The negative powers of 2 are commonly used, and the first two have special names: half, and quarter.
In the base 2 (binary) number system, integer powers of 2 are written as 1 followed or preceded by a number of zeroes determined by the sign and magnitude of the exponent. For example, two to the power of three is written 1000 in binary.
If the exponent is negative, the power of zero (0n, where n < 0) is undefined, because division by zero is implied.
If the exponent is zero, some authors define 00=1, whereas others leave it undefined, as discussed below.
If n is an odd integer, then (−1)n = −1.
Because of this, powers of −1 are useful for expressing alternating sequences. For a similar discussion of powers of the complex number i, see the section on Powers of complex numbers.
of powers of a number greater than one diverges, in other words they grow without bound:
This can be read as "a to the power of n tends to +∞
as n tends to infinity when a is greater than one".
Powers of a number with absolute value
less than one tend to zero:
Any power of one is always itself:
If the number a varies tending to 1 as the exponent tends to infinity then the limit is not necessarily one of those above. A particularly important case isn → e as n→∞
see the section below Powers of e.
Other limits, in particular of those tending to indeterminate forms, are described in limits of powers below.

By extending this equation to cases where or
or  are rational number
are rational number
s, we may define exponentiation on such numbers. For example: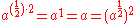
therefore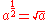
More generally, where is positive:
is positive:
The identities and properties shown above for integer exponents are true for positive real numbers with noninteger exponents as well. However the identity
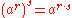
cannot be extended consistently to where a is a negative real number, see negative nth roots. The failure of this identity is the basis for the problems with complex number powers detailed under failure of power and logarithm identities.
a is a number x such that xn = a.
If a is a positive real number and n is a positive integer, then there is exactly one positive real solution to xn = a.
This solution is called the principal n-th root
of a.
It is denoted n√a,
where √ is the radical symbol
; alternatively, it may be written a1/n.
For example: 41/2 = 2, 81/3 = 2,
When one speaks of the n-th root of a positive real number
a, one usually means the principal n-th root.
exponent m/n in lowest terms satisfies
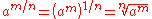
where m is an integer and n is a positive integer.
, sometimes called Euler's number, is approximately equal to 2.718 and is the base of the natural logarithm
. It provides a path for defining exponentiation with noninteger exponents. It is defined as the following limit where the power goes to infinity as the base tends to one:
The exponential function
, defined by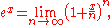
has the x written as a power as it satisfies the basic exponential identity
The exponential function is defined for all integer, fractional, real, and complex
values of x. It can even be used to extend exponentiation to some nonnumerical entities such as square matrices; however, the exponential identity only holds when x and y commute.
A short proof that e to a positive integer power k is the same as ek is: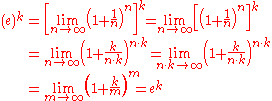
This proof shows also that ex+y satisfies the exponential identity when x and y are positive integers. These results are in fact generally true for all numbers, not just for the positive integers.
can be approximated by rational numbers, exponentiation to an arbitrary real exponent x can be defined by continuity
with the rule

where the limit as r gets close to x is taken only over rational values of r.
For example, if
then
Exponentiation by a real power is normally accomplished using logarithms instead of using limits of rational powers.
The natural logarithm
ln(x) is the inverse
of the exponential function ex. It is defined for b > 0, and satisfies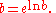
If bx is to preserve the logarithm and exponent rules,
then one must have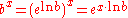
for each real number x.
This can be used as an alternative definition of the real number power bx and agrees with the definition given above using rational exponents and continuity. The definition of exponentiation using logarithms is more common in the context of complex numbers, as discussed below.
If n is even, then xn = a has two real solutions if a is positive, which are the positive and negative nth roots. The equation has no solution in real numbers if a is negative.
If n is odd, then xn = a has one real solution. The solution is positive if a is positive and negative if a is negative.
Rational powers m/n, where m/n is in lowest terms, are positive if m is even, negative for negative a if m and n are odd, and can be either sign if a is positive and n is even. (−27)1/3 = −3, (−27)2/3 = 9, and 43/2 has two roots 8 and −8. Since there is no real number x such that x2 = −1, the definition of am/n when a is negative and n is even must use the imaginary unit
i, as described more fully in the section Powers of complex numbers.
Neither the logarithm method nor the rational exponent method can be used to define ar as a real number for a negative real number a and an arbitrary real number r. Indeed, er is positive for every real number r, so ln(a) is not defined as a real number for a ≤ 0. (On the other hand, arbitrary complex powers of negative numbers a can be defined by choosing a complex logarithm
of a.)
The rational exponent method cannot be used for negative values of a because it relies on continuity
. The function f(r) = ar has a unique continuous extension from the rational numbers to the real numbers for each a > 0. But when a < 0, the function f is not even continuous on the set of rational numbers r for which it is defined.
For example, consider a = −1. The nth root of −1 is −1 for every odd natural number n. So if n is an odd positive integer, (−1)(m/n) = −1 if m is odd, and (−1)(m/n) = 1 if m is even. Thus the set of rational numbers q for which (−1)q = 1 is dense
in the rational numbers, as is the set of q for which (−1)q = −1. This means that the function (−1)q is not continuous at any rational number q where it is defined.
Care needs to be taken when applying the power law identities with negative nth roots. For instance,
−27 = (−27)((2/3)⋅(3/2)) = ((−27)2/3)3/2 = 93/2 = 27 is clearly wrong. The problem here occurs in taking the positive square root rather than the negative one at the last step, but in general the same sorts of problems occur as described for complex numbers in the section Failure of power and logarithm identities.
 The geometric interpretation of the operations on complex numbers and the definition of powers of e is the clue to understanding eix for real x. Consider the right triangle
The geometric interpretation of the operations on complex numbers and the definition of powers of e is the clue to understanding eix for real x. Consider the right triangle
For big values of n the triangle is almost a circular sector
with a small central angle equal to x/n radian
s. The triangles are mutually similar for all values of k. So for large values of n the limiting point of is the point on the unit circle
whose angle from the positive real axis is x radians. The polar coordinates of this point are and the cartesian coordinates are (cos x, sin x). So and this is Euler's formula
, connecting algebra
to trigonometry
by means of complex number
s.
The solutions to the equation ez = 1 are the integer multiples of 2πi: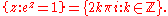
More generally, if eb = a, then every solution to ez = a can be obtained by adding an integer multiple of 2πi to b:
Thus the complex exponential function is a periodic function
with period 2πi.
More simply: eiπ = −1; ex + iy = ex(cos y + i sin y).
that the trigonometric functions cosine and sine are

Historically, cosine and sine were defined geometrically before the invention of complex numbers. The above formula reduces the complicated formulas for trigonometric functions of a sum into the simple exponentiation formula
Using exponentiation with complex exponents may reduce problems in trigonometry to algebra.
of z and the complex factor ei·y identifies the direction
of z.
For example:
and n is an integer,
then in equals 1, i, −1, or −i, according to whether the integer n is congruent to 0, 1, 2, or 3 modulo 4. Because of this, the powers of i are useful for expressing sequence
s of period 4.
Complex powers of positive reals are defined via ex as in section Complex powers of positive real numbers
above. These are continuous functions.
Trying to extend these functions to the general case of noninteger powers of complex numbers that are not positive reals leads to difficulties. Either we define discontinuous functions or multivalued function
s. Neither of these options is entirely satisfactory.
The rational power of a complex number must be the solution to an algebraic equation. Therefore it always has a finite number of possible values. For example, w = z1/2 must be a solution to the equation w2 = z. But if w is a solution, then so is −w, because (−1)2 = 1 . A unique but somewhat arbitrary solution called the principal value
can be chosen using a general rule which also applies for nonrational powers.
Complex powers and logarithms are more naturally handled as single valued functions on a Riemann surface
. Single valued versions are defined by choosing a sheet. The value has a discontinuity along a branch cut. Choosing one out of many solutions as the principal value leaves us with functions that are not continuous, and the usual rules for manipulating powers can lead us astray.
Any nonrational power of a complex number has an infinite number of possible values because of the multi-valued nature of the complex logarithm
(see below). The principal value is a single value chosen from these by a rule which, amongst its other properties, ensures powers of complex numbers with a positive real part and zero imaginary part give the same value as for the corresponding real numbers.
Exponentiating a real number to a complex power is formally a different operation from that for the corresponding complex number. However in the common case of a positive real number the principal value is the same.
The powers of negative real numbers are not always defined and are discontinuous even where defined. When dealing with complex numbers the complex number operation is normally used instead.
is.
To obtain a value of ab, first choose a logarithm of a; call it log a. Such a choice may be the principal value Log a (the default, if no other specification is given), or perhaps a value given by some other branch of log z fixed in advance. Then, using the complex exponential function one defines

because this agrees with the earlier definition in the case where a is a positive real number and the (real) principal value of log a is used.
If b is an integer
, then the value of ab is independent of the choice of log a, and it agrees with the earlier definition of exponentation with an integer exponent.
If b is a rational number
m/n in lowest terms with n > 0, then the infinitely many choices of log a yield only n different values for ab; these values are the n complex solutions z to the equation zn = am.
If b is an irrational number
, then the infinitely many choices of log a lead to infinitely many distinct values for ab.
The computation of complex powers is facilitated by converting the base a to polar form, as described in detail below.
A similar construction is employed in quaternions.
If zn = 1 but zk ≠ 1 for all natural numbers k such that 0 < k < n, then z is called a primitive nth root of unity. The negative unit −1 is the only primitive square root of unity. The imaginary unit
i is one of the two primitive 4-th roots of unity; the other one is −i.
The number e2πi (1/n) is the primitive nth root of unity with the smallest positive complex argument. (It is sometimes called the principal nth root of unity, although this terminology is not universal and should not be confused with the principal value
of n√1, which is 1.)
The other nth roots of unity are given by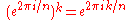
for 2 ≤ k ≤ n.
It is conventional in mathematics to define a1/n as the principal value of the root. If a is a positive real number, it is also conventional to select a positive real number as the principal value of the root a1/n. For general complex numbers, the nth root with the smallest argument is often selected as the principal value of the nth root operation, as with principal values of roots of unity.
The set of nth roots of a complex number a is obtained by multiplying the principal value a1/n by each of the nth roots of unity. For example, the fourth roots of 16 are 2, −2, 2i, and −2i, because the principal value of the fourth root of 16 is 2 and the fourth roots of unity are 1, −1, i, and −i.
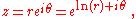
where r is a nonnegative real number and θ is the (real) argument of z. The polar form has a simple geometric interpretation: if a complex number u + iv is thought of as representing a point (u, v) in the complex plane
using Cartesian coordinates
, then (r, θ) is the same point in polar coordinates. That is, r is the "radius" r2 = u2 + v2 and θ is the "angle" θ = atan2
(v, u). The polar angle θ is ambiguous since any multiple of 2π could be added to θ without changing the location of the point. Each choice of θ gives in general a different possible value of the power. A branch cut can be used to choose a specific value. The principal value (the most common branch cut), corresponds to θ chosen in the interval (−π, π]. For complex numbers with a positive real part and zero imaginary part using the principal value gives the same result as using the corresponding real number.
In order to compute the complex power ab, write a in polar form: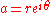 .
.
Then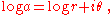
and thus
If b is decomposed as c + di, then the formula for ab can be written more explicitly as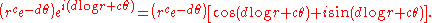
This final formula allows complex powers to be computed easily from decompositions of the base into polar form and the exponent into Cartesian form. It is shown here both in polar form and in Cartesian form (via Euler's identity).
The following examples use the principal value, the branch cut which causes θ to be in the interval (−π, π]. To compute ii, write i in polar and Cartesian forms: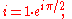

Then the formula above, with r = 1, θ = π/2, c = 0, and d = 1, yields: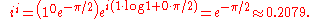
Similarly, to find (−2)3 + 4i, compute the polar form of −2,
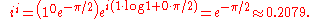
and use the formula above to compute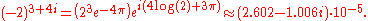
The value of a complex power depends on the branch used. For example, if the polar form i = 1ei(5π/2) is used to compute i i, the power is found to be e−5π/2; the principal value of i i, computed above, is e−π/2. The set of all possible values for i i is given by:
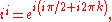
So there is an infinity of values which are possible candidates for the value of ii, one for each integer k. All of them have a zero imaginary part so one can say ii has an infinity of valid real values.
In most settings not involving continuity
in the exponent, interpreting 00 as 1 simplifies formulas and eliminates the need for special cases in theorems. (See the next paragraph for some settings that do involve continuity.)
For example:
On the other hand, when 00 arises from a limit
of the form , it must be handled as an indeterminate form
, it must be handled as an indeterminate form
.
The debate has been going on at least since the early 19th century.
At that time, most mathematicians agreed that 00 = 1, until in 1821 Cauchy listed 00 along with expressions like in a table of undefined forms.
In the 1830s Libri published an unconvincing argument for 00 = 1, and Möbius
sided with him, erroneously claiming that
 whenever
whenever 
A commentator who signed his name simply as "S" provided the counterexample of (e−1/t)t, and this quieted the debate for some time, with the apparent conclusion of this episode being that 00 should be undefined.
More details can be found in Knuth (1992).
behaviour. The Java
standard mandates this behavior. The .NET Framework
method
00. The limits in these examples exist, but have different values, showing that the two-variable function xy has no limit at the point (0,0). One may ask at what points this function does have a limit.
More precisely, consider the function f(x,y) = xy defined on D = {(x,y) ∈ R2 : x > 0}. Then D can be viewed as a subset of 2 (that is, the set of all pairs (x,y) with x,y belonging to the extended real number line
= [−∞, +∞], endowed with the product topology
), which will contain the points at which the function f has a limit.
In fact, f has a limit at all accumulation points of D, except for (0,0), (+∞,0), (1,+∞) and (1,−∞). Accordingly, this allows one to define the powers xy by continuity whenever 0 ≤ x ≤ +∞, −∞ ≤ y ≤ +∞, except for 00, (+∞)0, 1+∞ and 1−∞, which remain indeterminate forms.
Under this definition by continuity, we obtain:
These powers are obtained by taking limits of xy for positive values of x. This method does not permit a definition of xy when x < 0, since pairs (x,y) with x < 0 are not accumulation points of D.
On the other hand, when n is an integer, the power xn is already meaningful for all values of x, including negative ones. This may make the definition 0n = +∞ obtained above for negative n problematic when n is odd, since in this case tn → +∞ as t tends to 0 through positive values, but not negative ones.
This series of steps only requires 8 multiplication operations instead of 99 (since the last product above takes 2 multiplications).
In general, the number of multiplication operations required to compute
an can be reduced to Θ(log n) by using exponentiation by squaring
or (more generally) addition-chain exponentiation
. Finding the minimal sequence of multiplications (the minimal-length addition chain for the exponent) for an is a difficult problem for which no efficient algorithms are currently known (see Subset sum problem), but many reasonably efficient heuristic algorithms are available.
rather than repeated multiplication. Thus f 3(x) may mean f(f(f(x)));
in particular, f −1(x) usually denotes the inverse function
of f. Iterated function
s are of interest in the study of fractal
s and dynamical systems. Babbage was the first to study the problem of finding a functional square root
f 1/2(x).
However, for historical reasons, a special syntax applies to the trigonometric functions: a positive exponent applied to the function's abbreviation means that the result is raised to that power, while an exponent of −1 denotes the inverse function. That is, sin2x is just a shorthand way to write (sin x)2 without using parentheses, whereas sin−1x refers to the inverse function of the sine
, also called arcsin x. There is no need for a shorthand for the reciprocals of trigonometric functions since each has its own name and abbreviation; for example,
1/(sin x) = (sin x)−1 = csc x. A similar convention applies to logarithms, where log2x usually means (log x)2, not log log x.
.
Let X be a set with a power-associative binary operation
which is written multiplicatively. Then xn is defined for any element x of X and any nonzero natural number
n as the product of n copies of x, which is recursively defined by
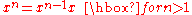
One has the following properties
If the operation has a two-sided identity element
1 (often denoted by e), then x0 is defined to be equal to 1 for any x.
If the operation also has two-sided inverses
, and multiplication is associative then the magma
is a group
. The inverse of x can be denoted by x−1 and follows all the usual rules for exponents.
If the multiplication operation is commutative (as for instance in abelian group
s), then the following holds:
If the binary operation is written additively, as it often is for abelian groups, then "exponentiation is repeated multiplication" can be reinterpreted as "multiplication
is repeated addition
". Thus, each of the laws of exponentiation above has an analogue
among laws of multiplication.
When one has several operations around, any of which might be repeated using exponentiation, it is common to indicate which operation is being repeated by placing its symbol in the superscript. Thus, x∗n is x ∗ ··· ∗ x, while x#n is x # ··· # x, whatever the operations ∗ and # might be.
Superscript notation is also used, especially in group theory
, to indicate conjugation
. That is, gh = h−1gh, where g and h are elements of some group. Although conjugation obeys some of the same laws as exponentiation, it is not an example of repeated multiplication in any sense. A quandle is an algebraic structure
in which these laws of conjugation play a central role.
For an infinite cardinal number
κ and a set A, the notation Aκ is also used to denote the set of all functions from a set of size κ to A. This is sometimes written κA to distinguish it from cardinal exponentiation, defined below.
This generalized exponential can also be defined for operations on sets or for sets with extra structure
. For example, in linear algebra
, it makes sense to index direct sum
s of vector space
s over arbitrary index sets.
That is, we can speak of
where each Vi is a vector space.
Then if Vi = V for each i, the resulting direct sum can be written in exponential notation as V⊕N, or simply VN with the understanding that the direct sum is the default.
We can again replace the set N with a cardinal number n to get Vn, although without choosing a specific standard set with cardinality n, this is defined only up to
isomorphism
.
Taking V to be the field R of real number
s (thought of as a vector space over itself) and n to be some natural number
, we get the vector space that is most commonly studied in linear algebra, the Euclidean space
Rn.
If the base of the exponentiation operation is a set, the exponentiation operation is the Cartesian product
unless otherwise stated. Since multiple Cartesian products produce an n-tuple
, which can be represented by a function on a set of appropriate cardinality, SN becomes simply the set of all function
s from N to S in this case:
This fits in with the exponentiation of cardinal numbers, in the sense that |SN| = |S||N|, where |X| is the cardinality of X.
When "2" is defined as {0,1}, we have |2X| = 2|X|, where 2X, usually denoted by P(X), is the power set of X; each subset
Y of X corresponds uniquely to a function on X taking the value 1 for x ∈ Y and 0 for x ∉ Y.
, the exponential operation can be used to raise an arbitrary object to the power of another object. This generalizes the Cartesian product
in the category of sets.
If is an initial object
is an initial object
in a Cartesian closed category, then the exponential object
 is isomorphic to any terminal object
is isomorphic to any terminal object  .
.
, there are exponential operations for cardinal
and ordinal number
s.
If κ and λ are cardinal numbers, the expression κλ represents the cardinality of the set of functions from any set of cardinality λ to any set of cardinality κ. If κ and λ are finite, then this agrees with the ordinary arithmetic exponential operation. For example, the set of 3-tuples of elements from a 2-element set has cardinality 8 = 23.
Exponentiation of cardinal numbers is distinct from exponentiation of ordinal numbers, which is defined by a limit
process involving transfinite induction
.
. Iterating tetration leads to another operation, and so on. This sequence of operations is expressed by the Ackermann function
and Knuth's up-arrow notation
. Just as exponentiation grows faster than multiplication, which is faster growing than addition, tetration is faster growing than exponentiation. Evaluated at (3,3), the functions addition, multiplication, exponentiation, tetration yield 6, 9, 27, and 7,625,597,484,987 respectively.
s and computer terminal
s that align the baselines of all characters on each line. Many programming language
s have alternate ways of expressing exponentiation that do not use superscripts:
In Bash, C, C++, C#, Java, JavaScript, Perl, PHP, Python and Ruby, the symbol ^ represents bitwise XOR. In Pascal, it represents indirection
. In OCaml and Standard ML, it represents string concatenation
.
mathematician Euclid
for the square of a line. In the 9th century, Muhammad ibn Mūsā al-Khwārizmī
used the terms mal for a square and kab for a cube, which later Islamic mathematicians represented in mathematical notation
as m and k, respectively, by the 15th century, as seen in the work of Abū al-Hasan ibn Alī al-Qalasādī
.
Nicolas Chuquet
used a form of exponential notation in the 15th century, which was later used by Henricus Grammateus
and Michael Stifel
in the 16th century. Samuel Jeake
introduced the term indices in 1696. In the 16th century Robert Recorde
used the terms square, cube, zenzizenzic (fourth power), surfolide (fifth), zenzicube (sixth), second surfolide (seventh) and Zenzizenzizenzic
(eighth). Biquadrate has been used to refer to the fourth power as well.
Some mathematicians (e.g., Isaac Newton
) used exponents only for powers greater than two, preferring to represent squares as repeated multiplication. Thus they would write polynomials, for example, as ax + bxx + cx3 + d.
Another historical synonym, involution, is now rare and should not be confused with its more common meaning.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
operation
Operation (mathematics)
The general operation as explained on this page should not be confused with the more specific operators on vector spaces. For a notion in elementary mathematics, see arithmetic operation....
, written as an, involving two numbers, the base
Radix
In mathematical numeral systems, the base or radix for the simplest case is the number of unique digits, including zero, that a positional numeral system uses to represent numbers. For example, for the decimal system the radix is ten, because it uses the ten digits from 0 through 9.In any numeral...
a and the exponent (or power) n. When n is a positive integer, exponentiation corresponds to repeated multiplication
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
; in other words, a product of n factors of a (the product itself can also be called power):
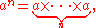
just as multiplication by a positive integer corresponds to repeated addition
Addition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
:

The exponent is usually shown as a superscript to the right of the base. The exponentiation an can be read as: a raised to the n-th power, a raised to the power [of] n, or possibly a raised to the exponent [of] n, or more briefly as a to the n. Some exponents have their own pronunciation: for example, a2 is usually read as a squared and a3 as a cubed. When superscripts cannot be used, as in plain ASCII text
ASCII
The American Standard Code for Information Interchange is a character-encoding scheme based on the ordering of the English alphabet. ASCII codes represent text in computers, communications equipment, and other devices that use text...
, common alternative formats include a^n and a**n.
The power an can be defined also when n is a negative integer, for nonzero a.
No natural extension to all real a and n exists,
but when the base a is a positive real number, an can be defined for all real and even complex exponents n via the exponential function
Exponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
ez. Trigonometric functions
Trigonometry
Trigonometry is a branch of mathematics that studies triangles and the relationships between their sides and the angles between these sides. Trigonometry defines the trigonometric functions, which describe those relationships and have applicability to cyclical phenomena, such as waves...
can be expressed in terms of complex exponentiation.
Exponentiation where the exponent is a matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
is used for solving systems of linear differential equation
Linear differential equation
Linear differential equations are of the formwhere the differential operator L is a linear operator, y is the unknown function , and the right hand side ƒ is a given function of the same nature as y...
s.
Exponentiation is used pervasively in many other fields as well, including economics, biology, chemistry, physics, and computer science, with applications such as compound interest
Compound interest
Compound interest arises when interest is added to the principal, so that from that moment on, the interest that has been added also itself earns interest. This addition of interest to the principal is called compounding...
, population growth
Population growth
Population growth is the change in a population over time, and can be quantified as the change in the number of individuals of any species in a population using "per unit time" for measurement....
, chemical reaction kinetics, wave
Wave
In physics, a wave is a disturbance that travels through space and time, accompanied by the transfer of energy.Waves travel and the wave motion transfers energy from one point to another, often with no permanent displacement of the particles of the medium—that is, with little or no associated mass...
behavior, and public key cryptography.
Terminology
When this article refers to 'an odd power' of a number it means the exponent is an odd number, not that the result is odd. For instance 23 which is 8 is an odd power of 2 because the exponent is 3. This is the usual usage and applies to any similar form like an even power, negative power, or positive power.Integer exponents
The exponentiation operation with integer exponents requires only elementary algebraElementary algebra
Elementary algebra is a fundamental and relatively basic form of algebra taught to students who are presumed to have little or no formal knowledge of mathematics beyond arithmetic. It is typically taught in secondary school under the term algebra. The major difference between algebra and...
.
Positive integer exponents
The expression a2 = a·a is called the square of a because the area of a square with side-length a is a2.The expression
a3 = a·a·a is called the cube, because the volume of a cube with side-length a is a3.
So 32 is pronounced "three squared", and 23 is "two cubed".
The exponent says how many copies of the base are multiplied together. For example, 35 = 3·3·3·3·3 = 243. The base 3 appears 5 times in the repeated multiplication, because the exponent is 5.
Here, 3 is the base, 5 is the exponent, and 243 is the power or, more specifically, the fifth power of 3, 3 raised to the fifth power, or 3 to the power of 5.
The word "raised" is usually omitted, and very often "power" as well, so 35 is typically pronounced "three to the fifth" or "three to the five".
Formally, powers with positive integer exponents may be defined by the initial condition
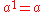
and the recurrence relation
Recurrence relation
In mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms....

Zero exponent
From the previous section, we have, for positive :
: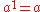

Extending these equations to zero exponents, we have
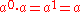
and therefore, for all nonzero


These equations do not decide the value of 00, which is discussed below.
Another way of saying this is that when n, m, and n − m are positive (and if a is not equal to zero), one can see that
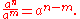
Extended to the special case when n and m are equal, the equality would read
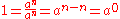
since both the numerator and the denominator are equal. Therefore we take this as the definition of a0. This leads to the following rule:
- Any number raised to the power 1 is the number itself.
- Any nonzero number raised to the power 0 is 1; one interpretation of these powers is as empty productEmpty productIn mathematics, an empty product, or nullary product, is the result of multiplying no factors. It is equal to the multiplicative identity 1, given that it exists for the multiplication operation in question, just as the empty sum—the result of adding no numbers—is zero, or the additive...
s.
Negative integer exponents
We have defined exponentiation with nonnegative integer exponents as follows:

By extending these equations to negative integers (for nonzero
 ), we get
), we get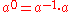
therefore
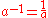
(In other words, raising a nonzero number to the −1 power produces its reciprocal
Multiplicative inverse
In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
).
Similarly
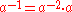
therefore
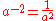
and in general
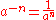
for any nonzero a and any positive integer n. Raising 0 to a negative power would imply division by 0
Division by zero
In mathematics, division by zero is division where the divisor is zero. Such a division can be formally expressed as a / 0 where a is the dividend . Whether this expression can be assigned a well-defined value depends upon the mathematical setting...
, so it is left undefined.
The definition of a−n for nonzero a is made so that the identity aman = am+n, initially true only for nonnegative integers m and n, holds for arbitrary integers m and n. In particular, requiring this identity for m = −n is requiring
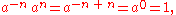
where a0 is defined above, and this motivates the definition a−n = 1/an shown above.
Exponentiation to a negative integer power can alternatively be seen as repeated division
Division (mathematics)
right|thumb|200px|20 \div 4=5In mathematics, especially in elementary arithmetic, division is an arithmetic operation.Specifically, if c times b equals a, written:c \times b = a\,...
of 1 by the base.
For instance,
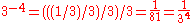 .
.Combinatorial interpretation
For nonnegative integers n and m, the power nm equals the cardinality of the set of m-tupleTuple
In mathematics and computer science, a tuple is an ordered list of elements. In set theory, an n-tuple is a sequence of n elements, where n is a positive integer. There is also one 0-tuple, an empty sequence. An n-tuple is defined inductively using the construction of an ordered pair...
s from an n-element set, or the number of m-letter words from an n-letter alphabet.
| 05 = │ {} │ = 0. | There is no 5-tuple from the empty set. |
| 14 = │ { (1,1,1,1) } │ = 1. | There is one 4-tuple from a one-element set. |
| 23 = │ { (1,1,1), (1,1,2), (1,2,1), (1,2,2), (2,1,1), (2,1,2), (2,2,1), (2,2,2) } │ = 8. | There are eight 3-tuples from a two-element set. |
| 32 = │ { (1,1), (1,2), (1,3), (2,1), (2,2), (2,3), (3,1), (3,2), (3,3) } │ = 9. | There are nine 2-tuples from a three-element set. |
| 41 = │ { (1), (2), (3), (4) } │ = 4. | There are four 1-tuples from a four-element set. |
| 50 = │ { } │ = 1. | There is exactly one empty tuple. |
See also exponentiation over sets.
Identities and properties
The most important identityIdentity (mathematics)
In mathematics, the term identity has several different important meanings:*An identity is a relation which is tautologically true. This means that whatever the number or value may be, the answer stays the same. For example, algebraically, this occurs if an equation is satisfied for all values of...
satisfied by integer exponentiation is

This identity has the consequence
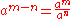
for a ≠ 0, and
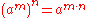
Another basic identity is
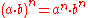
While addition and multiplication are commutative (for example,
2+3 = 5 = 3+2 and
2·3 = 6 = 3·2), exponentiation is not commutative:
23 = 8, but 32 = 9.
Similarly, while addition and multiplication are associative (for example,
(2+3)+4 = 9 = 2+(3+4) and
(2·3)·4 = 24 = 2·(3·4), exponentiation is not associative either:
23 to the 4th power is 84 or 4096, but 2 to the 34 power is
281 or 2,417,851,639,229,258,349,412,352. Without parentheses to modify the order of calculation, the order is usually understood to be top-down, not bottom-up:
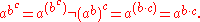
Powers of ten
- See Scientific notationScientific notationScientific notation is a way of writing numbers that are too large or too small to be conveniently written in standard decimal notation. Scientific notation has a number of useful properties and is commonly used in calculators and by scientists, mathematicians, doctors, and engineers.In scientific...
In the base ten (decimal
Decimal
The decimal numeral system has ten as its base. It is the numerical base most widely used by modern civilizations....
) number system, integer powers of 10 are written as the digit 1 followed or preceded by a number of zeroes determined by the sign and magnitude of the exponent. For example, 103 = 1000 and 10−4 = 0.0001.
Exponentiation with base 10
10 (number)
10 is an even natural number following 9 and preceding 11.-In mathematics:Ten is a composite number, its proper divisors being , and...
is used in scientific notation
Scientific notation
Scientific notation is a way of writing numbers that are too large or too small to be conveniently written in standard decimal notation. Scientific notation has a number of useful properties and is commonly used in calculators and by scientists, mathematicians, doctors, and engineers.In scientific...
to describe large or small numbers. For instance, 299,792,458 meters/second
Second
The second is a unit of measurement of time, and is the International System of Units base unit of time. It may be measured using a clock....
(the speed of light
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
in a vacuum, in meters per second) can be written as 2.99792458·108 m/s and then approximated
Approximation
An approximation is a representation of something that is not exact, but still close enough to be useful. Although approximation is most often applied to numbers, it is also frequently applied to such things as mathematical functions, shapes, and physical laws.Approximations may be used because...
as 2.998·108 m/s.
SI prefix
SI prefix
The International System of Units specifies a set of unit prefixes known as SI prefixes or metric prefixes. An SI prefix is a name that precedes a basic unit of measure to indicate a decadic multiple or fraction of the unit. Each prefix has a unique symbol that is prepended to the unit symbol...
es based on powers of 10 are also used to describe small or large quantities. For example, the prefix kilo means 103 = 1000, so a kilometre is 1000 metres.
Powers of two
The positive powers of 2Power of two
In mathematics, a power of two means a number of the form 2n where n is an integer, i.e. the result of exponentiation with as base the number two and as exponent the integer n....
are important in computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
because there are 2n possible values for an n-bit
Bit
A bit is the basic unit of information in computing and telecommunications; it is the amount of information stored by a digital device or other physical system that exists in one of two possible distinct states...
binary
Binary numeral system
The binary numeral system, or base-2 number system, represents numeric values using two symbols, 0 and 1. More specifically, the usual base-2 system is a positional notation with a radix of 2...
variable
Variable (programming)
In computer programming, a variable is a symbolic name given to some known or unknown quantity or information, for the purpose of allowing the name to be used independently of the information it represents...
.
Powers of 2 are important in set theory
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
since a set with n members has a power set, or set of all subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
s of the original set, with 2n members.
The negative powers of 2 are commonly used, and the first two have special names: half, and quarter.
In the base 2 (binary) number system, integer powers of 2 are written as 1 followed or preceded by a number of zeroes determined by the sign and magnitude of the exponent. For example, two to the power of three is written 1000 in binary.
Powers of zero
If the exponent is positive, the power of zero is zero: 0n = 0, where n > 0.If the exponent is negative, the power of zero (0n, where n < 0) is undefined, because division by zero is implied.
If the exponent is zero, some authors define 00=1, whereas others leave it undefined, as discussed below.
Powers of minus one
If n is an even integer, then (−1)n = 1.If n is an odd integer, then (−1)n = −1.
Because of this, powers of −1 are useful for expressing alternating sequences. For a similar discussion of powers of the complex number i, see the section on Powers of complex numbers.
Large exponents
The limit of a sequenceLimit of a sequence
The limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
of powers of a number greater than one diverges, in other words they grow without bound:
- an → ∞ as n → ∞ when a > 1 .
This can be read as "a to the power of n tends to +∞
Extended real number line
In mathematics, the affinely extended real number system is obtained from the real number system R by adding two elements: +∞ and −∞ . The projective extended real number system adds a single object, ∞ and makes no distinction between "positive" or "negative" infinity...
as n tends to infinity when a is greater than one".
Powers of a number with absolute value
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
less than one tend to zero:
- an → 0 as n → ∞ when |a| < 1 .
Any power of one is always itself:
- an = 1 for all n if a = 1 .
If the number a varies tending to 1 as the exponent tends to infinity then the limit is not necessarily one of those above. A particularly important case isn → e as n→∞
see the section below Powers of e.
Other limits, in particular of those tending to indeterminate forms, are described in limits of powers below.
Rational powers of positive numbers
For all integer exponents, the following relation holds:
By extending this equation to cases where
 or
or  are rational number
are rational numberRational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s, we may define exponentiation on such numbers. For example:
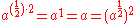
therefore
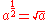
More generally, where
 is positive:
is positive:
Real powers of positive numbers
Raising a positive real number to a power that is not an integer can be accomplished in two ways.- Rational numberRational numberIn mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
exponents can be defined in terms of nth rootNth rootIn mathematics, the nth root of a number x is a number r which, when raised to the power of n, equals xr^n = x,where n is the degree of the root...
s as described above, and arbitrary nonzero exponents can then be defined by continuity. - The natural logarithmNatural logarithmThe natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
can be used to define real exponents using the exponential function.
The identities and properties shown above for integer exponents are true for positive real numbers with noninteger exponents as well. However the identity
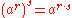
cannot be extended consistently to where a is a negative real number, see negative nth roots. The failure of this identity is the basis for the problems with complex number powers detailed under failure of power and logarithm identities.
Principal n-th root
An n-th root of a numberNumber
A number is a mathematical object used to count and measure. In mathematics, the definition of number has been extended over the years to include such numbers as zero, negative numbers, rational numbers, irrational numbers, and complex numbers....
a is a number x such that xn = a.
If a is a positive real number and n is a positive integer, then there is exactly one positive real solution to xn = a.
This solution is called the principal n-th root
Nth root
In mathematics, the nth root of a number x is a number r which, when raised to the power of n, equals xr^n = x,where n is the degree of the root...
of a.
It is denoted n√a,
where √ is the radical symbol
Symbol
A symbol is something which represents an idea, a physical entity or a process but is distinct from it. The purpose of a symbol is to communicate meaning. For example, a red octagon may be a symbol for "STOP". On a map, a picture of a tent might represent a campsite. Numerals are symbols for...
; alternatively, it may be written a1/n.
For example: 41/2 = 2, 81/3 = 2,
When one speaks of the n-th root of a positive real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
a, one usually means the principal n-th root.
Rational exponents
A power of a positive real number a with a rationalRational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
exponent m/n in lowest terms satisfies
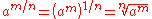
where m is an integer and n is a positive integer.
Powers of e
The important mathematical constant eE (mathematical constant)
The mathematical constant ' is the unique real number such that the value of the derivative of the function at the point is equal to 1. The function so defined is called the exponential function, and its inverse is the natural logarithm, or logarithm to base...
, sometimes called Euler's number, is approximately equal to 2.718 and is the base of the natural logarithm
Natural logarithm
The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
. It provides a path for defining exponentiation with noninteger exponents. It is defined as the following limit where the power goes to infinity as the base tends to one:

The exponential function
Exponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
, defined by
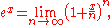
has the x written as a power as it satisfies the basic exponential identity

The exponential function is defined for all integer, fractional, real, and complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
values of x. It can even be used to extend exponentiation to some nonnumerical entities such as square matrices; however, the exponential identity only holds when x and y commute.
A short proof that e to a positive integer power k is the same as ek is:
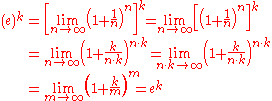
This proof shows also that ex+y satisfies the exponential identity when x and y are positive integers. These results are in fact generally true for all numbers, not just for the positive integers.
Real exponents
Since any real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
can be approximated by rational numbers, exponentiation to an arbitrary real exponent x can be defined by continuity
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
with the rule

where the limit as r gets close to x is taken only over rational values of r.
For example, if

then

Exponentiation by a real power is normally accomplished using logarithms instead of using limits of rational powers.
The natural logarithm
Natural logarithm
The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
ln(x) is the inverse
Inverse function
In mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
of the exponential function ex. It is defined for b > 0, and satisfies
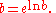
If bx is to preserve the logarithm and exponent rules,
then one must have
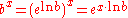
for each real number x.
This can be used as an alternative definition of the real number power bx and agrees with the definition given above using rational exponents and continuity. The definition of exponentiation using logarithms is more common in the context of complex numbers, as discussed below.
Negative nth roots
Powers of a positive real number are always positive real numbers. The solution of x2 = 4, however, can be either 2 or −2. The principal value of 41/2 is 2, but −2 is also a valid square root. If the definition of exponentiation of real numbers is extended to allow negative results then the result is no longer well behaved.If n is even, then xn = a has two real solutions if a is positive, which are the positive and negative nth roots. The equation has no solution in real numbers if a is negative.
If n is odd, then xn = a has one real solution. The solution is positive if a is positive and negative if a is negative.
Rational powers m/n, where m/n is in lowest terms, are positive if m is even, negative for negative a if m and n are odd, and can be either sign if a is positive and n is even. (−27)1/3 = −3, (−27)2/3 = 9, and 43/2 has two roots 8 and −8. Since there is no real number x such that x2 = −1, the definition of am/n when a is negative and n is even must use the imaginary unit
Imaginary unit
In mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial . The imaginary unit is denoted by , , or the Greek...
i, as described more fully in the section Powers of complex numbers.
Neither the logarithm method nor the rational exponent method can be used to define ar as a real number for a negative real number a and an arbitrary real number r. Indeed, er is positive for every real number r, so ln(a) is not defined as a real number for a ≤ 0. (On the other hand, arbitrary complex powers of negative numbers a can be defined by choosing a complex logarithm
Complex logarithm
In complex analysis, a complex logarithm function is an "inverse" of the complex exponential function, just as the natural logarithm ln x is the inverse of the real exponential function ex. Thus, a logarithm of z is a complex number w such that ew = z. The notation for such a w is log z...
of a.)
The rational exponent method cannot be used for negative values of a because it relies on continuity
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
. The function f(r) = ar has a unique continuous extension from the rational numbers to the real numbers for each a > 0. But when a < 0, the function f is not even continuous on the set of rational numbers r for which it is defined.
For example, consider a = −1. The nth root of −1 is −1 for every odd natural number n. So if n is an odd positive integer, (−1)(m/n) = −1 if m is odd, and (−1)(m/n) = 1 if m is even. Thus the set of rational numbers q for which (−1)q = 1 is dense
Dense set
In topology and related areas of mathematics, a subset A of a topological space X is called dense if any point x in X belongs to A or is a limit point of A...
in the rational numbers, as is the set of q for which (−1)q = −1. This means that the function (−1)q is not continuous at any rational number q where it is defined.
Care needs to be taken when applying the power law identities with negative nth roots. For instance,
−27 = (−27)((2/3)⋅(3/2)) = ((−27)2/3)3/2 = 93/2 = 27 is clearly wrong. The problem here occurs in taking the positive square root rather than the negative one at the last step, but in general the same sorts of problems occur as described for complex numbers in the section Failure of power and logarithm identities.
Imaginary powers of e

Right triangle
A right triangle or right-angled triangle is a triangle in which one angle is a right angle . The relation between the sides and angles of a right triangle is the basis for trigonometry.-Terminology:The side opposite the right angle is called the hypotenuse...
For big values of n the triangle is almost a circular sector
Circular sector
A circular sector or circle sector, is the portion of a disk enclosed by two radii and an arc, where the smaller area is known as the minor sector and the larger being the major sector. In the diagram, θ is the central angle in radians, r the radius of the circle, and L is the arc length of the...
with a small central angle equal to x/n radian
Radian
Radian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit...
s. The triangles are mutually similar for all values of k. So for large values of n the limiting point of is the point on the unit circle
Unit circle
In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
whose angle from the positive real axis is x radians. The polar coordinates of this point are and the cartesian coordinates are (cos x, sin x). So and this is Euler's formula
Euler's formula
Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the deep relationship between the trigonometric functions and the complex exponential function...
, connecting algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
to trigonometry
Trigonometry
Trigonometry is a branch of mathematics that studies triangles and the relationships between their sides and the angles between these sides. Trigonometry defines the trigonometric functions, which describe those relationships and have applicability to cyclical phenomena, such as waves...
by means of complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s.
The solutions to the equation ez = 1 are the integer multiples of 2πi:
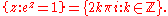
More generally, if eb = a, then every solution to ez = a can be obtained by adding an integer multiple of 2πi to b:

Thus the complex exponential function is a periodic function
Periodic function
In mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...
with period 2πi.
More simply: eiπ = −1; ex + iy = ex(cos y + i sin y).
Trigonometric functions
It follows from Euler's formulaEuler's formula
Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the deep relationship between the trigonometric functions and the complex exponential function...
that the trigonometric functions cosine and sine are

Historically, cosine and sine were defined geometrically before the invention of complex numbers. The above formula reduces the complicated formulas for trigonometric functions of a sum into the simple exponentiation formula

Using exponentiation with complex exponents may reduce problems in trigonometry to algebra.
Complex powers of e
The power z = ex+i·y can be computed as ex · ei·y. The real factor ex is the absolute valueAbsolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
of z and the complex factor ei·y identifies the direction
Direction (geometry, geography)
Direction is the information contained in the relative position of one point with respect to another point without the distance information. Directions may be either relative to some indicated reference , or absolute according to some previously agreed upon frame of reference Direction is the...
of z.
Complex powers of positive real numbers
If a is a positive real number, and z is any complex number, the power az is defined as ez·ln(a), where x = ln(a) is the unique real solution to the equation ex = a. So the same method working for real exponents also works for complex exponents.For example:
- 2i = e i·ln(2) = cos(ln(2)) + i·sin(ln(2)) ≈ 0.76924 + 0.63896i
- ei ≈ 0.54030 + 0.84147i
- 10i ≈ −0.66820 + 0.74398ii ≈ 535.49i ≈ 1
Powers of complex numbers
Integer powers of nonzero complex numbers are defined by repeated multiplication or division as above. If i is the imaginary unitImaginary unit
In mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial . The imaginary unit is denoted by , , or the Greek...
and n is an integer,
then in equals 1, i, −1, or −i, according to whether the integer n is congruent to 0, 1, 2, or 3 modulo 4. Because of this, the powers of i are useful for expressing sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
s of period 4.
Complex powers of positive reals are defined via ex as in section Complex powers of positive real numbers
above. These are continuous functions.
Trying to extend these functions to the general case of noninteger powers of complex numbers that are not positive reals leads to difficulties. Either we define discontinuous functions or multivalued function
Multivalued function
In mathematics, a multivalued function is a left-total relation; i.e. every input is associated with one or more outputs...
s. Neither of these options is entirely satisfactory.
The rational power of a complex number must be the solution to an algebraic equation. Therefore it always has a finite number of possible values. For example, w = z1/2 must be a solution to the equation w2 = z. But if w is a solution, then so is −w, because (−1)2 = 1 . A unique but somewhat arbitrary solution called the principal value
Principal value
In considering complex multiple-valued functions in complex analysis, the principal values of a function are the values along one chosen branch of that function, so it is single-valued.-Motivation:...
can be chosen using a general rule which also applies for nonrational powers.
Complex powers and logarithms are more naturally handled as single valued functions on a Riemann surface
Riemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
. Single valued versions are defined by choosing a sheet. The value has a discontinuity along a branch cut. Choosing one out of many solutions as the principal value leaves us with functions that are not continuous, and the usual rules for manipulating powers can lead us astray.
Any nonrational power of a complex number has an infinite number of possible values because of the multi-valued nature of the complex logarithm
Complex logarithm
In complex analysis, a complex logarithm function is an "inverse" of the complex exponential function, just as the natural logarithm ln x is the inverse of the real exponential function ex. Thus, a logarithm of z is a complex number w such that ew = z. The notation for such a w is log z...
(see below). The principal value is a single value chosen from these by a rule which, amongst its other properties, ensures powers of complex numbers with a positive real part and zero imaginary part give the same value as for the corresponding real numbers.
Exponentiating a real number to a complex power is formally a different operation from that for the corresponding complex number. However in the common case of a positive real number the principal value is the same.
The powers of negative real numbers are not always defined and are discontinuous even where defined. When dealing with complex numbers the complex number operation is normally used instead.
Complex power of a complex number
For complex numbers a and b with a ≠ 0, the notation ab is ambiguous in the same sense that log aComplex logarithm
In complex analysis, a complex logarithm function is an "inverse" of the complex exponential function, just as the natural logarithm ln x is the inverse of the real exponential function ex. Thus, a logarithm of z is a complex number w such that ew = z. The notation for such a w is log z...
is.
To obtain a value of ab, first choose a logarithm of a; call it log a. Such a choice may be the principal value Log a (the default, if no other specification is given), or perhaps a value given by some other branch of log z fixed in advance. Then, using the complex exponential function one defines

because this agrees with the earlier definition in the case where a is a positive real number and the (real) principal value of log a is used.
If b is an integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
, then the value of ab is independent of the choice of log a, and it agrees with the earlier definition of exponentation with an integer exponent.
If b is a rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
m/n in lowest terms with n > 0, then the infinitely many choices of log a yield only n different values for ab; these values are the n complex solutions z to the equation zn = am.
If b is an irrational number
Irrational number
In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
, then the infinitely many choices of log a lead to infinitely many distinct values for ab.
The computation of complex powers is facilitated by converting the base a to polar form, as described in detail below.
A similar construction is employed in quaternions.
Complex roots of unity
A complex number a such that an = 1 for a positive integer n is an nth root of unity. Geometrically, the nth roots of unity lie on the unit circle of the complex plane at the vertices of a regular n-gon with one vertex on the real number 1.If zn = 1 but zk ≠ 1 for all natural numbers k such that 0 < k < n, then z is called a primitive nth root of unity. The negative unit −1 is the only primitive square root of unity. The imaginary unit
Imaginary unit
In mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial . The imaginary unit is denoted by , , or the Greek...
i is one of the two primitive 4-th roots of unity; the other one is −i.
The number e2πi (1/n) is the primitive nth root of unity with the smallest positive complex argument. (It is sometimes called the principal nth root of unity, although this terminology is not universal and should not be confused with the principal value
Principal value
In considering complex multiple-valued functions in complex analysis, the principal values of a function are the values along one chosen branch of that function, so it is single-valued.-Motivation:...
of n√1, which is 1.)
The other nth roots of unity are given by
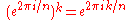
for 2 ≤ k ≤ n.
Roots of arbitrary complex numbers
Although there are infinitely many possible values for a general complex logarithm, there are only a finite number of values for the power az in the important special case where z = 1/n and n is a positive integer. These are the nth roots of a; they are solutions of the equation xn = a. As with real roots, a second root is also called a square root and a third root is also called a cube root.It is conventional in mathematics to define a1/n as the principal value of the root. If a is a positive real number, it is also conventional to select a positive real number as the principal value of the root a1/n. For general complex numbers, the nth root with the smallest argument is often selected as the principal value of the nth root operation, as with principal values of roots of unity.
The set of nth roots of a complex number a is obtained by multiplying the principal value a1/n by each of the nth roots of unity. For example, the fourth roots of 16 are 2, −2, 2i, and −2i, because the principal value of the fourth root of 16 is 2 and the fourth roots of unity are 1, −1, i, and −i.
Computing complex powers
It is often easier to compute complex powers by writing the number to be exponentiated in polar form. Every complex number z can be written in the polar form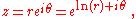
where r is a nonnegative real number and θ is the (real) argument of z. The polar form has a simple geometric interpretation: if a complex number u + iv is thought of as representing a point (u, v) in the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
using Cartesian coordinates
Cartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
, then (r, θ) is the same point in polar coordinates. That is, r is the "radius" r2 = u2 + v2 and θ is the "angle" θ = atan2
Atan2
In trigonometry, the two-argument function atan2 is a variation of the arctangent function. For any real arguments and not both equal to zero, is the angle in radians between the positive -axis of a plane and the point given by the coordinates on it...
(v, u). The polar angle θ is ambiguous since any multiple of 2π could be added to θ without changing the location of the point. Each choice of θ gives in general a different possible value of the power. A branch cut can be used to choose a specific value. The principal value (the most common branch cut), corresponds to θ chosen in the interval (−π, π]. For complex numbers with a positive real part and zero imaginary part using the principal value gives the same result as using the corresponding real number.
In order to compute the complex power ab, write a in polar form:
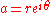 .
.Then
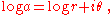
and thus

If b is decomposed as c + di, then the formula for ab can be written more explicitly as
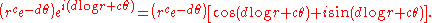
This final formula allows complex powers to be computed easily from decompositions of the base into polar form and the exponent into Cartesian form. It is shown here both in polar form and in Cartesian form (via Euler's identity).
The following examples use the principal value, the branch cut which causes θ to be in the interval (−π, π]. To compute ii, write i in polar and Cartesian forms:
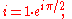

Then the formula above, with r = 1, θ = π/2, c = 0, and d = 1, yields:
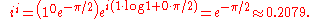
Similarly, to find (−2)3 + 4i, compute the polar form of −2,
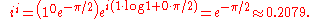
and use the formula above to compute
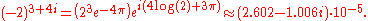
The value of a complex power depends on the branch used. For example, if the polar form i = 1ei(5π/2) is used to compute i i, the power is found to be e−5π/2; the principal value of i i, computed above, is e−π/2. The set of all possible values for i i is given by:

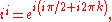
So there is an infinity of values which are possible candidates for the value of ii, one for each integer k. All of them have a zero imaginary part so one can say ii has an infinity of valid real values.
Failure of power and logarithm identities
Some identities for powers and logarithms for positive real numbers will fail for complex numbers, no matter how complex powers and complex logarithms are defined as single-valued functions. For example:- The identity log(ab) = b · log a holds whenever a is a positive real number and b is a real number. But for the principal branchPrincipal branchIn mathematics, a principal branch is a function which selects one branch, or "slice", of a multi-valued function. Most often, this applies to functions defined on the complex plane: see branch cut....
of the complex logarithm one has-
-
- Regardless of which branch of the logarithm is used, a similar failure of the identity will exist. The best that can be said (if only using this result) is that:
-
- This identity does not hold even when considering log as a multivalued function. The possible values of log(ab) contain those of b · log a as a subset. Using Log(a) for the principal value of log(a) and m, n as any integers the possible values of both sides are:
-
-
- The identities (ab)c = acbc and (a/b)c = ac/bc are valid when a and b are positive real numbers and c is a real number. But a calculation using principal branches shows that
-
-
- and
- On the other hand, when c is an integer, the identities are valid for all nonzero complex numbers.
- If exponentiation is considered as a multivalued function then the possible values of (−1×−1)1/2 are {1, −1}. The identity holds but saying {1} = {(−1×−1)1/2} is wrong.
-
- The identity (ea)b = eab holds for real numbers a and b, but assuming its truth for complex numbers leads to the following paradox, discovered in 1827 by ClausenThomas Clausen (mathematician)Thomas Clausen was a Danish mathematician and astronomer....
:- For any integer n, we have:
-
- but this is false when the integer n is nonzero.
- There are a number of problems in the reasoning:
- The major error is that changing the order of exponentiation in going from line two to three changes what the principal value chosen will be.
- From the multi-valued point of view the first error occurs even sooner, it is implicit in the first line and not obvious. It is that e is a real number whereas the result of e1+2πin is a complex number better represented as e+0i. Substituting the complex number for the real on the second line makes the power have multiple possible values. Changing the order of exponentiation from lines two to three also affects how many possible values the result can have.
- For any integer n, we have:
Zero to the zero power
Most authors agree with the statements related to 00 in the two lists below, but make different decisions when it comes to defining 00 or not: see the next subsection.In most settings not involving continuity
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
in the exponent, interpreting 00 as 1 simplifies formulas and eliminates the need for special cases in theorems. (See the next paragraph for some settings that do involve continuity.)
For example:
- Regarding a0 as an empty productEmpty productIn mathematics, an empty product, or nullary product, is the result of multiplying no factors. It is equal to the multiplicative identity 1, given that it exists for the multiplication operation in question, just as the empty sum—the result of adding no numbers—is zero, or the additive...
assigns it the value 1, even when a = 0. - The combinatorial interpretation of 00 is the number of empty tuples of elements from the empty set. There is exactly one empty tuple.
- Equivalently, the set-theoretic interpretation of 00 is the number of functions from the empty set to the empty set. There is exactly one such function, the empty functionEmpty functionIn mathematics, an empty function is a function whose domain is the empty set. For each set A, there is exactly one such empty functionf_A: \varnothing \rightarrow A....
. - The notation
 for polynomialPolynomialIn mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
for polynomialPolynomialIn mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s and power series rely on defining 00 = 1. Identities like and
and  and the binomial theoremBinomial theoremIn elementary algebra, the binomial theorem describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the power n into a sum involving terms of the form axbyc, where the exponents b and c are nonnegative integers with , and the coefficient a of...
and the binomial theoremBinomial theoremIn elementary algebra, the binomial theorem describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the power n into a sum involving terms of the form axbyc, where the exponents b and c are nonnegative integers with , and the coefficient a of...
 are not valid for x = 0 unless 00 = 1.
are not valid for x = 0 unless 00 = 1. - In differential calculusDifferential calculusIn mathematics, differential calculus is a subfield of calculus concerned with the study of the rates at which quantities change. It is one of the two traditional divisions of calculus, the other being integral calculus....
, the power rule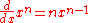 is not valid for n = 1 at x = 0 unless 00 = 1.
is not valid for n = 1 at x = 0 unless 00 = 1.
On the other hand, when 00 arises from a limit
Limit of a function
In mathematics, the limit of a function is a fundamental concept in calculus and analysis concerning the behavior of that function near a particular input....
of the form
 , it must be handled as an indeterminate form
, it must be handled as an indeterminate formIndeterminate form
In calculus and other branches of mathematical analysis, an indeterminate form is an algebraic expression obtained in the context of limits. Limits involving algebraic operations are often performed by replacing subexpressions by their limits; if the expression obtained after this substitution...
.
- Limits involving algebraic operations can often be evaluated by replacing subexpressions by their limits; if the resulting expression does not determine the original limit, the expression is known as an indeterminate form. In fact, when f(t) and g(t) are real-valued functions both approaching 0 (as t approaches a real number or ±∞), with f(t) > 0, the function f(t)g(t) need not approach 1; depending on f and g, the limit of f(t)g(t) can be any nonnegative real number or +∞, or it can be undefined. For example, the functions below are of the form f(t)g(t) with f(t),g(t) → 0 as t → 0+One-sided limitIn calculus, a one-sided limit is either of the two limits of a function f of a real variable x as x approaches a specified point either from below or from above...
, but the limits are different:
-
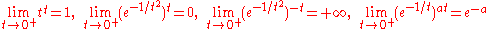 .
.
- So 00 is an indeterminate form. This behavior shows that the two-variable function xy, though continuous on the set {(x,y): x > 0}, cannot be extended to a continuous functionContinuous functionIn mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
on any set containing (0,0), no matter how 00 is defined. However, under certain conditions, such as when f and g are both analytic functions and f is nonnegative, the limit approaching from the right is always 1.- In the complex domain, the function zw is defined for nonzero z by choosing a branch of log z and setting zw := ew log z, but there is no branch of log z defined at z = 0, let alone in a neighborhood of 0.
History of differing points of view
Different authors interpret the situation above in different ways:- Some argue that the best value for 00 depends on context, and hence that defining it once and for all is problematic. According to Benson (1999), "The choice whether to define 00 is based on convenience, not on correctness."
- Others argue that 00 is 1. According to p. 408 of KnuthDonald KnuthDonald Ervin Knuth is a computer scientist and Professor Emeritus at Stanford University.He is the author of the seminal multi-volume work The Art of Computer Programming. Knuth has been called the "father" of the analysis of algorithms...
(1992), it "has to be 1", although he goes on to say that "Cauchy had good reason to consider 00 as an undefined limiting form" and that "in this much stronger sense, the value of 00 is less defined than, say, the value of 0 + 0" (emphases in original).
The debate has been going on at least since the early 19th century.
At that time, most mathematicians agreed that 00 = 1, until in 1821 Cauchy listed 00 along with expressions like in a table of undefined forms.
In the 1830s Libri published an unconvincing argument for 00 = 1, and Möbius
August Ferdinand Möbius
August Ferdinand Möbius was a German mathematician and theoretical astronomer.He is best known for his discovery of the Möbius strip, a non-orientable two-dimensional surface with only one side when embedded in three-dimensional Euclidean space. It was independently discovered by Johann Benedict...
sided with him, erroneously claiming that
 whenever
whenever 
A commentator who signed his name simply as "S" provided the counterexample of (e−1/t)t, and this quieted the debate for some time, with the apparent conclusion of this episode being that 00 should be undefined.
More details can be found in Knuth (1992).
IEEE floating point standard
The IEEE 754-2008 floating point standard is used in the design of most floating point libraries. It recommends a number of different functions for computing a power:- pow treats 00 as 1. This is the oldest defined version. If the power is an exact integer the result is the same as for pown, otherwise the result is as for powr (except for some exceptional cases).
- pown treats 00 as 1. The power must be an exact integer. The value is defined for negative bases, e.g. pown(−3,5) is −243.
- powr treats 00 as NaNNaNIn computing, NaN is a value of the numeric data type representing an undefined or unrepresentable value, especially in floating-point calculations...
(Not-a-Number – undefined). The value is also NaN for cases like powr(−3,2) where the base is less than zero. The value is defined by epower'×log(base).
Programming languages
Most programming language with a power function are implemented using the IEEE pow function and therefore evaluate 00 as 1. The later C and C++ standards describe this as the normativeNormative
Normative has specialized contextual meanings in several academic disciplines. Generically, it means relating to an ideal standard or model. In practice, it has strong connotations of relating to a typical standard or model ....
behaviour. The Java
Java (programming language)
Java is a programming language originally developed by James Gosling at Sun Microsystems and released in 1995 as a core component of Sun Microsystems' Java platform. The language derives much of its syntax from C and C++ but has a simpler object model and fewer low-level facilities...
standard mandates this behavior. The .NET Framework
.NET Framework
The .NET Framework is a software framework that runs primarily on Microsoft Windows. It includes a large library and supports several programming languages which allows language interoperability...
method
Method (computer science)
In object-oriented programming, a method is a subroutine associated with a class. Methods define the behavior to be exhibited by instances of the associated class at program run time...
System.Math.Pow also treats 00 as 1.Mathematics software
- Sage simplifies a0 to 1, even if no constraints are placed on a. It does not simplify 0a, and it takes 00 to be 1.
- MapleMaple (software)Maple is a general-purpose commercial computer algebra system. It was first developed in 1980 by the Symbolic Computation Group at the University of Waterloo in Waterloo, Ontario, Canada....
simplifies a0 to 1 and 0a to 0, even if no constraints are placed on a (the latter simplification is only valid for a > 0), and evaluates 00 to 1. - MacsymaMacsymaMacsyma is a computer algebra system that was originally developed from 1968 to 1982 at MIT as part of Project MAC and later marketed commercially...
also simplifies a0 to 1 and 0a to 0, even if no constraints are placed on a, but issues an error for 00. - MathematicaMathematicaMathematica is a computational software program used in scientific, engineering, and mathematical fields and other areas of technical computing...
and Wolfram AlphaWolfram AlphaWolfram Alpha is an answer-engine developed by Wolfram Research. It is an online service that answers factual queries directly by computing the answer from structured data, rather than providing a list of documents or web pages that might contain the answer as a search engine might...
simplify a0 into 1, even if no constraints are placed on a. While Mathematica does not simplify 0a, Wolfram Alpha returns two results, 0 and indeterminate. Both Mathematica and Wolfram Alpha take 00 to be an indeterminate formIndeterminate formIn calculus and other branches of mathematical analysis, an indeterminate form is an algebraic expression obtained in the context of limits. Limits involving algebraic operations are often performed by replacing subexpressions by their limits; if the expression obtained after this substitution...
.
Limits of powers
The section zero to the zero power gives a number of examples of limits which are of the indeterminate formIndeterminate form
In calculus and other branches of mathematical analysis, an indeterminate form is an algebraic expression obtained in the context of limits. Limits involving algebraic operations are often performed by replacing subexpressions by their limits; if the expression obtained after this substitution...
00. The limits in these examples exist, but have different values, showing that the two-variable function xy has no limit at the point (0,0). One may ask at what points this function does have a limit.
More precisely, consider the function f(x,y) = xy defined on D = {(x,y) ∈ R2 : x > 0}. Then D can be viewed as a subset of 2 (that is, the set of all pairs (x,y) with x,y belonging to the extended real number line
Extended real number line
In mathematics, the affinely extended real number system is obtained from the real number system R by adding two elements: +∞ and −∞ . The projective extended real number system adds a single object, ∞ and makes no distinction between "positive" or "negative" infinity...
= [−∞, +∞], endowed with the product topology
Product topology
In topology and related areas of mathematics, a product space is the cartesian product of a family of topological spaces equipped with a natural topology called the product topology...
), which will contain the points at which the function f has a limit.
In fact, f has a limit at all accumulation points of D, except for (0,0), (+∞,0), (1,+∞) and (1,−∞). Accordingly, this allows one to define the powers xy by continuity whenever 0 ≤ x ≤ +∞, −∞ ≤ y ≤ +∞, except for 00, (+∞)0, 1+∞ and 1−∞, which remain indeterminate forms.
Under this definition by continuity, we obtain:
- a+∞ = +∞ and a−∞ = 0, when 1 < a ≤ +∞.
- a+∞ = 0 and a−∞ = +∞, when 0 ≤ a < 1.
- 0b = 0 and (+∞)b = +∞, when 0 < b ≤ +∞.
- 0b = +∞ and (+∞)b = 0, when −∞ ≤ b < 0.
These powers are obtained by taking limits of xy for positive values of x. This method does not permit a definition of xy when x < 0, since pairs (x,y) with x < 0 are not accumulation points of D.
On the other hand, when n is an integer, the power xn is already meaningful for all values of x, including negative ones. This may make the definition 0n = +∞ obtained above for negative n problematic when n is odd, since in this case tn → +∞ as t tends to 0 through positive values, but not negative ones.
Efficient computation of integer powers
The simplest method of computing an requires n−1 multiplication operations, but it can be computed more efficiently than that, as illustrated by the following example. To compute 2100, note that 100 = 64 + 32 + 4. Compute the following in order:- 22 = 4
- (22)2 = 24 = 16
- (24)2 = 28 = 256
- (28)2 = 216 = 65,536
- (216)2 = 232 = 4,294,967,296
- (232)2 = 264 = 18,446,744,073,709,551,616
- 264 232 24 = 2100 = 1,267,650,600,228,229,401,496,703,205,376
This series of steps only requires 8 multiplication operations instead of 99 (since the last product above takes 2 multiplications).
In general, the number of multiplication operations required to compute
an can be reduced to Θ(log n) by using exponentiation by squaring
Exponentiation by squaring
Exponentiating by squaring is a general method for fast computation of large integer powers of a number. Some variants are commonly referred to as square-and-multiply algorithms or binary exponentiation. In additive notation the appropriate term is double-and-add...
or (more generally) addition-chain exponentiation
Addition-chain exponentiation
In mathematics and computer science, optimal addition-chain exponentiation is a method of exponentiation by positive integer powers that requires a minimal number of multiplications. It works by creating a shortest addition chain that generates the desired exponent. Each exponentiation in the chain...
. Finding the minimal sequence of multiplications (the minimal-length addition chain for the exponent) for an is a difficult problem for which no efficient algorithms are currently known (see Subset sum problem), but many reasonably efficient heuristic algorithms are available.
Exponential notation for function names
Placing an integer superscript after the name or symbol of a function, as if the function were being raised to a power, commonly refers to repeated function compositionFunction composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
rather than repeated multiplication. Thus f 3(x) may mean f(f(f(x)));
in particular, f −1(x) usually denotes the inverse function
Inverse function
In mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
of f. Iterated function
Iterated function
In mathematics, an iterated function is a function which is composed with itself, possibly ad infinitum, in a process called iteration. In this process, starting from some initial value, the result of applying a given function is fed again in the function as input, and this process is repeated...
s are of interest in the study of fractal
Fractal
A fractal has been defined as "a rough or fragmented geometric shape that can be split into parts, each of which is a reduced-size copy of the whole," a property called self-similarity...
s and dynamical systems. Babbage was the first to study the problem of finding a functional square root
Functional square root
In mathematics, a half iterate is a square root of a function with respect to the operation of function composition. In other words, a functional square root of a function g is a function f satisfying f = g for all x...
f 1/2(x).
However, for historical reasons, a special syntax applies to the trigonometric functions: a positive exponent applied to the function's abbreviation means that the result is raised to that power, while an exponent of −1 denotes the inverse function. That is, sin2x is just a shorthand way to write (sin x)2 without using parentheses, whereas sin−1x refers to the inverse function of the sine
Sine
In mathematics, the sine function is a function of an angle. In a right triangle, sine gives the ratio of the length of the side opposite to an angle to the length of the hypotenuse.Sine is usually listed first amongst the trigonometric functions....
, also called arcsin x. There is no need for a shorthand for the reciprocals of trigonometric functions since each has its own name and abbreviation; for example,
1/(sin x) = (sin x)−1 = csc x. A similar convention applies to logarithms, where log2x usually means (log x)2, not log log x.
In abstract algebra
Exponentiation for integer exponents can be defined for quite general structures in abstract algebraAbstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
.
Let X be a set with a power-associative binary operation
Binary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
which is written multiplicatively. Then xn is defined for any element x of X and any nonzero natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
n as the product of n copies of x, which is recursively defined by

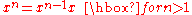
One has the following properties
-
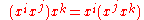 (power-associative property),
(power-associative property), -

-
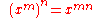
If the operation has a two-sided identity element
Identity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
1 (often denoted by e), then x0 is defined to be equal to 1 for any x.
-
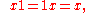 Two sided identity
Two sided identity -

If the operation also has two-sided inverses
Inverse element
In abstract algebra, the idea of an inverse element generalises the concept of a negation, in relation to addition, and a reciprocal, in relation to multiplication. The intuition is of an element that can 'undo' the effect of combination with another given element...
, and multiplication is associative then the magma
Magma (algebra)
In abstract algebra, a magma is a basic kind of algebraic structure. Specifically, a magma consists of a set M equipped with a single binary operation M \times M \rightarrow M....
is a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
. The inverse of x can be denoted by x−1 and follows all the usual rules for exponents.
-
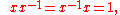 Two sided inverse
Two sided inverse -
 Associative
Associative -

-

If the multiplication operation is commutative (as for instance in abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s), then the following holds:
If the binary operation is written additively, as it often is for abelian groups, then "exponentiation is repeated multiplication" can be reinterpreted as "multiplication
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
is repeated addition
Addition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
". Thus, each of the laws of exponentiation above has an analogue
Analogy
Analogy is a cognitive process of transferring information or meaning from a particular subject to another particular subject , and a linguistic expression corresponding to such a process...
among laws of multiplication.
When one has several operations around, any of which might be repeated using exponentiation, it is common to indicate which operation is being repeated by placing its symbol in the superscript. Thus, x∗n is x ∗ ··· ∗ x, while x#n is x # ··· # x, whatever the operations ∗ and # might be.
Superscript notation is also used, especially in group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, to indicate conjugation
Conjugacy class
In mathematics, especially group theory, the elements of any group may be partitioned into conjugacy classes; members of the same conjugacy class share many properties, and study of conjugacy classes of non-abelian groups reveals many important features of their structure...
. That is, gh = h−1gh, where g and h are elements of some group. Although conjugation obeys some of the same laws as exponentiation, it is not an example of repeated multiplication in any sense. A quandle is an algebraic structure
Algebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
in which these laws of conjugation play a central role.
Over sets
If n is a natural number and A is an arbitrary set, the expression An is often used to denote the set of ordered n-tuples of elements of A. This is equivalent to letting An denote the set of functions from the set {0, 1, 2, ..., n−1} to the set A; the n-tuple (a0, a1, a2, ..., an−1) represents the function that sends i to ai.For an infinite cardinal number
Cardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
κ and a set A, the notation Aκ is also used to denote the set of all functions from a set of size κ to A. This is sometimes written κA to distinguish it from cardinal exponentiation, defined below.
This generalized exponential can also be defined for operations on sets or for sets with extra structure
Mathematical structure
In mathematics, a structure on a set, or more generally a type, consists of additional mathematical objects that in some manner attach to the set, making it easier to visualize or work with, or endowing the collection with meaning or significance....
. For example, in linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, it makes sense to index direct sum
Direct sum of modules
In abstract algebra, the direct sum is a construction which combines several modules into a new, larger module. The result of the direct summation of modules is the "smallest general" module which contains the given modules as submodules...
s of vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s over arbitrary index sets.
That is, we can speak of
where each Vi is a vector space.
Then if Vi = V for each i, the resulting direct sum can be written in exponential notation as V⊕N, or simply VN with the understanding that the direct sum is the default.
We can again replace the set N with a cardinal number n to get Vn, although without choosing a specific standard set with cardinality n, this is defined only up to
Up to
In mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
.
Taking V to be the field R of real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s (thought of as a vector space over itself) and n to be some natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
, we get the vector space that is most commonly studied in linear algebra, the Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rn.
If the base of the exponentiation operation is a set, the exponentiation operation is the Cartesian product
Cartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
unless otherwise stated. Since multiple Cartesian products produce an n-tuple
Tuple
In mathematics and computer science, a tuple is an ordered list of elements. In set theory, an n-tuple is a sequence of n elements, where n is a positive integer. There is also one 0-tuple, an empty sequence. An n-tuple is defined inductively using the construction of an ordered pair...
, which can be represented by a function on a set of appropriate cardinality, SN becomes simply the set of all function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s from N to S in this case:
This fits in with the exponentiation of cardinal numbers, in the sense that |SN| = |S||N|, where |X| is the cardinality of X.
When "2" is defined as {0,1}, we have |2X| = 2|X|, where 2X, usually denoted by P(X), is the power set of X; each subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
Y of X corresponds uniquely to a function on X taking the value 1 for x ∈ Y and 0 for x ∉ Y.
In category theory
In a Cartesian closed categoryCartesian closed category
In category theory, a category is cartesian closed if, roughly speaking, any morphism defined on a product of two objects can be naturally identified with a morphism defined on one of the factors. These categories are particularly important in mathematical logic and the theory of programming, in...
, the exponential operation can be used to raise an arbitrary object to the power of another object. This generalizes the Cartesian product
Cartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
in the category of sets.
If
 is an initial object
is an initial objectInitial object
In category theory, an abstract branch of mathematics, an initial object of a category C is an object I in C such that for every object X in C, there exists precisely one morphism I → X...
in a Cartesian closed category, then the exponential object
Exponential object
In mathematics, specifically in category theory, an exponential object is the categorical equivalent of a function space in set theory. Categories with all finite products and exponential objects are called cartesian closed categories...
 is isomorphic to any terminal object
is isomorphic to any terminal object  .
.Of cardinal and ordinal numbers
In set theorySet theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
, there are exponential operations for cardinal
Cardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
and ordinal number
Ordinal number
In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
s.
If κ and λ are cardinal numbers, the expression κλ represents the cardinality of the set of functions from any set of cardinality λ to any set of cardinality κ. If κ and λ are finite, then this agrees with the ordinary arithmetic exponential operation. For example, the set of 3-tuples of elements from a 2-element set has cardinality 8 = 23.
Exponentiation of cardinal numbers is distinct from exponentiation of ordinal numbers, which is defined by a limit
Limit (mathematics)
In mathematics, the concept of a "limit" is used to describe the value that a function or sequence "approaches" as the input or index approaches some value. The concept of limit allows mathematicians to define a new point from a Cauchy sequence of previously defined points within a complete metric...
process involving transfinite induction
Transfinite induction
Transfinite induction is an extension of mathematical induction to well-ordered sets, for instance to sets of ordinal numbers or cardinal numbers.- Transfinite induction :Let P be a property defined for all ordinals α...
.
Repeated exponentiation
Just as exponentiation of natural numbers is motivated by repeated multiplication, it is possible to define an operation based on repeated exponentiation; this operation is sometimes called tetrationTetration
In mathematics, tetration is an iterated exponential and is the next hyper operator after exponentiation. The word tetration was coined by English mathematician Reuben Louis Goodstein from tetra- and iteration. Tetration is used for the notation of very large numbers...
. Iterating tetration leads to another operation, and so on. This sequence of operations is expressed by the Ackermann function
Ackermann function
In computability theory, the Ackermann function, named after Wilhelm Ackermann, is one of the simplest and earliest-discovered examples of a total computable function that is not primitive recursive...
and Knuth's up-arrow notation
Knuth's up-arrow notation
In mathematics, Knuth's up-arrow notation is a method of notation for very large integers, introduced by Donald Knuth in 1976. It is closely related to the Ackermann function and especially to the hyperoperation sequence. The idea is based on the fact that multiplication can be viewed as iterated...
. Just as exponentiation grows faster than multiplication, which is faster growing than addition, tetration is faster growing than exponentiation. Evaluated at (3,3), the functions addition, multiplication, exponentiation, tetration yield 6, 9, 27, and 7,625,597,484,987 respectively.
In programming languages
The superscript notation xy is convenient in handwriting but inconvenient for typewriterTypewriter
A typewriter is a mechanical or electromechanical device with keys that, when pressed, cause characters to be printed on a medium, usually paper. Typically one character is printed per keypress, and the machine prints the characters by making ink impressions of type elements similar to the pieces...
s and computer terminal
Computer terminal
A computer terminal is an electronic or electromechanical hardware device that is used for entering data into, and displaying data from, a computer or a computing system...
s that align the baselines of all characters on each line. Many programming language
Programming language
A programming language is an artificial language designed to communicate instructions to a machine, particularly a computer. Programming languages can be used to create programs that control the behavior of a machine and/or to express algorithms precisely....
s have alternate ways of expressing exponentiation that do not use superscripts:
-
x ↑ y: Algol, Commodore BASICCommodore BASICCommodore BASIC, also known as PET BASIC, is the dialect of the BASIC programming language used in Commodore International's 8-bit home computer line, stretching from the PET of 1977 to the C128 of 1985... -
x ^ y: BASICBASICBASIC is a family of general-purpose, high-level programming languages whose design philosophy emphasizes ease of use - the name is an acronym from Beginner's All-purpose Symbolic Instruction Code....
, J, MATLABMATLABMATLAB is a numerical computing environment and fourth-generation programming language. Developed by MathWorks, MATLAB allows matrix manipulations, plotting of functions and data, implementation of algorithms, creation of user interfaces, and interfacing with programs written in other languages,...
, RR (programming language)R is a programming language and software environment for statistical computing and graphics. The R language is widely used among statisticians for developing statistical software, and R is widely used for statistical software development and data analysis....
, Microsoft ExcelMicrosoft ExcelMicrosoft Excel is a proprietary commercial spreadsheet application written and distributed by Microsoft for Microsoft Windows and Mac OS X. It features calculation, graphing tools, pivot tables, and a macro programming language called Visual Basic for Applications...
, TeXTeXTeX is a typesetting system designed and mostly written by Donald Knuth and released in 1978. Within the typesetting system, its name is formatted as ....
(and its derivatives), TI-BASICTI-BASICTI-BASIC is the unofficial name of a BASIC-like language built into Texas Instruments 's graphing calculators, including the TI-83 series, TI-84 Plus series, TI-89 series, TI-92 series , TI-73, and TI-Nspire...
, bcBc programming languagebc, for bench calculator, is "an arbitrary precision calculator language" with syntax similar to the C programming language. bc is typically used as either a mathematical scripting language or as an interactive mathematical shell....
(for integer exponents), HaskellHaskell (programming language)Haskell is a standardized, general-purpose purely functional programming language, with non-strict semantics and strong static typing. It is named after logician Haskell Curry. In Haskell, "a function is a first-class citizen" of the programming language. As a functional programming language, the...
(for nonnegative integer exponents), Lua, ASPActive Server PagesActive Server Pages , also known as Classic ASP or ASP Classic, was Microsoft's first server-side script engine for dynamically-generated Web pages. Initially released as an add-on to Internet Information Services via the Windows NT 4.0 Option Pack Active Server Pages (ASP), also known as Classic...
and most computer algebra systemComputer algebra systemA computer algebra system is a software program that facilitates symbolic mathematics. The core functionality of a CAS is manipulation of mathematical expressions in symbolic form.-Symbolic manipulations:...
s -
x ^^ y: Haskell (for fractional base, integer exponents), DD (programming language)The D programming language is an object-oriented, imperative, multi-paradigm, system programming language created by Walter Bright of Digital Mars. It originated as a re-engineering of C++, but even though it is mainly influenced by that language, it is not a variant of C++... -
x ** y: AdaAda (programming language)Ada is a structured, statically typed, imperative, wide-spectrum, and object-oriented high-level computer programming language, extended from Pascal and other languages...
, Bash, COBOLCOBOLCOBOL is one of the oldest programming languages. Its name is an acronym for COmmon Business-Oriented Language, defining its primary domain in business, finance, and administrative systems for companies and governments....
, FortranFortranFortran is a general-purpose, procedural, imperative programming language that is especially suited to numeric computation and scientific computing...
, FoxProFoxPro 2FoxPro is a text-based procedurally-oriented programming language and DBMS, originally published by Fox Software and later by Microsoft, for MS-DOS, MS Windows, Apple Macintosh, and UNIX....
, GnuplotGnuplot- License :Despite gnuplot's name, it is not part of or related to the GNU system and it is not distributed under the GNU General Public License .However, some GNU packages do use gnuplot....
, OCaml, PerlPerlPerl is a high-level, general-purpose, interpreted, dynamic programming language. Perl was originally developed by Larry Wall in 1987 as a general-purpose Unix scripting language to make report processing easier. Since then, it has undergone many changes and revisions and become widely popular...
, PL/IPL/IPL/I is a procedural, imperative computer programming language designed for scientific, engineering, business and systems programming applications...
, PythonPython (programming language)Python is a general-purpose, high-level programming language whose design philosophy emphasizes code readability. Python claims to "[combine] remarkable power with very clear syntax", and its standard library is large and comprehensive...
, RexxREXXREXX is an interpreted programming language that was developed at IBM. It is a structured high-level programming language that was designed to be both easy to learn and easy to read...
, RubyRuby (programming language)Ruby is a dynamic, reflective, general-purpose object-oriented programming language that combines syntax inspired by Perl with Smalltalk-like features. Ruby originated in Japan during the mid-1990s and was first developed and designed by Yukihiro "Matz" Matsumoto...
, SAS, TclTclTcl is a scripting language created by John Ousterhout. Originally "born out of frustration", according to the author, with programmers devising their own languages intended to be embedded into applications, Tcl gained acceptance on its own...
, ABAPABAPABAP , is a high-level programming language created by the German software company SAP...
, Haskell (for floating-point exponents), Turing, VHDL -
x⋆y: APL -
Power(x, y): Microsoft Excel, Delphi/Pascal (declared in "Math"-unit) -
pow(x, y): CC (programming language)C is a general-purpose computer programming language developed between 1969 and 1973 by Dennis Ritchie at the Bell Telephone Laboratories for use with the Unix operating system....
, C++C++C++ is a statically typed, free-form, multi-paradigm, compiled, general-purpose programming language. It is regarded as an intermediate-level language, as it comprises a combination of both high-level and low-level language features. It was developed by Bjarne Stroustrup starting in 1979 at Bell...
, PHPPHPPHP is a general-purpose server-side scripting language originally designed for web development to produce dynamic web pages. For this purpose, PHP code is embedded into the HTML source document and interpreted by a web server with a PHP processor module, which generates the web page document...
, TclTclTcl is a scripting language created by John Ousterhout. Originally "born out of frustration", according to the author, with programmers devising their own languages intended to be embedded into applications, Tcl gained acceptance on its own...
, Python -
math.pow(x, y): Python (always fractional results) -
Math.pow(x, y): JavaJava (programming language)Java is a programming language originally developed by James Gosling at Sun Microsystems and released in 1995 as a core component of Sun Microsystems' Java platform. The language derives much of its syntax from C and C++ but has a simpler object model and fewer low-level facilities...
, JavaScriptJavaScriptJavaScript is a prototype-based scripting language that is dynamic, weakly typed and has first-class functions. It is a multi-paradigm language, supporting object-oriented, imperative, and functional programming styles....
, Modula-3Modula-3In computer science, Modula-3 is a programming language conceived as a successor to an upgraded version of Modula-2 known as Modula-2+. While it has been influential in research circles it has not been adopted widely in industry...
, Standard MLStandard MLStandard ML is a general-purpose, modular, functional programming language with compile-time type checking and type inference. It is popular among compiler writers and programming language researchers, as well as in the development of theorem provers.SML is a modern descendant of the ML... -
Math.Pow(x, y)orBigInteger.Pow(x, y): C# (and other languages using the BCLBase Class LibraryThe Base Class Library is a standard library available to all languages using the .NET Framework. .NET includes the BCL in order to encapsulate a large number of common functions, such as file reading and writing, graphic rendering, database interaction, and XML document manipulation, which makes...
) -
(expt x y): Common LispCommon LispCommon Lisp, commonly abbreviated CL, is a dialect of the Lisp programming language, published in ANSI standard document ANSI INCITS 226-1994 , . From the ANSI Common Lisp standard the Common Lisp HyperSpec has been derived for use with web browsers...
, Scheme -
math:pow(x, y): Erlang
In Bash, C, C++, C#, Java, JavaScript, Perl, PHP, Python and Ruby, the symbol ^ represents bitwise XOR. In Pascal, it represents indirection
Indirection
In computer programming, indirection is the ability to reference something using a name, reference, or container instead of the value itself. The most common form of indirection is the act of manipulating a value through its memory address. For example, accessing a variable through the use of a...
. In OCaml and Standard ML, it represents string concatenation
Concatenation
In computer programming, string concatenation is the operation of joining two character strings end-to-end. For example, the strings "snow" and "ball" may be concatenated to give "snowball"...
.
History of the notation
The term power was used by the GreekGreek mathematics
Greek mathematics, as that term is used in this article, is the mathematics written in Greek, developed from the 7th century BC to the 4th century AD around the Eastern shores of the Mediterranean. Greek mathematicians lived in cities spread over the entire Eastern Mediterranean, from Italy to...
mathematician Euclid
Euclid
Euclid , fl. 300 BC, also known as Euclid of Alexandria, was a Greek mathematician, often referred to as the "Father of Geometry". He was active in Alexandria during the reign of Ptolemy I...
for the square of a line. In the 9th century, Muhammad ibn Mūsā al-Khwārizmī
Muhammad ibn Musa al-Khwarizmi
'There is some confusion in the literature on whether al-Khwārizmī's full name is ' or '. Ibn Khaldun notes in his encyclopedic work: "The first who wrote upon this branch was Abu ʿAbdallah al-Khowarizmi, after whom came Abu Kamil Shojaʿ ibn Aslam." . 'There is some confusion in the literature on...
used the terms mal for a square and kab for a cube, which later Islamic mathematicians represented in mathematical notation
Mathematical notation
Mathematical notation is a system of symbolic representations of mathematical objects and ideas. Mathematical notations are used in mathematics, the physical sciences, engineering, and economics...
as m and k, respectively, by the 15th century, as seen in the work of Abū al-Hasan ibn Alī al-Qalasādī
Abu al-Hasan ibn Ali al-Qalasadi
Abū al-Ḥasan ibn ʿAlī ibn Muḥammad ibn ʿAlī al-Qalaṣādī was a Muslim mathematician from Al-Andalus specializing in Islamic inheritance jurisprudence...
.
Nicolas Chuquet
Nicolas Chuquet
Nicolas Chuquet was a French mathematician whose great work, Triparty en la science des nombres , was unpublished in his lifetime...
used a form of exponential notation in the 15th century, which was later used by Henricus Grammateus
Henricus Grammateus
Henricus Grammateus was a German mathematician. In 1518 he published details of a new musical temperament, which is now named after him, for the harpsichord...
and Michael Stifel
Michael Stifel
Michael Stifel or Styfel was a German monk and mathematician. He was an Augustinian who became an early supporter of Martin Luther. Stifel was later appointed professor of mathematics at Jena University...
in the 16th century. Samuel Jeake
Samuel Jeake
Samuel Jeake , dubbed the elder to distinguish him from his son, was a merchant, Nonconformist and astrologer from Rye, East Sussex, England. He is primarily known for his extensive diaries, which are today considered a valuable historical resource...
introduced the term indices in 1696. In the 16th century Robert Recorde
Robert Recorde
Robert Recorde was a Welsh physician and mathematician. He introduced the "equals" sign in 1557.-Biography:A member of a respectable family of Tenby, Wales, he entered the University of Oxford about 1525, and was elected a fellow of All Souls College in 1531...
used the terms square, cube, zenzizenzic (fourth power), surfolide (fifth), zenzicube (sixth), second surfolide (seventh) and Zenzizenzizenzic
Zenzizenzizenzic
Zenzizenzizenzic is an obsolete form of mathematical notation representing the eighth power of a number , dating from a time when powers were written out in words rather than as superscript numbers...
(eighth). Biquadrate has been used to refer to the fourth power as well.
Some mathematicians (e.g., Isaac Newton
Isaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
) used exponents only for powers greater than two, preferring to represent squares as repeated multiplication. Thus they would write polynomials, for example, as ax + bxx + cx3 + d.
Another historical synonym, involution, is now rare and should not be confused with its more common meaning.
See also
- Complex logarithmComplex logarithmIn complex analysis, a complex logarithm function is an "inverse" of the complex exponential function, just as the natural logarithm ln x is the inverse of the real exponential function ex. Thus, a logarithm of z is a complex number w such that ew = z. The notation for such a w is log z...
- Exponential decay
- Exponential functionExponential functionIn mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
- Exponential growthExponential growthExponential growth occurs when the growth rate of a mathematical function is proportional to the function's current value...
- List of exponential topics
- LogarithmLogarithmThe logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
- Modular exponentiationModular exponentiationModular exponentiation is a type of exponentiation performed over a modulus. It is particularly useful in computer science, especially in the field of cryptography....
- Nth rootNth rootIn mathematics, the nth root of a number x is a number r which, when raised to the power of n, equals xr^n = x,where n is the degree of the root...
- TetrationTetrationIn mathematics, tetration is an iterated exponential and is the next hyper operator after exponentiation. The word tetration was coined by English mathematician Reuben Louis Goodstein from tetra- and iteration. Tetration is used for the notation of very large numbers...
- Unicode subscripts and superscriptsUnicode subscripts and superscriptsUnicode has subscripted and superscripted versions of a number of characters including a full set of arabic numerals. These characters allow any polynomial, chemical and certain other equations to be represented in plain text without using any form of markup like HTML or TeX.The World Wide Web...
External links
- sci.math FAQ: What is 00?
- Laws of Exponents with derivation and examples
- What does 0^0 (zero to the zeroth power) equal? on AskAMathematician.com