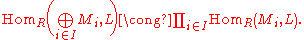Direct sum of modules
Encyclopedia
In abstract algebra
, the direct sum is a construction which combines several modules
into a new, larger module. The result of the direct summation of modules is the "smallest general" module which contains the given modules as submodules
. This is an example of a coproduct
. Contrast with the direct product
, which is the dual notion.
The most familiar examples of this construction occur when considering vector space
s (modules over a field
) and abelian group
s (modules over the ring Z of integer
s). The construction may also be extended
to cover Banach space
s and Hilbert space
s.
s over the field
K. The cartesian product
V × W can be given the structure of a vector space over K by defining the operations componentwise:
for v, v1, v2 ∈ V, w, w1, w2 ∈ W, and α ∈ K.
The resulting vector space is called the direct sum of V and W and is usually denoted by a plus symbol inside a circle:

It is customary to write the elements of an ordered sum not as ordered pairs (v, w), but as a sum v + w.
The subspace V × {0} of V ⊕ W is isomorphic to V and is often identified with V; similarly for {0} × W and W. (See internal direct sum below.) With this identification, every element of V ⊕ W can be written in one and only one way as the sum of an element of V and an element of W. The dimension of V ⊕ W is equal to the sum of the dimensions of V and W.
This construction readily generalises to any finite number of vector spaces.
s G and H which are written additively, the direct product
of G and H is also called a direct sum . Thus the cartesian product
G × H is equipped with the structure of an abelian group by defining the operations componentwise:
for g1, g2 in G, and h1, h2 in H.
Integral multiples are similarly defined componentwise by
for g in G, h in H, and n an integer
. This parallels the extension of the scalar product of vector spaces to the direct sum above.
The resulting abelian group is called the direct sum of G and H and is usually denoted by a plus symbol inside a circle:

It is customary to write the elements of an ordered sum not as ordered pairs (g, h), but as a sum g + h.
The subgroup G × {0} of G ⊕ H is isomorphic to G and is often identified with G; similarly for {0} × H and H. (See internal direct sum below.) With this identification, it is true that every element of G ⊕ H can be written in one and only one way as the sum of an element of G and an element of H. The rank
of G ⊕ H is equal to the sum of the ranks of G and H.
This construction readily generalises to any finite number of abelian groups.
. Additionally, by modifying the definition one can accommodate the direct sum of an infinite family of modules. The precise definition is as follows .
Let R be a ring, and {Mi : i ∈ I} a family of left R-modules indexed by the set I. The direct sum of {Mi} is then defined to be the set of all sequences where
where 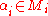 and
and  for cofinitely many indices i. (The direct product
for cofinitely many indices i. (The direct product
is analogous but the indices do not need to cofinitely vanish.)
It can also be defined as functions
α from I to the disjoint union
of the modules Mi such that α(i) ∈ Mi for all i ∈ I and α(i) = 0 for cofinitely many indices i. These functions can equivalently be regarded as finitely supported sections of the fiber bundle
over the index set I, with the fiber over being
being 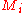 .
.
This set inherits the module structure via component-wise addition and scalar multiplication. Explicitly, two such sequences (or functions) α and β can be added by writing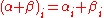 for all i (note that this is again zero for all but finitely many indices), and such a function can be multiplied with an element r from R by defining
for all i (note that this is again zero for all but finitely many indices), and such a function can be multiplied with an element r from R by defining  for all i. In this way, the direct sum becomes a left R-module, and it is denoted
for all i. In this way, the direct sum becomes a left R-module, and it is denoted

It is customary to write the sequence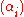 as a sum
as a sum 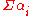 . Sometimes a primed summation
. Sometimes a primed summation  is used to indicate that cofinitely many of the terms are zero.
is used to indicate that cofinitely many of the terms are zero.
A submodule N of M is a direct summand of M if there exists some other submodule N′ of M such that M is the internal direct sum of N and N′. In this case, N and N′ are complementary subspaces.
, the direct sum is a coproduct
and hence a colimit
in the category of left R-modules, which means that it is characterized by the following universal property
. For every i in I, consider the natural embedding
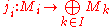
which sends the elements of Mi to those functions which are zero for all arguments but i. If fi : Mi → M are arbitrary R-linear maps for every i, then there exists precisely one R-linear map
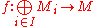
such that f o ji = fi for all i.
Dually, the direct product
is the product
.
, in that the addition of objects is defined, but not subtraction. In fact, subtraction can be defined, and every commutative monoid can be extended to an abelian group
. This extension is known as the Grothendieck group
. The extension is done by defining equivalence classes of pairs of objects, which allows certain pairs to be treated as inverses. The construction, detailed in the article on the Grothendieck group, is "universal", in that it has the universal property
of being unique, and homomorphic to any other embedding of an abelian monoid in an abelian group.
or an inner product), then the direct sum of the modules can often be made to carry this additional structure, as well. In this case, we obtain the coproduct
in the appropriate category of all objects carrying the additional structure. Three prominent examples occur for algebras over a field
, Banach space
s and Hilbert space
s.
X and Y is the direct sum as vector spaces, with product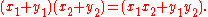
Consider these classical examples: has been studied as split-complex number
has been studied as split-complex number
s, is the algebra of tessarine
is the algebra of tessarine
s introduced by James Cockle in 1848, and , called the split-biquaternions, was introduced by William Kingdon Clifford
, called the split-biquaternions, was introduced by William Kingdon Clifford
in 1873.
Joseph Wedderburn
exploited the concept of a direct sum of algebras in his classification of hypercomplex number
s. See his Lectures on Matrices (1934), page 151.
Wedderburn makes clear the distinction between a direct sum and a direct product of algebras: For the direct sum the field of scalars acts jointly on both parts: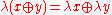 while for the direct product a scalar factor may be collected alternately with the parts, but not both:
while for the direct product a scalar factor may be collected alternately with the parts, but not both: .
.
Ian R. Porteous
uses the three direct sums above, denoting them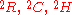 , as rings of scalars in his analysis of Clifford Algebras and the Classical Groups (1995).
, as rings of scalars in his analysis of Clifford Algebras and the Classical Groups (1995).
The direct sum of two Banach space
s X and Y is the direct sum of X and Y considered as vector spaces, with the norm ||(x,y)|| = ||x||X + ||y||Y for all x in X and y in Y.
Generally, if Xi is a collection of Banach spaces, where i traverses the index set
I, then the direct sum ⊕i∈I Xi is a module consisting of all functions x defined over
I such that x(i) ∈ Xi for all i ∈ I and
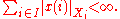
The norm is given by the sum above. The direct sum with this norm is again a Banach space.
For example, if we take the index set I = N and Xi = R, then the direct sum ⊕i∈N is the space l1, which consists of all the sequences (ai) of reals with finite norm ||a|| = ∑i |ai|.
A closed subspace A of a Banach space X is complemented if there is another closed subspace B of X such that X is equal to the internal direct sum . Note that not every closed subspace is complimented, eg. c0 is not complimented in
. Note that not every closed subspace is complimented, eg. c0 is not complimented in 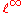 .
.
s H1,...,Hn are given, one can construct their direct sum as above (since they are vector spaces), and then turn the direct sum into a Hilbert space by defining the inner product as:

This turns the direct sum into a Hilbert space which contains the given Hilbert spaces as mutually orthogonal subspaces.
If infinitely many Hilbert spaces Hi for i in I are given, we can carry out the same construction; notice that when defining the inner product, only finitely many summands will be non-zero. However, the result will only be an inner product space
and it won't be complete. We then define the direct sum of the Hilbert spaces Hi to be the completion of this inner product space.
Alternatively and equivalently, one can define the direct sum of the Hilbert spaces Hi as the space of all functions α with domain I, such that α(i) is an element of Hi for every i in I and:

The inner product of two such function α and β is then defined as:

This space is complete and we get a Hilbert space.
For example, if we take the index set I = N and Xi = R, then the direct sum ⊕i∈N Xi is the space l2, which consists of all the sequences (ai) of reals with finite norm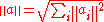 . Comparing this with the example for Banach spaces, we see that the Banach space direct sum and the Hilbert space direct sum are not necessarily the same. But if there are only finitely many summands, then the Banach space direct sum is isomorphic to the Hilbert space direct sum, although the norm will be different.
. Comparing this with the example for Banach spaces, we see that the Banach space direct sum and the Hilbert space direct sum are not necessarily the same. But if there are only finitely many summands, then the Banach space direct sum is isomorphic to the Hilbert space direct sum, although the norm will be different.
Every Hilbert space is isomorphic to a direct sum of sufficiently many copies of the base field (either R or C). This is equivalent to the assertion that every Hilbert space has an orthonormal basis. More generally, every closed subspace of a Hilbert space is complemented: it admits an orthogonal complement. Conversely, the Lindenstrauss–Tzafriri theorem asserts that if every closed subspace of a Banach space is complemented, then the Banach space is isomorphic (topologically) to a Hilbert space.
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, the direct sum is a construction which combines several modules
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
into a new, larger module. The result of the direct summation of modules is the "smallest general" module which contains the given modules as submodules
. This is an example of a coproduct
Coproduct
In category theory, the coproduct, or categorical sum, is the category-theoretic construction which includes the disjoint union of sets and of topological spaces, the free product of groups, and the direct sum of modules and vector spaces. The coproduct of a family of objects is essentially the...
. Contrast with the direct product
Direct product
In mathematics, one can often define a direct product of objectsalready known, giving a new one. This is generally the Cartesian product of the underlying sets, together with a suitably defined structure on the product set....
, which is the dual notion.
The most familiar examples of this construction occur when considering vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s (modules over a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
) and abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s (modules over the ring Z of integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s). The construction may also be extended
Algebraic extension
In abstract algebra, a field extension L/K is called algebraic if every element of L is algebraic over K, i.e. if every element of L is a root of some non-zero polynomial with coefficients in K. Field extensions that are not algebraic, i.e...
to cover Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
s and Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
s.
Construction for vector spaces and abelian groups
We give the construction first in these two cases, under the assumption that we have only two objects. Then we generalise to an arbitrary family of arbitrary modules. The key elements of the general construction are more clearly identified by considering these two cases in depth.Construction for two vector spaces
Suppose V and W are vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s over the field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
K. The cartesian product
Cartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
V × W can be given the structure of a vector space over K by defining the operations componentwise:
- (v1, w1) + (v2, w2) = (v1 + v2, w1 + w2)
- α (v, w) = (α v, α w)
for v, v1, v2 ∈ V, w, w1, w2 ∈ W, and α ∈ K.
The resulting vector space is called the direct sum of V and W and is usually denoted by a plus symbol inside a circle:

It is customary to write the elements of an ordered sum not as ordered pairs (v, w), but as a sum v + w.
The subspace V × {0} of V ⊕ W is isomorphic to V and is often identified with V; similarly for {0} × W and W. (See internal direct sum below.) With this identification, every element of V ⊕ W can be written in one and only one way as the sum of an element of V and an element of W. The dimension of V ⊕ W is equal to the sum of the dimensions of V and W.
This construction readily generalises to any finite number of vector spaces.
Construction for two abelian groups
For abelian groupAbelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s G and H which are written additively, the direct product
Direct product
In mathematics, one can often define a direct product of objectsalready known, giving a new one. This is generally the Cartesian product of the underlying sets, together with a suitably defined structure on the product set....
of G and H is also called a direct sum . Thus the cartesian product
Cartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
G × H is equipped with the structure of an abelian group by defining the operations componentwise:
- (g1, h1) + (g2, h2) = (g1 + g2, h1 + h2)
for g1, g2 in G, and h1, h2 in H.
Integral multiples are similarly defined componentwise by
- n(g, h) = (ng, nh)
for g in G, h in H, and n an integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
. This parallels the extension of the scalar product of vector spaces to the direct sum above.
The resulting abelian group is called the direct sum of G and H and is usually denoted by a plus symbol inside a circle:

It is customary to write the elements of an ordered sum not as ordered pairs (g, h), but as a sum g + h.
The subgroup G × {0} of G ⊕ H is isomorphic to G and is often identified with G; similarly for {0} × H and H. (See internal direct sum below.) With this identification, it is true that every element of G ⊕ H can be written in one and only one way as the sum of an element of G and an element of H. The rank
Rank of an abelian group
In mathematics, the rank, Prüfer rank, or torsion-free rank of an abelian group A is the cardinality of a maximal linearly independent subset. The rank of A determines the size of the largest free abelian group contained in A. If A is torsion-free then it embeds into a vector space over the...
of G ⊕ H is equal to the sum of the ranks of G and H.
This construction readily generalises to any finite number of abelian groups.
Construction for an arbitrary family of modules
One should notice a clear similarity between the definitions of the direct sum of two vector spaces and of two abelian groups. In fact, each is a special case of the construction of the direct sum of two modulesModule (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
. Additionally, by modifying the definition one can accommodate the direct sum of an infinite family of modules. The precise definition is as follows .
Let R be a ring, and {Mi : i ∈ I} a family of left R-modules indexed by the set I. The direct sum of {Mi} is then defined to be the set of all sequences
 where
where 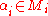 and
and  for cofinitely many indices i. (The direct product
for cofinitely many indices i. (The direct productDirect product
In mathematics, one can often define a direct product of objectsalready known, giving a new one. This is generally the Cartesian product of the underlying sets, together with a suitably defined structure on the product set....
is analogous but the indices do not need to cofinitely vanish.)
It can also be defined as functions
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
α from I to the disjoint union
Disjoint union
In mathematics, the term disjoint union may refer to one of two different concepts:* In set theory, a disjoint union is a modified union operation that indexes the elements according to which set they originated in; disjoint sets have no element in common.* In probability theory , a disjoint union...
of the modules Mi such that α(i) ∈ Mi for all i ∈ I and α(i) = 0 for cofinitely many indices i. These functions can equivalently be regarded as finitely supported sections of the fiber bundle
Fiber bundle
In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
over the index set I, with the fiber over
 being
being 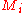 .
.This set inherits the module structure via component-wise addition and scalar multiplication. Explicitly, two such sequences (or functions) α and β can be added by writing
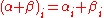 for all i (note that this is again zero for all but finitely many indices), and such a function can be multiplied with an element r from R by defining
for all i (note that this is again zero for all but finitely many indices), and such a function can be multiplied with an element r from R by defining  for all i. In this way, the direct sum becomes a left R-module, and it is denoted
for all i. In this way, the direct sum becomes a left R-module, and it is denoted
It is customary to write the sequence
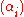 as a sum
as a sum 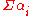 . Sometimes a primed summation
. Sometimes a primed summation  is used to indicate that cofinitely many of the terms are zero.
is used to indicate that cofinitely many of the terms are zero.Properties
- The direct sum is a submodule of the direct productDirect productIn mathematics, one can often define a direct product of objectsalready known, giving a new one. This is generally the Cartesian product of the underlying sets, together with a suitably defined structure on the product set....
of the modules Mi . The direct product is the set of all functions α from I to the disjoint union of the modules Mi with α(i)∈Mi, but not necessarily vanishing for all but finitely many i. If the index set I is finite, then the direct sum and the direct product are equal. - Each of the modules Mi may be identified with the submodule of the direct sum consisting of those functions which vanish on all indices different from i. With these identifications, every element x of the direct sum can be written in one and only one way as a sum of finitely many elements from the modules Mi.
- If the Mi are actually vector spaces, then the dimension of the direct sum is equal to the sum of the dimensions of the Mi. The same is true for the rank of abelian groupsRank of an abelian groupIn mathematics, the rank, Prüfer rank, or torsion-free rank of an abelian group A is the cardinality of a maximal linearly independent subset. The rank of A determines the size of the largest free abelian group contained in A. If A is torsion-free then it embeds into a vector space over the...
and the length of modulesLength of a moduleIn abstract algebra, the length of a module is a measure of the module's "size". It is defined to be the length of the longest chain of submodules and is a generalization of the concept of dimension for vector spaces...
. - Every vector space over the field K is isomorphic to a direct sum of sufficiently many copies of K, so in a sense only these direct sums have to be considered. This is not true for modules over arbitrary rings.
- The tensor productTensor productIn mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
distributes over direct sums in the following sense: if N is some right R-module, then the direct sum of the tensor products of N with Mi (which are abelian groups) is naturally isomorphic to the tensor product of N with the direct sum of the Mi. - Direct sums are also commutative and associative (up to isomorphism), meaning that it doesn't matter in which order one forms the direct sum.
- The group of R-linear homomorphisms from the direct sum to some left R-module L is naturally isomorphic to the direct productDirect productIn mathematics, one can often define a direct product of objectsalready known, giving a new one. This is generally the Cartesian product of the underlying sets, together with a suitably defined structure on the product set....
of the groups of R-linear homomorphisms from Mi to L:-
- Indeed, there is clearly a homomorphism τ from the left hand side to the right hand side, where τ(θ)(i) is the R-linear homomorphism sending x∈Mi to θ(x) (using the natural inclusion of Mi into the direct sum). The inverse of the homomorphism τ is defined by
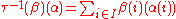
- for any α in the direct sum of the modules Mi. The key point is that the definition of τ−1 makes sense because α(i) is zero for all but finitely many i, and so the sum is finite.
- In particular, the dual vector spaceDual spaceIn mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
of a direct sum of vector spaces is isomorphic to the direct productDirect productIn mathematics, one can often define a direct product of objectsalready known, giving a new one. This is generally the Cartesian product of the underlying sets, together with a suitably defined structure on the product set....
of the duals of those spaces.
-
- The finite direct sum of modules is a biproductBiproductIn category theory and its applications to mathematics, a biproduct of a finite collection of objects in a category with zero object is both a product and a coproduct. In a preadditive category the notions of product and coproduct coincide for finite collections of objects...
: If-
- are the canonical projection mappings and
- are the inclusion mappings, then
- equals the identity morphism of A1 ⊕ ··· ⊕ An, and
- is the identity morphism of Ak in the case l=k, and is the zero map otherwise.
-
Internal direct sum
Suppose M is some R-module, and Mi is a submodule of M for every i in I. If every x in M can be written in one and only one way as a sum of finitely many elements of the Mi, then we say that M is the internal direct sum of the submodules Mi . In this case, M is naturally isomorphic to the (external) direct sum of the Mi as defined above .A submodule N of M is a direct summand of M if there exists some other submodule N′ of M such that M is the internal direct sum of N and N′. In this case, N and N′ are complementary subspaces.
Universal property
In the language of category theoryCategory theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, the direct sum is a coproduct
Coproduct
In category theory, the coproduct, or categorical sum, is the category-theoretic construction which includes the disjoint union of sets and of topological spaces, the free product of groups, and the direct sum of modules and vector spaces. The coproduct of a family of objects is essentially the...
and hence a colimit
Limit (category theory)
In category theory, a branch of mathematics, the abstract notion of a limit captures the essential properties of universal constructions such as products and inverse limits....
in the category of left R-modules, which means that it is characterized by the following universal property
Universal property
In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
. For every i in I, consider the natural embedding
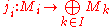
which sends the elements of Mi to those functions which are zero for all arguments but i. If fi : Mi → M are arbitrary R-linear maps for every i, then there exists precisely one R-linear map
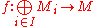
such that f o ji = fi for all i.
Dually, the direct product
Direct product
In mathematics, one can often define a direct product of objectsalready known, giving a new one. This is generally the Cartesian product of the underlying sets, together with a suitably defined structure on the product set....
is the product
Product (category theory)
In category theory, the product of two objects in a category is a notion designed to capture the essence behind constructions in other areas of mathematics such as the cartesian product of sets, the direct product of groups, the direct product of rings and the product of topological spaces...
.
Grothendieck group
The direct sum gives a collection of objects the structure of a commutative monoidMonoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
, in that the addition of objects is defined, but not subtraction. In fact, subtraction can be defined, and every commutative monoid can be extended to an abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
. This extension is known as the Grothendieck group
Grothendieck group
In mathematics, the Grothendieck group construction in abstract algebra constructs an abelian group from a commutative monoid in the best possible way...
. The extension is done by defining equivalence classes of pairs of objects, which allows certain pairs to be treated as inverses. The construction, detailed in the article on the Grothendieck group, is "universal", in that it has the universal property
Universal property
In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
of being unique, and homomorphic to any other embedding of an abelian monoid in an abelian group.
Direct sum of modules with additional structure
If the modules we are considering carry some additional structure (e.g. a normNorm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
or an inner product), then the direct sum of the modules can often be made to carry this additional structure, as well. In this case, we obtain the coproduct
Coproduct
In category theory, the coproduct, or categorical sum, is the category-theoretic construction which includes the disjoint union of sets and of topological spaces, the free product of groups, and the direct sum of modules and vector spaces. The coproduct of a family of objects is essentially the...
in the appropriate category of all objects carrying the additional structure. Three prominent examples occur for algebras over a field
Algebra over a field
In mathematics, an algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it isan algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as...
, Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
s and Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
s.
Direct sum of algebras
A direct sum of algebrasAlgebra over a field
In mathematics, an algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it isan algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as...
X and Y is the direct sum as vector spaces, with product
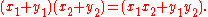
Consider these classical examples:
 has been studied as split-complex number
has been studied as split-complex numberSplit-complex number
In abstract algebra, the split-complex numbers are a two-dimensional commutative algebra over the real numbers different from the complex numbers. Every split-complex number has the formwhere x and y are real numbers...
s,
 is the algebra of tessarine
is the algebra of tessarineTessarine
In mathematics, a tessarine is a hypercomplex number of the formt = w + x i + y j + z k, \quad w, x, y, z \in Rwhere i j = j i = k, \quad i^2 = -1, \quad j^2 = +1 .The tessarines are best known for their subalgebra of real tessarines t = w + y j \ ,...
s introduced by James Cockle in 1848, and
 , called the split-biquaternions, was introduced by William Kingdon Clifford
, called the split-biquaternions, was introduced by William Kingdon CliffordWilliam Kingdon Clifford
William Kingdon Clifford FRS was an English mathematician and philosopher. Building on the work of Hermann Grassmann, he introduced what is now termed geometric algebra, a special case of the Clifford algebra named in his honour, with interesting applications in contemporary mathematical physics...
in 1873.
Joseph Wedderburn
Joseph Wedderburn
Joseph Henry Maclagan Wedderburn was a Scottish mathematician, who taught at Princeton University for most of his career. A significant algebraist, he proved that a finite division algebra is a field, and part of the Artin–Wedderburn theorem on simple algebras...
exploited the concept of a direct sum of algebras in his classification of hypercomplex number
Hypercomplex number
In mathematics, a hypercomplex number is a traditional term for an element of an algebra over a field where the field is the real numbers or the complex numbers. In the nineteenth century number systems called quaternions, tessarines, coquaternions, biquaternions, and octonions became established...
s. See his Lectures on Matrices (1934), page 151.
Wedderburn makes clear the distinction between a direct sum and a direct product of algebras: For the direct sum the field of scalars acts jointly on both parts:
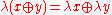 while for the direct product a scalar factor may be collected alternately with the parts, but not both:
while for the direct product a scalar factor may be collected alternately with the parts, but not both: .
.Ian R. Porteous
Ian R. Porteous
Ian Robertson Porteous was a Scottish mathematician at the University of Liverpool and an educator on Merseyside. He is best known for three books on geometry and modern algebra...
uses the three direct sums above, denoting them
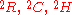 , as rings of scalars in his analysis of Clifford Algebras and the Classical Groups (1995).
, as rings of scalars in his analysis of Clifford Algebras and the Classical Groups (1995).Direct sum of Banach spaces
The direct sum of two Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
s X and Y is the direct sum of X and Y considered as vector spaces, with the norm ||(x,y)|| = ||x||X + ||y||Y for all x in X and y in Y.
Generally, if Xi is a collection of Banach spaces, where i traverses the index set
Index set
In mathematics, the elements of a set A may be indexed or labeled by means of a set J that is on that account called an index set...
I, then the direct sum ⊕i∈I Xi is a module consisting of all functions x defined over
Domain
-General:*Territory , a non-sovereign geographic area which has come under the authority of another government*Public domain, a body of works and knowledge without proprietary interest...
I such that x(i) ∈ Xi for all i ∈ I and
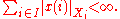
The norm is given by the sum above. The direct sum with this norm is again a Banach space.
For example, if we take the index set I = N and Xi = R, then the direct sum ⊕i∈N is the space l1, which consists of all the sequences (ai) of reals with finite norm ||a|| = ∑i |ai|.
A closed subspace A of a Banach space X is complemented if there is another closed subspace B of X such that X is equal to the internal direct sum
 . Note that not every closed subspace is complimented, eg. c0 is not complimented in
. Note that not every closed subspace is complimented, eg. c0 is not complimented in 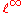 .
.Direct sum of Hilbert spaces
If finitely many Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
s H1,...,Hn are given, one can construct their direct sum as above (since they are vector spaces), and then turn the direct sum into a Hilbert space by defining the inner product as:

This turns the direct sum into a Hilbert space which contains the given Hilbert spaces as mutually orthogonal subspaces.
If infinitely many Hilbert spaces Hi for i in I are given, we can carry out the same construction; notice that when defining the inner product, only finitely many summands will be non-zero. However, the result will only be an inner product space
Inner product space
In mathematics, an inner product space is a vector space with an additional structure called an inner product. This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors...
and it won't be complete. We then define the direct sum of the Hilbert spaces Hi to be the completion of this inner product space.
Alternatively and equivalently, one can define the direct sum of the Hilbert spaces Hi as the space of all functions α with domain I, such that α(i) is an element of Hi for every i in I and:

The inner product of two such function α and β is then defined as:

This space is complete and we get a Hilbert space.
For example, if we take the index set I = N and Xi = R, then the direct sum ⊕i∈N Xi is the space l2, which consists of all the sequences (ai) of reals with finite norm
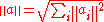 . Comparing this with the example for Banach spaces, we see that the Banach space direct sum and the Hilbert space direct sum are not necessarily the same. But if there are only finitely many summands, then the Banach space direct sum is isomorphic to the Hilbert space direct sum, although the norm will be different.
. Comparing this with the example for Banach spaces, we see that the Banach space direct sum and the Hilbert space direct sum are not necessarily the same. But if there are only finitely many summands, then the Banach space direct sum is isomorphic to the Hilbert space direct sum, although the norm will be different.Every Hilbert space is isomorphic to a direct sum of sufficiently many copies of the base field (either R or C). This is equivalent to the assertion that every Hilbert space has an orthonormal basis. More generally, every closed subspace of a Hilbert space is complemented: it admits an orthogonal complement. Conversely, the Lindenstrauss–Tzafriri theorem asserts that if every closed subspace of a Banach space is complemented, then the Banach space is isomorphic (topologically) to a Hilbert space.
See also
- BiproductBiproductIn category theory and its applications to mathematics, a biproduct of a finite collection of objects in a category with zero object is both a product and a coproduct. In a preadditive category the notions of product and coproduct coincide for finite collections of objects...
- Indecomposable moduleIndecomposable moduleIn abstract algebra, a module is indecomposable if it is non-zero and cannot be written as a direct sum of two non-zero submodules.Indecomposable is a weaker notion than simple module:simple means "no proper submodule" N...
- Jordan–Hölder theorem
- Krull–Schmidt theoremKrull–Schmidt theoremIn mathematics, the Krull–Schmidt theorem states that a group subjected to certain finiteness conditions on chains of subgroups, can be uniquely written as a finite direct product of indecomposable subgroups.-Definitions:...
- Split exact sequence