Addition-chain exponentiation
Encyclopedia
In mathematics
and computer science
, optimal addition-chain exponentiation is a method of exponentiation
by positive integer
powers that requires a minimal number of multiplications. It works by creating a shortest addition chain
that generates the desired exponent. Each exponentiation in the chain can be evaluated by multiplying two of the earlier exponentiation results. More generally, addition-chain exponentiation may also refer to exponentiation by non-minimal addition chains constructed by a variety of algorithms (since a shortest addition chain is very difficult to find).
The shortest addition-chain algorithm
requires no more multiplications than binary exponentiation and usually less. The first example of where it does better is for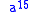
, where the binary method needs six multiplies but a shortest addition chain requires only five:
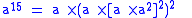(binary, 6 multiplications)
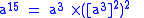(shortest addition chain, 5 multiplications).
On the other hand, the addition-chain method is much more complicated, since the determination of a shortest addition chain seems quite difficult: no efficient optimal methods are currently known for arbitrary exponents, and the related problem of finding a shortest addition chain for a given set of exponents has been proven NP-complete
. Even given a shortest chain, addition-chain exponentiation requires more memory than the binary method, because it must potentially store many previous exponents from the chain simultaneously. In practice, therefore, shortest addition-chain exponentiation is primarily used for small fixed exponents for which a shortest chain can be precomputed and is not too large.
However, there are also several methods to approximate a shortest addition chain, and which often require fewer multiplications than binary exponentiation. Indeed, binary exponentiation itself is a suboptimal addition-chain algorithm. The optimal algorithm choice depends on the context (such as the relative cost of the multiplication and the number of times a given exponent is re-used).
Note that the problem of finding the shortest addition chain cannot be solved by dynamic programming
, because it does not satisfy the assumption of optimal substructure
. That is, it is not sufficient to decompose the power into smaller powers, each of which is computed minimally, since the addition chains for the smaller powers may be related (to share computations). For example, in the shortest addition chain for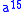
above, the subproblem for 
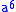must be computed as 
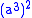since 
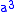is re-used (as opposed to, say, 
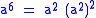, which also requires three multiplies).
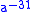, where computing 
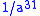by a shortest addition chain for 
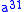requires 7 multiplications and one division, whereas the shortest addition-subtraction chain requires 5 multiplications and one division:
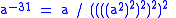(addition-subtraction chain, 5 mults + 1 div).
For exponentiation on elliptic curve
s, the inverse of a point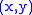
is available at no cost, since it is simply 
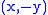, and therefore addition-subtraction chains are optimal in this context even for positive integer exponents.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, optimal addition-chain exponentiation is a method of exponentiation
Exponentiation
Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
by positive integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
powers that requires a minimal number of multiplications. It works by creating a shortest addition chain
Addition chain
In mathematics, an addition chain for computing a positive integer n can be given by a sequence of natural numbers v and a sequence of index pairs w such that each term in v is the sum of two previous terms, the indices of those terms being specified by w:Often only v is given since it is easy to...
that generates the desired exponent. Each exponentiation in the chain can be evaluated by multiplying two of the earlier exponentiation results. More generally, addition-chain exponentiation may also refer to exponentiation by non-minimal addition chains constructed by a variety of algorithms (since a shortest addition chain is very difficult to find).
The shortest addition-chain algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
requires no more multiplications than binary exponentiation and usually less. The first example of where it does better is for
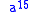, where the binary method needs six multiplies but a shortest addition chain requires only five: 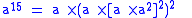(binary, 6 multiplications) 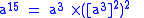(shortest addition chain, 5 multiplications).
| Number of Multiplications |
Actual Exponentiation |
Specific implementation of Addition Chains to do Exponentiation |
|---|---|---|
| 0 | a1 | a |
| 1 | a2 | a × a |
| 2 | a3 | a × a × a |
| 2 | a4 | (a × a→b) × b |
| 3 | a5 | (a × a→b) × b × a |
| 3 | a6 | (a × a→b) × b × b |
| 4 | a7 | (a × a→b) × b × b × a |
| 3 | a8 | ((a × a→b) × b→d) × d |
| 4 | a9 | (a × a × a→c) × c × c |
| 4 | a10 | ((a × a→b) × b→d) × d × b |
| 5 | a11 | ((a × a→b) × b→d) × d × b × a |
| 4 | a12 | ((a × a→b) × b→d) × d × d |
| 5 | a13 | ((a × a→b) × b→d) × d × d × a |
| 5 | a14 | ((a × a→b) × b→d) × d × d × b |
| 5 | a15 | ((a × a→b) × b × a→e) × e × e |
| 4 | a16 | (((a × a→b) × b→d) × d→h) × h |
On the other hand, the addition-chain method is much more complicated, since the determination of a shortest addition chain seems quite difficult: no efficient optimal methods are currently known for arbitrary exponents, and the related problem of finding a shortest addition chain for a given set of exponents has been proven NP-complete
NP-complete
In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
. Even given a shortest chain, addition-chain exponentiation requires more memory than the binary method, because it must potentially store many previous exponents from the chain simultaneously. In practice, therefore, shortest addition-chain exponentiation is primarily used for small fixed exponents for which a shortest chain can be precomputed and is not too large.
However, there are also several methods to approximate a shortest addition chain, and which often require fewer multiplications than binary exponentiation. Indeed, binary exponentiation itself is a suboptimal addition-chain algorithm. The optimal algorithm choice depends on the context (such as the relative cost of the multiplication and the number of times a given exponent is re-used).
Note that the problem of finding the shortest addition chain cannot be solved by dynamic programming
Dynamic programming
In mathematics and computer science, dynamic programming is a method for solving complex problems by breaking them down into simpler subproblems. It is applicable to problems exhibiting the properties of overlapping subproblems which are only slightly smaller and optimal substructure...
, because it does not satisfy the assumption of optimal substructure
Optimal substructure
In computer science, a problem is said to have optimal substructure if an optimal solution can be constructed efficiently from optimal solutions to its subproblems...
. That is, it is not sufficient to decompose the power into smaller powers, each of which is computed minimally, since the addition chains for the smaller powers may be related (to share computations). For example, in the shortest addition chain for
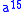above, the subproblem for 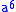must be computed as 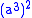since 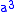is re-used (as opposed to, say, 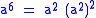, which also requires three multiplies).Addition-subtraction–chain exponentiation
If both multiplication and division are allowed, then an addition-subtraction chain may be used to obtain even fewer total multiplications+divisions (where subtraction corresponds to division). However, the slowness of division compared to multiplication makes this technique unattractive in general. For exponentiation to negative integer powers, on the other hand, since one division is required anyway, an addition-subtraction chain is often beneficial. One such example is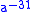, where computing 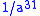by a shortest addition chain for 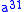requires 7 multiplications and one division, whereas the shortest addition-subtraction chain requires 5 multiplications and one division: 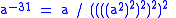(addition-subtraction chain, 5 mults + 1 div).For exponentiation on elliptic curve
Elliptic curve
In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
s, the inverse of a point
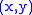is available at no cost, since it is simply 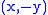, and therefore addition-subtraction chains are optimal in this context even for positive integer exponents.