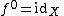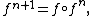Iterated function
Encyclopedia
In mathematics
, an iterated function is a function which is composed
with itself, possibly ad infinitum
, in a process called iteration
. In this process, starting from some initial value, the result of applying a given function is fed again in the function as input, and this process is repeated. The sequence of numbers that is obtained from this process is called an orbit.
Iterated functions are objects of study in computer science
, fractals, and dynamical system
s.
Let X be a set and f:X → X be a function
.
Define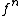
as the n-th iterate of f, where n is a non-negative integer, by:
and
where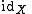
is the identity function
on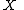
and 
denotes function composition
; that is,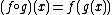
.
This is structurally identical to the property of exponentiation
that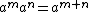
, i.e. the special case f(x)=ax.
In general, for arbitrary general (negative, non-integer, etc.) indices m and n, this relation is called the translation functional equation, cf. Schröder's equation. On a logarithmic scale, this reduces to the nesting property of Chebyshev polynomials
, Tm(Tn(x))=Tm n(x).
Because the notation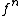
may refer to both iteration (composition) of the function 
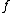and exponentiation
of the function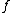
, some mathematicians choose to write 
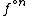for the n-th iterate of the function 
.
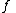The sequence of functions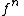
is called a Picard sequence, named after Charles Émile Picard
.
For a given x in X, the sequence
of values
is called the orbit
of x.
If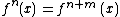
for some integer m, the orbit is called a periodic orbit. The smallest such value of m for a given x is called the period of the orbit. The point x itself is called a periodic point
. The cycle detection problem in computer science is the algorithm
ic problem of finding the first periodic point in an orbit, and the period of the orbit.
of the iterated sequence. The set of fixed points is often denoted as Fix(f). There exist a number of fixed-point theorem
s that guarantee the existence of fixed points in various situations, including the Banach fixed point theorem
and the Brouwer fixed point theorem
.
There are several techniques for convergence acceleration of the sequences produced by fixed point iteration. For example, the Aitken method applied to an iterated fixed point is known as Steffensen's method
, and produces quadratic convergence.
When the points of the orbit converge to one or more limits, the set of accumulation points of the orbit is known as the limit set
or the ω-limit set.
The ideas of attraction and repulsion generalize similarly; one may categorize iterates into stable set
s and unstable sets, according to the behaviour of small neighborhoods under iteration.
Other limiting behaviours are possible; for example, wandering points are points that move away, and never come back even close to where they started.
of a function f is a function g such that g(g(x)) = f(x). This idea can be generalized so that the iteration count n becomes a continuous parameter; in this case, such a system is called a flow
, specified by Schröder's equation. (cf. Section on #Conjugacy below.)
(1) First determine a fixed point for the function such that f(a)=a.
(2) Define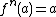
for all n belonging to the reals. This in some ways is the most natural extra condition to place upon the fractional iterates.
(3) Expand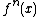
around the fixed point a as a Taylor series
.
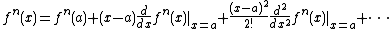
(4) Expand out: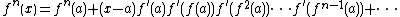
(5) Substitute in for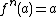
:
(6) Make use of geometric progression
to simplify terms.
(6b) There is a special case when f'(a)=1:
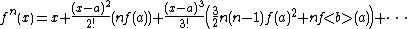
(7) When n is not an integer we make use of the power formula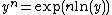
This can be carried on indefinitely although the latter terms become increasingly complicated.
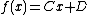gives the fixed point 
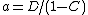and the formula above gives: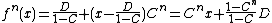
which is the correct formula. The next terms are all zero as they contain higher derivatives.
where this is done n times (and perhaps the interpolated values when n is not an integer). We have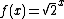 
. A fixed point is 
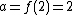. So set x=1 and 
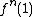expanded around the value of 2 is then an infinite series:
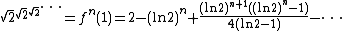
which taking just the first three terms is correct to the first decimal place when n is positive. (Using the other fixed point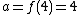
causes the series to diverge.)
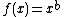we expand around the fixed point 1 to get the series:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an iterated function is a function which is composed
Function composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
with itself, possibly ad infinitum
Ad infinitum
Ad infinitum is a Latin phrase meaning "to infinity."In context, it usually means "continue forever, without limit" and thus can be used to describe a non-terminating process, a non-terminating repeating process, or a set of instructions to be repeated "forever," among other uses...
, in a process called iteration
Iteration
Iteration means the act of repeating a process usually with the aim of approaching a desired goal or target or result. Each repetition of the process is also called an "iteration," and the results of one iteration are used as the starting point for the next iteration.-Mathematics:Iteration in...
. In this process, starting from some initial value, the result of applying a given function is fed again in the function as input, and this process is repeated. The sequence of numbers that is obtained from this process is called an orbit.
Iterated functions are objects of study in computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, fractals, and dynamical system
Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
s.
Definition
The formal definition of an iterated function on a set X follows:Let X be a set and f:X → X be a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
.
Define
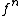as the n-th iterate of f, where n is a non-negative integer, by:
and
where
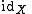is the identity functionIdentity function
In mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...
on
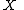and denotes function compositionFunction composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
; that is,
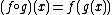.Abelian property and Iteration sequences
In general, the following identity holds for all non-negative integers m and n,
This is structurally identical to the property of exponentiation
Exponentiation
Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
that
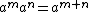, i.e. the special case f(x)=ax.In general, for arbitrary general (negative, non-integer, etc.) indices m and n, this relation is called the translation functional equation, cf. Schröder's equation. On a logarithmic scale, this reduces to the nesting property of Chebyshev polynomials
Chebyshev polynomials
In mathematics the Chebyshev polynomials, named after Pafnuty Chebyshev, are a sequence of orthogonal polynomials which are related to de Moivre's formula and which can be defined recursively. One usually distinguishes between Chebyshev polynomials of the first kind which are denoted Tn and...
, Tm(Tn(x))=Tm n(x).
Because the notation
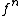may refer to both iteration (composition) of the function 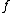and exponentiationExponentiation
Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
of the function
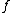, some mathematicians choose to write 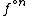for the n-th iterate of the function 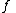.The sequence of functions
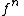is called a Picard sequence, named after Charles Émile PicardCharles Émile Picard
Charles Émile Picard FRS was a French mathematician. He was elected the fifteenth member to occupy seat 1 of the Académie Française in 1924.- Biography :...
.
For a given x in X, the sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
of values
is called the orbitOrbit (dynamics)
In mathematics, in the study of dynamical systems, an orbit is a collection of points related by the evolution function of the dynamical system. The orbit is a subset of the phase space and the set of all orbits is a partition of the phase space, that is different orbits do not intersect in the...
of x.
If
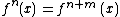for some integer m, the orbit is called a periodic orbit. The smallest such value of m for a given x is called the period of the orbit. The point x itself is called a periodic pointPeriodic point
In mathematics, in the study of iterated functions and dynamical systems, a periodic point of a function is a point which the system returns to after a certain number of function iterations or a certain amount of time.- Iterated functions :...
. The cycle detection problem in computer science is the algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
ic problem of finding the first periodic point in an orbit, and the period of the orbit.
Fixed points
If f(x) = x for some x in X, then x is called a fixed pointFixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
of the iterated sequence. The set of fixed points is often denoted as Fix(f). There exist a number of fixed-point theorem
Fixed-point theorem
In mathematics, a fixed-point theorem is a result saying that a function F will have at least one fixed point , under some conditions on F that can be stated in general terms...
s that guarantee the existence of fixed points in various situations, including the Banach fixed point theorem
Banach fixed point theorem
In mathematics, the Banach fixed-point theorem is an important tool in the theory of metric spaces; it guarantees the existence and uniqueness of fixed points of certain self-maps of metric spaces, and provides a constructive method to find those fixed points...
and the Brouwer fixed point theorem
Brouwer fixed point theorem
Brouwer's fixed-point theorem is a fixed-point theorem in topology, named after Luitzen Brouwer. It states that for any continuous function f with certain properties there is a point x0 such that f = x0. The simplest form of Brouwer's theorem is for continuous functions f from a disk D to...
.
There are several techniques for convergence acceleration of the sequences produced by fixed point iteration. For example, the Aitken method applied to an iterated fixed point is known as Steffensen's method
Steffensen's method
In numerical analysis, Steffensen's method is a root-finding method, similar to Newton's method, named after Johan Frederik Steffensen. Steffensen's method also achieves quadratic convergence, but without using derivatives as Newton's method does....
, and produces quadratic convergence.
Limiting behaviour
Upon iteration, one may find that there are sets that shrink and converge towards a single point. In such a case, the point that is converged to is known as an attractive fixed point. Conversely, iteration may give the appearance of points diverging away from a single point; this would be the case for an unstable fixed point.When the points of the orbit converge to one or more limits, the set of accumulation points of the orbit is known as the limit set
Limit set
In mathematics, especially in the study of dynamical systems, a limit set is the state a dynamical system reaches after an infinite amount of time has passed, by either going forward or backwards in time...
or the ω-limit set.
The ideas of attraction and repulsion generalize similarly; one may categorize iterates into stable set
Stable manifold
In mathematics, and in particular the study of dynamical systems, the idea of stable and unstable sets or stable and unstable manifolds give a formal mathematical definition to the general notions embodied in the idea of an attractor or repellor...
s and unstable sets, according to the behaviour of small neighborhoods under iteration.
Other limiting behaviours are possible; for example, wandering points are points that move away, and never come back even close to where they started.
Fractional iterates and flows
In some instances, fractional iteration of a function can be defined: for instance, a half iterateFunctional square root
In mathematics, a half iterate is a square root of a function with respect to the operation of function composition. In other words, a functional square root of a function g is a function f satisfying f = g for all x...
of a function f is a function g such that g(g(x)) = f(x). This idea can be generalized so that the iteration count n becomes a continuous parameter; in this case, such a system is called a flow
Flow (mathematics)
In mathematics, a flow formalizes the idea of the motion of particles in a fluid. Flows are ubiquitous in science, including engineering and physics. The notion of flow is basic to the study of ordinary differential equations. Informally, a flow may be viewed as a continuous motion of points over...
, specified by Schröder's equation. (cf. Section on #Conjugacy below.)
Formulae for fractional iteration
One method of finding a series formula for fractional iteration, making use of a fixed point, is as follows.(1) First determine a fixed point for the function such that f(a)=a.
(2) Define
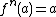for all n belonging to the reals. This in some ways is the most natural extra condition to place upon the fractional iterates.(3) Expand
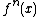around the fixed point a as a Taylor seriesTaylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
.
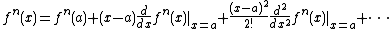
(4) Expand out:
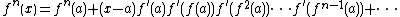
(5) Substitute in for
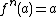:(6) Make use of geometric progression
Geometric progression
In mathematics, a geometric progression, also known as a geometric sequence, is a sequence of numbers where each term after the first is found by multiplying the previous one by a fixed non-zero number called the common ratio. For example, the sequence 2, 6, 18, 54, ... is a geometric progression...
to simplify terms.
(6b) There is a special case when f'(a)=1:
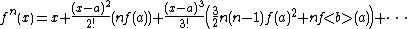
(7) When n is not an integer we make use of the power formula
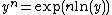
This can be carried on indefinitely although the latter terms become increasingly complicated.
Example 1
For example setting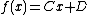 gives the fixed point 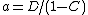and the formula above gives: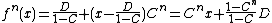which is the correct formula. The next terms are all zero as they contain higher derivatives.
Example 2
We want to find the value of where this is done n times (and perhaps the interpolated values when n is not an integer). We have 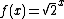. A fixed point is 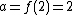. So set x=1 and 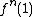expanded around the value of 2 is then an infinite series: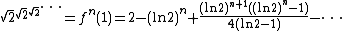which taking just the first three terms is correct to the first decimal place when n is positive. (Using the other fixed point
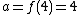causes the series to diverge.)Example 4
With the function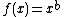 we expand around the fixed point 1 to get the series:-
which is simply the Taylor series of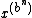
expanded around 1.
Conjugacy
If f and g are two iterated functions, and there exists a homeomorphismHomeomorphismIn the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
h such that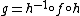
, then f and g are said to be topologically conjugate. Clearly, topological conjugacy is preserved under iteration, as one has that 
, so that if one can solve one iterated function system, one has solutions for all topologically conjugate systems. For example, the tent map is topologically conjugate to the logistic mapLogistic mapThe logistic map is a polynomial mapping of degree 2, often cited as an archetypal example of how complex, chaotic behaviour can arise from very simple non-linear dynamical equations...
.
Even in the absence of a strict homeomorphism, near a fixed point, here taken to be at x=0, f(0)=0, one may often solve Schröder's equation for a function Ψ, which makes f(x) locally conjugate to f (0)x. Thus, its iteration orbit, or flow, under suitable provisions (e.g., f '(0) ≠1), amounts to the conjugate of the orbit of the monomial, Ψ−1(f '(0)n Ψ(x)). Here, however, n no longer needs be integer or positive, and is a continuous "time" of evolution for the full orbit. This is evidently equivalent to the algorithm of the preceding section, albeit more powerful and systematic.
Markov chains
If the function can be described by a stochastic matrixStochastic matrixIn mathematics, a stochastic matrix is a matrix used to describe the transitions of a Markov chain. It has found use in probability theory, statistics and linear algebra, as well as computer science...
, that is, a matrix whose rows or columns sum to one, then the iterated system is known as a Markov chainMarkov chainA Markov chain, named after Andrey Markov, is a mathematical system that undergoes transitions from one state to another, between a finite or countable number of possible states. It is a random process characterized as memoryless: the next state depends only on the current state and not on the...
.
Examples
Famous iterated functions include the Mandelbrot setMandelbrot setThe Mandelbrot set is a particular mathematical set of points, whose boundary generates a distinctive and easily recognisable two-dimensional fractal shape...
and Iterated function systems.
Ernst SchröderErnst SchröderErnst Schröder was a German mathematician mainly known for his work on algebraic logic. He is a major figure in the history of mathematical logic , by virtue of summarizing and extending the work of George Boole, Augustus De Morgan, Hugh MacColl, and especially Charles Peirce...
, in 1870, worked out special cases of the logistic mapLogistic mapThe logistic map is a polynomial mapping of degree 2, often cited as an archetypal example of how complex, chaotic behaviour can arise from very simple non-linear dynamical equations...
, such as the chaotic case f(x) = 4x(1 − x), so that Ψ(x) = arcsin2(√x), hence f n(x) = sin2(2n arcsin(√x)). A nonchaotic case he also illustrated with his method, f(x) = 2x(1 − x), yielded Ψ(x) = −½ ln(1−2x), and hence f n(x) = −½((1−2x)2n−1).
If f is the actionGroup actionIn algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
of a group element on a set, then the iterated function corresponds to a free groupFree groupIn mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
.
Means of study
Iterated functions can be studied with the Artin–Mazur zeta function and with transfer operatorTransfer operatorIn mathematics, the transfer operator encodes information about an iterated map and is frequently used to study the behavior of dynamical systems, statistical mechanics, quantum chaos and fractals...
s.
In computer science
In computer scienceComputer scienceComputer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, iterated functions occur as a special case of recursive functionsRecursion (computer science)Recursion in computer science is a method where the solution to a problem depends on solutions to smaller instances of the same problem. The approach can be applied to many types of problems, and is one of the central ideas of computer science....
, which in turn anchor the study of such broad topics as lambda calculusLambda calculusIn mathematical logic and computer science, lambda calculus, also written as λ-calculus, is a formal system for function definition, function application and recursion. The portion of lambda calculus relevant to computation is now called the untyped lambda calculus...
, or narrower ones, such as the denotational semanticsDenotational semanticsIn computer science, denotational semantics is an approach to formalizing the meanings of programming languages by constructing mathematical objects which describe the meanings of expressions from the languages...
of computer programs.
Definitions in terms of Iterated Functions
Two important functionalsFunctionalGenerally, functional refers to something able to fulfill its purpose or function.*Functionalism and Functional form, movements in architectural design*Functional group, certain atomic combinations that occur in various molecules, e.g...
can be defined in terms of iterated functions. These are SummationSummationSummation is the operation of adding a sequence of numbers; the result is their sum or total. If numbers are added sequentially from left to right, any intermediate result is a partial sum, prefix sum, or running total of the summation. The numbers to be summed may be integers, rational numbers,...
:
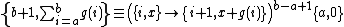
and the equivalent product:
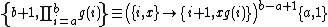
See also
- Irrational rotationIrrational rotationIn mathematical theory of dynamical systems, an irrational rotation is a mapwhere θ is an irrational number. Under the identification of a circle with R/Z, or with the interval [0, 1] with the boundary points glued together, this map becomes a rotation of a circle by a proportion θ of a full...
- Iterated function systemIterated function systemIn mathematics, iterated function systems or IFSs are a method of constructing fractals; the resulting constructions are always self-similar....
- Rotation numberRotation numberIn mathematics, the rotation number is an invariant of homeomorphisms of the circle. It was first defined by Henri Poincaré in 1885, in relation to the precession of the perihelion of a planetary orbit...
- Sarkovskii's theoremSarkovskii's theoremIn mathematics, Sharkovskii's theorem, named after Oleksandr Mikolaiovich Sharkovsky, is a result about discrete dynamical systems. One of the implications of the theorem is that if a continuous discrete dynamical system on the real line has a periodic point of period 3, then it must have...
- Recurrence relationRecurrence relationIn mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms....
- Schröder's equation
- Irrational rotation