Ackermann function
Encyclopedia
In computability theory
, the Ackermann function, named after Wilhelm Ackermann
, is one of the simplest and earliest-discovered examples of a total computable function
that is not primitive recursive
. All primitive recursive functions are total and computable, but the Ackermann function illustrates that not all total computable functions are primitive recursive.
After Ackermann's publication of his function (which had three nonnegative integer arguments), many authors modified it to suit various purposes, so that today "the Ackermann function" may refer to any of numerous variants of the original function. One common version, the two-argument Ackermann–Péter function, is defined as follows for nonnegative integers m and n:
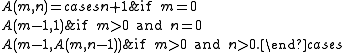
Its value grows rapidly, even for small inputs. For example A(4,2) is an integer of 19,729 decimal digits.
and Wilhelm Ackermann
, students of David Hilbert
, were studying the foundations of computation. Both Sudan and Ackermann are credited with discovering total computable function
s (termed simply "recursive" in some references) that are not primitive recursive
. Sudan published the lesser-known Sudan function
, then shortly afterwards and independently, in 1928, Ackermann published his function
. Ackermann's three-argument function, 
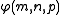, is defined such that for p = 0, 1, 2, it reproduces the basic operations of addition, multiplication, and exponentiation as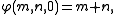
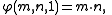
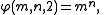
and for p > 2 it extends these basic operations in a way that happens to be expressible in Knuth's up-arrow notation
as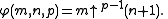
(Aside from its historic role as a total-computable-but-not-primitive-recursive function, Ackermann's original function is seen to extend the basic arithmetic operations beyond exponentiation, although not as seamlessly as do variants of Ackermann's function that are specifically designed for that purpose — such as Goodstein's
hyperoperation
sequence.)
In On the Infinite, David Hilbert hypothesized that the Ackermann function was not primitive recursive, but it was Ackermann, Hilbert’s personal secretary and former student, who actually proved the hypothesis in his paper On Hilbert’s Construction of the Real Numbers. On the Infinite was Hilbert’s most important paper on the foundations of mathematics, serving as the heart of Hilbert's program
to secure the foundation of transfinite number
s by basing them on finite methods.
Rózsa Péter
and Raphael Robinson later developed a two-variable version of the Ackermann function that became preferred by many authors.
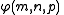is defined recursively
as follows for nonnegative integers m, n, and p:
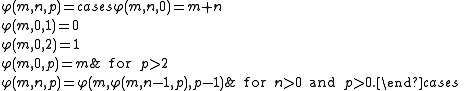
Of the various two-argument versions, the one developed by Péter and Robinson (called "the" Ackermann function by some authors) is defined for nonnegative integers m and n as follows:
It may not be immediately obvious that the evaluation of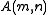
always terminates. However, the recursion is bounded because in each recursive application either m decreases, or m remains the same and n decreases. Each time that n reaches zero, m decreases, so m eventually reaches zero as well. (Expressed more technically, in each case the pair (m, n) decreases in the lexicographic order, which preserves the well-order
ing of the non-negative integers.) However, when m decreases there is no upper bound on how much n can increase — and it will often increase greatly.
The Péter-Ackermann function can also be expressed in terms of various other versions of the Ackermann function:
For small values of m like 1, 2, or 3, the Ackermann function grows relatively slowly with respect to n (at most exponentially
). For m ≥ 4, however, it grows much more quickly; even A(4, 2) is about 2, and the decimal expansion of A(4, 3) is very large by any typical measure.
If we define the function f (n) = A(n, n), which increases both m and n at the same time, we have a function of one variable that dwarfs every primitive recursive function, including very fast-growing functions such as the exponential function
, the factorial function, multi- and superfactorial functions, and even functions defined using Knuth's up-arrow notation (except when the indexed up-arrow is used).
This extreme growth can be exploited to show that f, which is obviously computable on a machine with infinite memory such as a Turing machine
and so is a computable function
, grows faster than any primitive recursive function and is therefore not primitive recursive. In a category with exponentials, using the isomorphism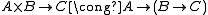
(in computer science, this is called currying
), the Ackermann function may be defined via primitive recursion over higher-order functionals as follows:
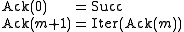
where Succ is the usual successor function and Iter is defined by primitive recursion as well:
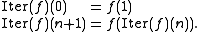
One interesting aspect of the Ackermann function is that the only arithmetic operations it ever uses are addition and subtraction of 1. Its properties come solely from the power of unlimited recursion. This also implies that its running time is at least proportional to its output, and so is also extremely huge. In actuality, for most cases the running time is far larger than the output; see below.
The numbers listed here in a recursive reference are very large and cannot be easily notated in some other form.
Despite the large values occurring in this early section of the table, some even larger numbers have been defined, such as Graham's number
, which cannot be written with any small number of Knuth arrows
. This number is constructed with a technique similar to applying the Ackermann function to itself recursively.
This is a repeat of the above table, but with the values replaced by the relevant expression from the function definition to show the pattern clearly:
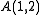in the following way:
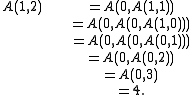
To demonstrate how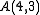
's computation results in many steps and in a large number: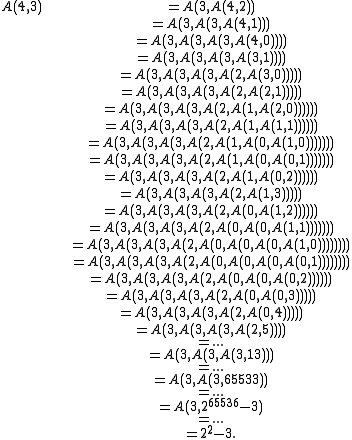
Written as a power of 10, this is roughly equivalent to 106.031.
, f−1, grows very slowly. This inverse Ackermann function f−1 is usually denoted by α. In fact, α(n) is less than 5 for any practical input size n, since A(4, 4) is on the order of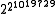
.
This inverse appears in the time complexity
of some algorithm
s, such as the disjoint-set data structure
and Chazelle
's algorithm for minimum spanning tree
s. Sometimes Ackermann's original function or other variations are used in these settings, but they all grow at similarly high rates. In particular, some modified functions simplify the expression by eliminating the −3 and similar terms.
A two-parameter variation of the inverse Ackermann function can be defined as follows, where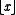
is the floor function
:
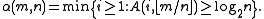
This function arises in more precise analyses of the algorithms mentioned above, and gives a more refined time bound. In the disjoint-set data structure, m represents the number of operations while n represents the number of elements; in the minimum spanning tree algorithm, m represents the number of edges while n represents the number of vertices.
Several slightly different definitions of α(m, n) exist; for example, log2 n is sometimes replaced by n, and the floor function is sometimes replaced by a ceiling.
Other studies might define an inverse function of one where m is set to a constant, such that the inverse applies to a particular row.
's ability to optimize recursion. The first use of Ackermann's function in this way was by Yngve Sundblad, The Ackermann function. A Theoretical, computational and formula manipulative study. (BIT 11 (1971), 107119).
This seminal paper was taken up by Brian Wichmann (co-author of the Whetstone benchmark
) in a trilogy of papers written between 1975 and 1982.
For example, a compiler which, in analyzing the computation of A(3, 30), is able to save intermediate values like A(3, n) and A(2, n) in that calculation rather than recomputing them, can speed up computation of A(3, 30) by a factor of hundreds of thousands. Also, if A(2, n) is computed directly rather than as a recursive expansion of the form A(1, A(1, A(1,...A(1, 0)...))), this will save significant amounts of time. Computing A(1, n) takes linear time in n. Computing A(2, n) requires quadratic time, since it expands to O
(n) nested calls to A(1, i) for various i. Computing A(3, n) requires time proportionate to 4n+1. The computation of A(3, 1) in the example above takes 16 (42) steps.
A(4, 2) cannot possibly be computed by simple recursive application of the Ackermann function in any tractable amount of time. Instead, shortcut formulas such as A(3, n) = 8×2n−3 are used as an optimization to complete some of the recursive calls.
A practical method of computing functions similar to Ackermann's is to use memoization
of intermediate results. A compiler could apply this technique to a function automatically using Donald Michie
's "memo functions".
and Richard K. Guy
define the sequence of Ackermann numbers to be 1↑1, 2↑↑2, 3↑↑↑3, etc.; that is, the n-th Ackermann number is defined to be n↑nn (n = 1, 2, 3, ...), where m↑kn is Knuth's up-arrow
version of the Ackermann function.
The first few Ackermann numbers are:
The fourth Ackermann number, 4↑↑↑↑4, can be written in terms of tetration
towers as follows:
Explanation: in the middle layer, there is a tower of tetration whose full height is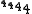
and the final result is the top layer of tetrated 4's whose full height equals the calculation of the middle layer. Note that by way of size comparison, the simple expression 44 already exceeds a googolplex, so the fourth Ackermann number is quite large.
Alternatively, this can be written in terms of exponentiation
towers as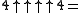
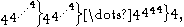
Computability theory
Computability theory, also called recursion theory, is a branch of mathematical logic that originated in the 1930s with the study of computable functions and Turing degrees. The field has grown to include the study of generalized computability and definability...
, the Ackermann function, named after Wilhelm Ackermann
Wilhelm Ackermann
Wilhelm Friedrich Ackermann was a German mathematician best known for the Ackermann function, an important example in the theory of computation....
, is one of the simplest and earliest-discovered examples of a total computable function
Computable function
Computable functions are the basic objects of study in computability theory. Computable functions are the formalized analogue of the intuitive notion of algorithm. They are used to discuss computability without referring to any concrete model of computation such as Turing machines or register...
that is not primitive recursive
Primitive recursive function
The primitive recursive functions are defined using primitive recursion and composition as central operations and are a strict subset of the total µ-recursive functions...
. All primitive recursive functions are total and computable, but the Ackermann function illustrates that not all total computable functions are primitive recursive.
After Ackermann's publication of his function (which had three nonnegative integer arguments), many authors modified it to suit various purposes, so that today "the Ackermann function" may refer to any of numerous variants of the original function. One common version, the two-argument Ackermann–Péter function, is defined as follows for nonnegative integers m and n:
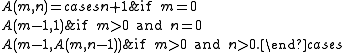
Its value grows rapidly, even for small inputs. For example A(4,2) is an integer of 19,729 decimal digits.
History
In the late 1920s, the mathematicians Gabriel SudanGabriel Sudan
Gabriel Sudan was a Romanian mathematician, known for the Sudan function , an important example in the theory of computation, similar to the Ackermann function .Gabriel Sudan received his Ph.D...
and Wilhelm Ackermann
Wilhelm Ackermann
Wilhelm Friedrich Ackermann was a German mathematician best known for the Ackermann function, an important example in the theory of computation....
, students of David Hilbert
David Hilbert
David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
, were studying the foundations of computation. Both Sudan and Ackermann are credited with discovering total computable function
Computable function
Computable functions are the basic objects of study in computability theory. Computable functions are the formalized analogue of the intuitive notion of algorithm. They are used to discuss computability without referring to any concrete model of computation such as Turing machines or register...
s (termed simply "recursive" in some references) that are not primitive recursive
Primitive recursive function
The primitive recursive functions are defined using primitive recursion and composition as central operations and are a strict subset of the total µ-recursive functions...
. Sudan published the lesser-known Sudan function
Sudan function
In the theory of computation, the Sudan function is an example of a function that is recursive, but not primitive recursive. This is also true of the better-known Ackermann function. The Sudan function was the first function having this property to be published....
, then shortly afterwards and independently, in 1928, Ackermann published his function
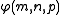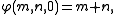
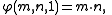
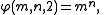
. Ackermann's three-argument function, , is defined such that for p = 0, 1, 2, it reproduces the basic operations of addition, multiplication, and exponentiation asand for p > 2 it extends these basic operations in a way that happens to be expressible in Knuth's up-arrow notation
Knuth's up-arrow notation
In mathematics, Knuth's up-arrow notation is a method of notation for very large integers, introduced by Donald Knuth in 1976. It is closely related to the Ackermann function and especially to the hyperoperation sequence. The idea is based on the fact that multiplication can be viewed as iterated...
as
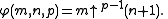
(Aside from its historic role as a total-computable-but-not-primitive-recursive function, Ackermann's original function is seen to extend the basic arithmetic operations beyond exponentiation, although not as seamlessly as do variants of Ackermann's function that are specifically designed for that purpose — such as Goodstein's
Reuben Goodstein
Reuben Louis Goodstein was an English mathematician with a strong interest in the philosophy and teaching of mathematics....
hyperoperation
Hyperoperation
In mathematics, the hyperoperation sequenceis an infinite sequence of arithmetic operations that starts with the unary operation of successor, then continues with the binary operations of addition, multiplication and exponentiation, after which the sequence proceeds with further binary operations...
sequence.)
In On the Infinite, David Hilbert hypothesized that the Ackermann function was not primitive recursive, but it was Ackermann, Hilbert’s personal secretary and former student, who actually proved the hypothesis in his paper On Hilbert’s Construction of the Real Numbers. On the Infinite was Hilbert’s most important paper on the foundations of mathematics, serving as the heart of Hilbert's program
Hilbert's program
In mathematics, Hilbert's program, formulated by German mathematician David Hilbert, was a proposed solution to the foundational crisis of mathematics, when early attempts to clarify the foundations of mathematics were found to suffer from paradoxes and inconsistencies...
to secure the foundation of transfinite number
Transfinite number
Transfinite numbers are numbers that are "infinite" in the sense that they are larger than all finite numbers, yet not necessarily absolutely infinite. The term transfinite was coined by Georg Cantor, who wished to avoid some of the implications of the word infinite in connection with these...
s by basing them on finite methods.
Rózsa Péter
Rózsa Péter
Rózsa Péter , Hungarian name Péter Rózsa, was a Hungarian mathematician. She is best known for her work with recursion theory....
and Raphael Robinson later developed a two-variable version of the Ackermann function that became preferred by many authors.
Definition and properties
Ackermann's original three-argument function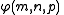 is defined recursivelyRecursion
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
as follows for nonnegative integers m, n, and p:
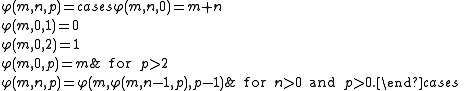
Of the various two-argument versions, the one developed by Péter and Robinson (called "the" Ackermann function by some authors) is defined for nonnegative integers m and n as follows:
It may not be immediately obvious that the evaluation of
always terminates. However, the recursion is bounded because in each recursive application either m decreases, or m remains the same and n decreases. Each time that n reaches zero, m decreases, so m eventually reaches zero as well. (Expressed more technically, in each case the pair (m, n) decreases in the lexicographic order, which preserves the well-orderWell-order
In mathematics, a well-order relation on a set S is a strict total order on S with the property that every non-empty subset of S has a least element in this ordering. Equivalently, a well-ordering is a well-founded strict total order...
ing of the non-negative integers.) However, when m decreases there is no upper bound on how much n can increase — and it will often increase greatly.
The Péter-Ackermann function can also be expressed in terms of various other versions of the Ackermann function:
- the indexed version of Knuth's up-arrow notationKnuth's up-arrow notationIn mathematics, Knuth's up-arrow notation is a method of notation for very large integers, introduced by Donald Knuth in 1976. It is closely related to the Ackermann function and especially to the hyperoperation sequence. The idea is based on the fact that multiplication can be viewed as iterated...
(extended to integer indices ≥ -2):
-
- A(m, n) =
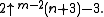
- A(m, n) =
- The part of the definition A(m, 0) = A(m-1, 1) corresponds to
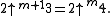
- hyper operators:
-
- A(m, n) = hyper(2, m, n + 3) − 3.
- Conway chained arrow notation:
-
- A(m, n) = (2 → (n+3) → (m − 2)) − 3 for m > 2
- hence
- 2 → n → m = A(m+2,n-3) + 3 for n>2. = −1 and A(m,−1) = 1, which could logically be added.)
For small values of m like 1, 2, or 3, the Ackermann function grows relatively slowly with respect to n (at most exponentially
Exponential growth
Exponential growth occurs when the growth rate of a mathematical function is proportional to the function's current value...
). For m ≥ 4, however, it grows much more quickly; even A(4, 2) is about 2, and the decimal expansion of A(4, 3) is very large by any typical measure.
If we define the function f (n) = A(n, n), which increases both m and n at the same time, we have a function of one variable that dwarfs every primitive recursive function, including very fast-growing functions such as the exponential function
Exponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
, the factorial function, multi- and superfactorial functions, and even functions defined using Knuth's up-arrow notation (except when the indexed up-arrow is used).
This extreme growth can be exploited to show that f, which is obviously computable on a machine with infinite memory such as a Turing machine
Turing machine
A Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a...
and so is a computable function
Computable function
Computable functions are the basic objects of study in computability theory. Computable functions are the formalized analogue of the intuitive notion of algorithm. They are used to discuss computability without referring to any concrete model of computation such as Turing machines or register...
, grows faster than any primitive recursive function and is therefore not primitive recursive. In a category with exponentials, using the isomorphism
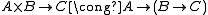(in computer science, this is called curryingCurrying
In mathematics and computer science, currying is the technique of transforming a function that takes multiple arguments in such a way that it can be called as a chain of functions each with a single argument...
), the Ackermann function may be defined via primitive recursion over higher-order functionals as follows:
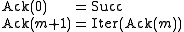
where Succ is the usual successor function and Iter is defined by primitive recursion as well:
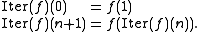
One interesting aspect of the Ackermann function is that the only arithmetic operations it ever uses are addition and subtraction of 1. Its properties come solely from the power of unlimited recursion. This also implies that its running time is at least proportional to its output, and so is also extremely huge. In actuality, for most cases the running time is far larger than the output; see below.
Table of values
Computing the Ackermann function can be restated in terms of an infinite table. We place the natural numbers along the top row. To determine a number in the table, take the number immediately to the left, then look up the required number in the previous row, at the position given by the number just taken. If there is no number to its left, simply look at the column headed "1" in the previous row. Here is a small upper-left portion of the table:| m\n | 0 | 1 | 2 | 3 | 4 | n |
|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 |  |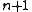
| 1 | 2 | 3 | 4 | 5 | 6 |  |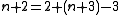
| 2 | 3 | 5 | 7 | 9 | 11 |  |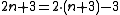
| 3 | 5 | 13 | 29 | 61 | 125 |  |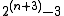
| 4 | 13 =  |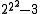
65533 =  |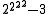
265536 − 3 =  |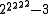
 =  |
 =  |
 |
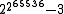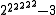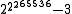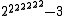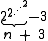The numbers listed here in a recursive reference are very large and cannot be easily notated in some other form.
Despite the large values occurring in this early section of the table, some even larger numbers have been defined, such as Graham's number
Graham's number
Graham's number, named after Ronald Graham, is a large number that is an upper bound on the solution to a certain problem in Ramsey theory.The number gained a degree of popular attention when Martin Gardner described it in the "Mathematical Games" section of Scientific American in November 1977,...
, which cannot be written with any small number of Knuth arrows
Knuth's up-arrow notation
In mathematics, Knuth's up-arrow notation is a method of notation for very large integers, introduced by Donald Knuth in 1976. It is closely related to the Ackermann function and especially to the hyperoperation sequence. The idea is based on the fact that multiplication can be viewed as iterated...
. This number is constructed with a technique similar to applying the Ackermann function to itself recursively.
This is a repeat of the above table, but with the values replaced by the relevant expression from the function definition to show the pattern clearly:
| m\n | 0 | 1 | 2 | 3 | 4 | n |
|---|---|---|---|---|---|---|
| 0 | 0+1 | 1+1 | 2+1 | 3+1 | 4+1 |  |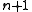
| 1 | A(0,1) | A(0,A(1,0)) | A(0,A(1,1)) | A(0,A(1,2)) | A(0,A(1,3)) |  |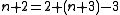
| 2 | A(1,1) | A(1,A(2,0)) | A(1,A(2,1)) | A(1,A(2,2)) | A(1,A(2,3)) |  |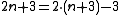
| 3 | A(2,1) | A(2,A(3,0)) | A(2,A(3,1)) | A(2,A(3,2)) | A(2,A(3,3)) |  |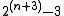
| 4 | A(3,1) | A(3,A(4,0)) | A(3,A(4,1)) | A(3,A(4,2)) | A(3,A(4,3)) |  |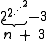
| 5 | A(4,1) | A(4,A(5,0)) | A(4,A(5,1)) | A(4,A(5,2)) | A(4,A(5,3)) | A(4, A(5, n-1)) |
| 6 | A(5,1) | A(5,A(6,0)) | A(5,A(6,1)) | A(5,A(6,2)) | A(5,A(6,3)) | A(5, A(6, n-1)) |
Expansion
To see how the Ackermann function grows so quickly, it helps to expand out some simple expressions using the rules in the original definition. For example, we can fully evaluate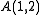 in the following way: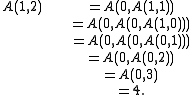To demonstrate how
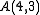's computation results in many steps and in a large number: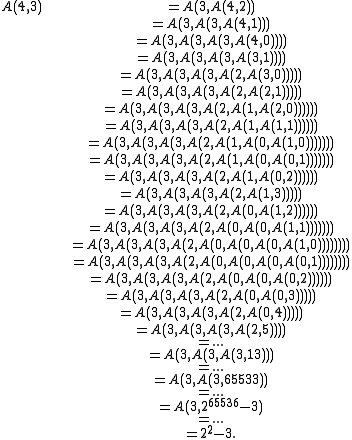Written as a power of 10, this is roughly equivalent to 106.031.
Inverse
Since the function f (n) = A(n, n) considered above grows very rapidly, its inverse functionInverse function
In mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
, f−1, grows very slowly. This inverse Ackermann function f−1 is usually denoted by α. In fact, α(n) is less than 5 for any practical input size n, since A(4, 4) is on the order of
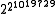.This inverse appears in the time complexity
Computational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
of some algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
s, such as the disjoint-set data structure
Disjoint-set data structure
In computing, a disjoint-set data structure is a data structure that keeps track of a set of elements partitioned into a number of disjoint subsets. A union-find algorithm is an algorithm that performs two useful operations on such a data structure:* Find: Determine which set a particular element...
and Chazelle
Bernard Chazelle
Bernard Chazelle is the Eugene Higgins Professor of Computer Science at Princeton University. Much of his work is in computational geometry, where he has found many of the best-known algorithms, such as linear-time triangulation of a simple polygon, as well as many useful complexity results, such...
's algorithm for minimum spanning tree
Minimum spanning tree
Given a connected, undirected graph, a spanning tree of that graph is a subgraph that is a tree and connects all the vertices together. A single graph can have many different spanning trees...
s. Sometimes Ackermann's original function or other variations are used in these settings, but they all grow at similarly high rates. In particular, some modified functions simplify the expression by eliminating the −3 and similar terms.
A two-parameter variation of the inverse Ackermann function can be defined as follows, where
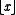is the floor functionFloor function
In mathematics and computer science, the floor and ceiling functions map a real number to the largest previous or the smallest following integer, respectively...
:
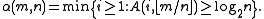
This function arises in more precise analyses of the algorithms mentioned above, and gives a more refined time bound. In the disjoint-set data structure, m represents the number of operations while n represents the number of elements; in the minimum spanning tree algorithm, m represents the number of edges while n represents the number of vertices.
Several slightly different definitions of α(m, n) exist; for example, log2 n is sometimes replaced by n, and the floor function is sometimes replaced by a ceiling.
Other studies might define an inverse function of one where m is set to a constant, such that the inverse applies to a particular row.
Use as benchmark
The Ackermann function, due to its definition in terms of extremely deep recursion, can be used as a benchmark of a compilerCompiler
A compiler is a computer program that transforms source code written in a programming language into another computer language...
's ability to optimize recursion. The first use of Ackermann's function in this way was by Yngve Sundblad, The Ackermann function. A Theoretical, computational and formula manipulative study. (BIT 11 (1971), 107119).
This seminal paper was taken up by Brian Wichmann (co-author of the Whetstone benchmark
Whetstone (benchmark)
The Whetstone benchmark is a synthetic benchmark for evaluating the performance of computers. It was first written in Algol 60 in 1972 at the National Physical Laboratory in the United Kingdom and derived from statistics on program behaviour gathered on the KDF9 computer, using a modified version...
) in a trilogy of papers written between 1975 and 1982.
For example, a compiler which, in analyzing the computation of A(3, 30), is able to save intermediate values like A(3, n) and A(2, n) in that calculation rather than recomputing them, can speed up computation of A(3, 30) by a factor of hundreds of thousands. Also, if A(2, n) is computed directly rather than as a recursive expansion of the form A(1, A(1, A(1,...A(1, 0)...))), this will save significant amounts of time. Computing A(1, n) takes linear time in n. Computing A(2, n) requires quadratic time, since it expands to O
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
(n) nested calls to A(1, i) for various i. Computing A(3, n) requires time proportionate to 4n+1. The computation of A(3, 1) in the example above takes 16 (42) steps.
A(4, 2) cannot possibly be computed by simple recursive application of the Ackermann function in any tractable amount of time. Instead, shortcut formulas such as A(3, n) = 8×2n−3 are used as an optimization to complete some of the recursive calls.
A practical method of computing functions similar to Ackermann's is to use memoization
Memoization
In computing, memoization is an optimization technique used primarily to speed up computer programs by having function calls avoid repeating the calculation of results for previously processed inputs...
of intermediate results. A compiler could apply this technique to a function automatically using Donald Michie
Donald Michie
Donald Michie was a British researcher in artificial intelligence. During World War II, Michie worked for the Government Code and Cypher School at Bletchley Park, contributing to the effort to solve "Tunny," a German teleprinter cipher.-Early life and career:Michie was born in Rangoon, Burma...
's "memo functions".
Ackermann numbers
In The Book of Numbers, John Horton ConwayJohn Horton Conway
John Horton Conway is a prolific mathematician active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory...
and Richard K. Guy
Richard K. Guy
Richard Kenneth Guy is a British mathematician, Professor Emeritus in the Department of Mathematics at the University of Calgary....
define the sequence of Ackermann numbers to be 1↑1, 2↑↑2, 3↑↑↑3, etc.; that is, the n-th Ackermann number is defined to be n↑nn (n = 1, 2, 3, ...), where m↑kn is Knuth's up-arrow
Knuth's up-arrow notation
In mathematics, Knuth's up-arrow notation is a method of notation for very large integers, introduced by Donald Knuth in 1976. It is closely related to the Ackermann function and especially to the hyperoperation sequence. The idea is based on the fact that multiplication can be viewed as iterated...
version of the Ackermann function.
The first few Ackermann numbers are:
- 1↑1 = 11 = 1,
- 2↑↑2 = 2↑2 = 22 = 4,
- 3↑↑↑3 = 3↑↑3↑↑3 = 3↑↑(3↑3↑3) =
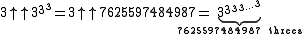
The fourth Ackermann number, 4↑↑↑↑4, can be written in terms of tetration
Tetration
In mathematics, tetration is an iterated exponential and is the next hyper operator after exponentiation. The word tetration was coined by English mathematician Reuben Louis Goodstein from tetra- and iteration. Tetration is used for the notation of very large numbers...
towers as follows:
- 4↑↑↑↑4 = 4↑↑↑4↑↑↑4↑↑↑4 = 4↑↑↑4↑↑↑(4↑↑4↑↑4↑↑4)
-
Explanation: in the middle layer, there is a tower of tetration whose full height is
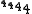and the final result is the top layer of tetrated 4's whose full height equals the calculation of the middle layer. Note that by way of size comparison, the simple expression 44 already exceeds a googolplex, so the fourth Ackermann number is quite large.Alternatively, this can be written in terms of exponentiation
Exponentiation
Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
towers as
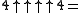
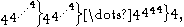
- where the number of towers on the previous line (including the rightmost "4") is
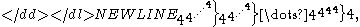
- where the number of towers on the previous line (including the rightmost "4") is
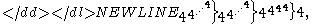
where the number of "4"s in each tower, on each of the lines above, is specified by the value of the next tower to its right (as indicated by a brace).
See also
- Computability theoryComputability theoryComputability theory, also called recursion theory, is a branch of mathematical logic that originated in the 1930s with the study of computable functions and Turing degrees. The field has grown to include the study of generalized computability and definability...
- Recursion (computer science)Recursion (computer science)Recursion in computer science is a method where the solution to a problem depends on solutions to smaller instances of the same problem. The approach can be applied to many types of problems, and is one of the central ideas of computer science....
- Primitive recursive functionPrimitive recursive functionThe primitive recursive functions are defined using primitive recursion and composition as central operations and are a strict subset of the total µ-recursive functions...
- Double recursionDouble recursionIn recursive function theory, double recursion is an extension of primitive recursion which allows the definition of non-primitive recursive functions like the Ackermann function.Raphael M...
External links
- An animated Ackermann function calculator
- Scott AaronsonScott AaronsonScott Joel Aaronson is a theoretical computer scientist and faculty member in the Electrical Engineering and Computer Science department at the Massachusetts Institute of Technology.-Education:...
, Who can name the biggest number? (1999) - Ackermann function's. Includes a table of some values.
- Hyper-operations: Ackermann's Function and New Arithmetical Operation
- Robert Munafo's Large Numbers describes several variations on the definition of A.
- Gabriel Nivasch, Inverse Ackermann without pain on the inverse Ackermann function.
- Raimund Seidel, Understanding the inverse Ackermann function (PDF presentation).
- The Ackermann function written in different programming languages, (on Rosetta CodeRosetta CodeRosetta Code is a wiki-based programming chrestomathy website with solutions to various programming problems in many different programming languages. It was created in 2007 by Mike Mol. Rosetta Code includes 450 programming tasks, and covers 351 programming languages...
) - Ackermann's Function (Archived 2009-10-24) - some study and programming by Harry J. Smith
- Computability theory
- where the number of towers on the previous line (including the rightmost "4") is