
Sequence
Encyclopedia
In mathematics
, a sequence is an ordered list of objects (or events). Like a set, it contains members (also called elements or terms), and the number of terms (possibly infinite) is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence. A sequence is a discrete
function
.
For example, (C, R, Y) is a sequence of letters that differs from (Y, C, R), as the ordering matters. Sequences can be finite, as in this example, or infinite, such as the sequence of all even
positive integer
s (2, 4, 6,...). Finite sequences are sometimes known as strings or words and infinite sequences as streams. The empty sequence ( ) is included in most notions of sequence, but may be excluded depending on the context.
) are not covered by the notations introduced below.
In addition to identifying the elements of a sequence by their position, such as "the 3rd element", elements may be given names for convenient referencing. For example a sequence might be written as (a1, a2, a3, … ), or (b0, b1, b2, … ), or (c0, c2, c4, … ), depending on what is useful in the application.
from {1, 2, ..., n} to S for some n > 0. An infinite sequence in S is a function from {1, 2, ... } to S. For example, the sequence of prime numbers (2,3,5,7,11, … ) is the function 1→2, 2→3, 3→5, 4→7, 5→11, … .
A sequence of a finite length n is also called an n-tuple. Finite sequences include the empty sequence that has no elements.
A function from all integers into a set is sometimes called a bi-infinite sequence or two-way infinite sequence. An example is the bi-infinite sequence of all even integers ( … , -4, -2, 0, 2, 4, 6, 8… ).
The sequence is multiplicative if f(xy) = f(x)f(y) for all x,y such that x and y are coprime
.
of a given sequence is a sequence formed from the given sequence by deleting some of the elements without disturbing the relative positions of the remaining elements.
If the terms of the sequence are a subset of an ordered set
, then a monotonically increasing sequence is one for which each term is greater than or equal to the term before it; if each term is strict
ly greater than the one preceding it, the sequence is called strictly monotonically increasing. A monotonically decreasing sequence is defined similarly. Any sequence fulfilling the monotonicity
property is called monotonic or monotone. This is a special case of the more general notion of monotonic function
.
The terms nondecreasing and nonincreasing are used in order to avoid any possible confusion with strictly increasing and strictly decreasing, respectively.
If the terms of a sequence are integer
s, then the sequence is an integer sequence
. If the terms of a sequence are polynomial
s, then the sequence is a polynomial sequence
.
If S is endowed with a topology
, then it becomes possible to consider convergence of an infinite sequence in S. Such considerations involve the concept of the limit of a sequence
.
If A is a set, the free monoid over A (denoted A*) is a monoid
containing all the finite sequences (or strings) of zero or more elements drawn from A, with the binary operation of concatenation. The free semigroup
A+ is the subsemigroup of A* containing all elements except the empty sequence.
, when talking about sequences, one will generally consider sequences of the form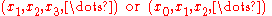
which is to say, infinite sequences of elements indexed by natural number
s.
It may be convenient to have the sequence start with an index different from 1 or 0. For example, the sequence defined by xn = 1/log
(n) would be defined only for n ≥ 2.
When talking about such infinite sequences, it is usually sufficient (and does not change much for most considerations) to assume that the members of the sequence are defined at least for all indices large enough, that is, greater than some given N.
The most elementary type of sequences are numerical ones, that is, sequences of real or complex number
s.
This type can be generalized to sequences of elements of some vector space
. In analysis, the vector spaces considered are often function space
s. Even more generally, one can study sequences with elements in some topological space
.
. More precisely, if (x1, x2, x3, ...) is a sequence, one may consider the sequence of partial sums (S1, S2, S3, ...), with

Formally, this pair of sequences comprises the series with the terms x1, x2, x3, ..., which is denoted as
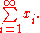
If the sequence of partial sums is convergent, one also uses the infinite sum notation for its limit. For more details, see series
.
(or characters
) drawn from a finite alphabet are of particular interest in theoretical computer science
. They are often referred to simply as sequences or streams, as opposed to finite strings. Infinite binary sequences, for instance, are infinite sequences of bit
s (characters drawn from the alphabet {0,1}). The set C = {0, 1}∞ of all infinite, binary sequences is sometimes called the Cantor space
.
An infinite binary sequence can represent a formal language
(a set of strings) by setting the n th bit of the sequence to 1 if and only if the n th string (in shortlex order
) is in the language. Therefore, the study of complexity class
es, which are sets of languages, may be regarded as studying sets of infinite sequences.
An infinite sequence drawn from the alphabet {0, 1, ..., b−1} may also represent a real number expressed in the base-b positional number system. This equivalence is often used to bring the techniques of real analysis
to bear on complexity classes.
. Specifically, the set of F-valued sequences (where F is a field
) is a function space
(in fact, a product space) of F-valued functions over the set of natural numbers.
In particular, the term sequence space
usually refers to a linear subspace
of the set of all possible infinite sequences with elements in .
.
One can interpret singly infinite sequences as elements of the semigroup ring
of the natural numbers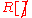 , and doubly infinite sequences as elements of the group ring
, and doubly infinite sequences as elements of the group ring
of the integer
s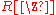 . This perspective is used in the Cauchy product of sequences.
. This perspective is used in the Cauchy product of sequences.
or finite state machine
s can typically be thought of as directed graphs, with edges labeled using some specific alphabet, Σ. Most familiar types of automata transition from state to state by reading input letters from Σ, following edges with matching labels; the ordered input for such an automaton forms a sequence called a word (or input word). The sequence of states encountered by the automaton when processing a word is called a run. A nondeterministic automaton may have unlabeled or duplicate out-edges for any state, giving more than one successor for some input letter. This is typically thought of as producing multiple possible runs for a given word, each being a sequence of single states, rather than producing a single run that is a sequence of sets of states; however, 'run' is occasionally used to mean the latter.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a sequence is an ordered list of objects (or events). Like a set, it contains members (also called elements or terms), and the number of terms (possibly infinite) is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence. A sequence is a discrete
Discrete mathematics
Discrete mathematics is the study of mathematical structures that are fundamentally discrete rather than continuous. In contrast to real numbers that have the property of varying "smoothly", the objects studied in discrete mathematics – such as integers, graphs, and statements in logic – do not...
function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
.
For example, (C, R, Y) is a sequence of letters that differs from (Y, C, R), as the ordering matters. Sequences can be finite, as in this example, or infinite, such as the sequence of all even
Even and odd numbers
In mathematics, the parity of an object states whether it is even or odd.This concept begins with integers. An even number is an integer that is "evenly divisible" by 2, i.e., divisible by 2 without remainder; an odd number is an integer that is not evenly divisible by 2...
positive integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s (2, 4, 6,...). Finite sequences are sometimes known as strings or words and infinite sequences as streams. The empty sequence ( ) is included in most notions of sequence, but may be excluded depending on the context.
Examples and notation
There are various and quite different notions of sequences in mathematics, some of which (e.g., exact sequenceExact sequence
An exact sequence is a concept in mathematics, especially in homological algebra and other applications of abelian category theory, as well as in differential geometry and group theory...
) are not covered by the notations introduced below.
In addition to identifying the elements of a sequence by their position, such as "the 3rd element", elements may be given names for convenient referencing. For example a sequence might be written as (a1, a2, a3, … ), or (b0, b1, b2, … ), or (c0, c2, c4, … ), depending on what is useful in the application.
Finite and infinite
A more formal definition of a finite sequence with terms in a set S is a functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
from {1, 2, ..., n} to S for some n > 0. An infinite sequence in S is a function from {1, 2, ... } to S. For example, the sequence of prime numbers (2,3,5,7,11, … ) is the function 1→2, 2→3, 3→5, 4→7, 5→11, … .
A sequence of a finite length n is also called an n-tuple. Finite sequences include the empty sequence that has no elements.
A function from all integers into a set is sometimes called a bi-infinite sequence or two-way infinite sequence. An example is the bi-infinite sequence of all even integers ( … , -4, -2, 0, 2, 4, 6, 8… ).
Multiplicative
Let A = (a sequence defined by a function f:{1, 2, 3, ...} → {1, 2, 3, ...}, such that a i = f(i).The sequence is multiplicative if f(xy) = f(x)f(y) for all x,y such that x and y are coprime
Coprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
.
Types and properties of sequences
A subsequenceSubsequence
In mathematics, a subsequence is a sequence that can be derived from another sequence by deleting some elements without changing the order of the remaining elements...
of a given sequence is a sequence formed from the given sequence by deleting some of the elements without disturbing the relative positions of the remaining elements.
If the terms of the sequence are a subset of an ordered set
Partially ordered set
In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
, then a monotonically increasing sequence is one for which each term is greater than or equal to the term before it; if each term is strict
Strict
In mathematical writing, the adjective strict is used to modify technical terms which have multiple meanings. It indicates that the exclusive meaning of the term is to be understood. The opposite is non-strict. This is often implicit but can be put explicitly for clarity...
ly greater than the one preceding it, the sequence is called strictly monotonically increasing. A monotonically decreasing sequence is defined similarly. Any sequence fulfilling the monotonicity
Monotonic function
In mathematics, a monotonic function is a function that preserves the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order theory....
property is called monotonic or monotone. This is a special case of the more general notion of monotonic function
Monotonic function
In mathematics, a monotonic function is a function that preserves the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order theory....
.
The terms nondecreasing and nonincreasing are used in order to avoid any possible confusion with strictly increasing and strictly decreasing, respectively.
If the terms of a sequence are integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s, then the sequence is an integer sequence
Integer sequence
In mathematics, an integer sequence is a sequence of integers.An integer sequence may be specified explicitly by giving a formula for its nth term, or implicitly by giving a relationship between its terms...
. If the terms of a sequence are polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s, then the sequence is a polynomial sequence
Polynomial sequence
In mathematics, a polynomial sequence is a sequence of polynomials indexed by the nonnegative integers 0, 1, 2, 3, ..., in which each index is equal to the degree of the corresponding polynomial...
.
If S is endowed with a topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, then it becomes possible to consider convergence of an infinite sequence in S. Such considerations involve the concept of the limit of a sequence
Limit of a sequence
The limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
.
If A is a set, the free monoid over A (denoted A*) is a monoid
Monoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
containing all the finite sequences (or strings) of zero or more elements drawn from A, with the binary operation of concatenation. The free semigroup
Free semigroup
In abstract algebra, the free monoid on a set A is the monoid whose elements are all the finite sequences of zero or more elements from A. It is usually denoted A∗. The identity element is the unique sequence of zero elements, often called the empty string and denoted by ε or λ, and the...
A+ is the subsemigroup of A* containing all elements except the empty sequence.
Sequences in analysis
In analysisMathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, when talking about sequences, one will generally consider sequences of the form
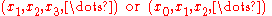
which is to say, infinite sequences of elements indexed by natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s.
It may be convenient to have the sequence start with an index different from 1 or 0. For example, the sequence defined by xn = 1/log
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
(n) would be defined only for n ≥ 2.
When talking about such infinite sequences, it is usually sufficient (and does not change much for most considerations) to assume that the members of the sequence are defined at least for all indices large enough, that is, greater than some given N.
The most elementary type of sequences are numerical ones, that is, sequences of real or complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s.
This type can be generalized to sequences of elements of some vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
. In analysis, the vector spaces considered are often function space
Function space
In mathematics, a function space is a set of functions of a given kind from a set X to a set Y. It is called a space because in many applications it is a topological space, a vector space, or both.-Examples:...
s. Even more generally, one can study sequences with elements in some topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
.
Series
The sum of terms of a sequence is a seriesSeries (mathematics)
A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
. More precisely, if (x1, x2, x3, ...) is a sequence, one may consider the sequence of partial sums (S1, S2, S3, ...), with

Formally, this pair of sequences comprises the series with the terms x1, x2, x3, ..., which is denoted as
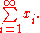
If the sequence of partial sums is convergent, one also uses the infinite sum notation for its limit. For more details, see series
Series (mathematics)
A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
.
Infinite sequences in theoretical computer science
Infinite sequences of digitsNumerical digit
A digit is a symbol used in combinations to represent numbers in positional numeral systems. The name "digit" comes from the fact that the 10 digits of the hands correspond to the 10 symbols of the common base 10 number system, i.e...
(or characters
Character (computing)
In computer and machine-based telecommunications terminology, a character is a unit of information that roughly corresponds to a grapheme, grapheme-like unit, or symbol, such as in an alphabet or syllabary in the written form of a natural language....
) drawn from a finite alphabet are of particular interest in theoretical computer science
Theoretical computer science
Theoretical computer science is a division or subset of general computer science and mathematics which focuses on more abstract or mathematical aspects of computing....
. They are often referred to simply as sequences or streams, as opposed to finite strings. Infinite binary sequences, for instance, are infinite sequences of bit
Bit
A bit is the basic unit of information in computing and telecommunications; it is the amount of information stored by a digital device or other physical system that exists in one of two possible distinct states...
s (characters drawn from the alphabet {0,1}). The set C = {0, 1}∞ of all infinite, binary sequences is sometimes called the Cantor space
Cantor space
In mathematics, a Cantor space, named for Georg Cantor, is a topological abstraction of the classical Cantor set: a topological space is a Cantor space if it is homeomorphic to the Cantor set. In set theory, the topological space 2ω is called "the" Cantor space...
.
An infinite binary sequence can represent a formal language
Formal language
A formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
(a set of strings) by setting the n th bit of the sequence to 1 if and only if the n th string (in shortlex order
Shortlex order
The shortlex order is an ordering for ordered sets of objects, where the sequences are primarily sorted by cardinality with the shortest sequences first, and sequences of the same length are sorted into lexicographical order....
) is in the language. Therefore, the study of complexity class
Complexity class
In computational complexity theory, a complexity class is a set of problems of related resource-based complexity. A typical complexity class has a definition of the form:...
es, which are sets of languages, may be regarded as studying sets of infinite sequences.
An infinite sequence drawn from the alphabet {0, 1, ..., b−1} may also represent a real number expressed in the base-b positional number system. This equivalence is often used to bring the techniques of real analysis
Real analysis
Real analysis, is a branch of mathematical analysis dealing with the set of real numbers and functions of a real variable. In particular, it deals with the analytic properties of real functions and sequences, including convergence and limits of sequences of real numbers, the calculus of the real...
to bear on complexity classes.
Sequences as vectors
Sequences over a field may also be viewed as vectors in a vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
. Specifically, the set of F-valued sequences (where F is a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
) is a function space
Function space
In mathematics, a function space is a set of functions of a given kind from a set X to a set Y. It is called a space because in many applications it is a topological space, a vector space, or both.-Examples:...
(in fact, a product space) of F-valued functions over the set of natural numbers.
In particular, the term sequence space
Sequence space
In functional analysis and related areas of mathematics, a sequence space is a vector space whose elements are infinite sequences of real or complex numbers. Equivalently, it is a function space whose elements are functions from the natural numbers to the field K of real or complex numbers...
usually refers to a linear subspace
Linear subspace
The concept of a linear subspace is important in linear algebra and related fields of mathematics.A linear subspace is usually called simply a subspace when the context serves to distinguish it from other kinds of subspaces....
of the set of all possible infinite sequences with elements in
 .
.Doubly infinite sequences
Normally, the term infinite sequence refers to a sequence which is infinite in one direction, and finite in the other—the sequence has a first element, but no final element (a singly infinite sequence). A doubly infinite sequence is infinite in both directions—it has neither a first nor a final element. Singly infinite sequences are functions from the natural numbers (N) to some set, whereas doubly infinite sequences are functions from the integers (Z) to some set.One can interpret singly infinite sequences as elements of the semigroup ring
Group ring
In algebra, a group ring is a free module and at the same time a ring, constructed in a natural way from any given ring and any given group. As a free module, its ring of scalars is the given ring and its basis is one-to-one with the given group. As a ring, its addition law is that of the free...
of the natural numbers
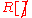 , and doubly infinite sequences as elements of the group ring
, and doubly infinite sequences as elements of the group ringGroup ring
In algebra, a group ring is a free module and at the same time a ring, constructed in a natural way from any given ring and any given group. As a free module, its ring of scalars is the given ring and its basis is one-to-one with the given group. As a ring, its addition law is that of the free...
of the integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s
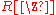 . This perspective is used in the Cauchy product of sequences.
. This perspective is used in the Cauchy product of sequences.Ordinal-indexed sequence
An ordinal-indexed sequence is a generalization of a sequence. If α is a limit ordinal and X is a set, an α-indexed sequence of elements of X is a function from α to X. In this terminology an ω-indexed sequence is an ordinary sequence.Sequences and automata
AutomataAutomata theory
In theoretical computer science, automata theory is the study of abstract machines and the computational problems that can be solved using these machines. These abstract machines are called automata...
or finite state machine
Finite state machine
A finite-state machine or finite-state automaton , or simply a state machine, is a mathematical model used to design computer programs and digital logic circuits. It is conceived as an abstract machine that can be in one of a finite number of states...
s can typically be thought of as directed graphs, with edges labeled using some specific alphabet, Σ. Most familiar types of automata transition from state to state by reading input letters from Σ, following edges with matching labels; the ordered input for such an automaton forms a sequence called a word (or input word). The sequence of states encountered by the automaton when processing a word is called a run. A nondeterministic automaton may have unlabeled or duplicate out-edges for any state, giving more than one successor for some input letter. This is typically thought of as producing multiple possible runs for a given word, each being a sequence of single states, rather than producing a single run that is a sequence of sets of states; however, 'run' is occasionally used to mean the latter.
Types of sequences
- ±1-sequence
- Arithmetic progressionArithmetic progressionIn mathematics, an arithmetic progression or arithmetic sequence is a sequence of numbers such that the difference between the consecutive terms is constant...
- Cauchy sequenceCauchy sequenceIn mathematics, a Cauchy sequence , named after Augustin-Louis Cauchy, is a sequence whose elements become arbitrarily close to each other as the sequence progresses...
- Farey sequenceFarey sequenceIn mathematics, the Farey sequence of order n is the sequence of completely reduced fractions between 0 and 1 which, when in lowest terms, have denominators less than or equal to n, arranged in order of increasing size....
- Fibonacci sequenceFibonacci numberIn mathematics, the Fibonacci numbers are the numbers in the following integer sequence:0,\;1,\;1,\;2,\;3,\;5,\;8,\;13,\;21,\;34,\;55,\;89,\;144,\; \ldots\; ....
- Geometric progressionGeometric progressionIn mathematics, a geometric progression, also known as a geometric sequence, is a sequence of numbers where each term after the first is found by multiplying the previous one by a fixed non-zero number called the common ratio. For example, the sequence 2, 6, 18, 54, ... is a geometric progression...
- Look-and-say sequenceLook-and-say sequenceIn mathematics, the look-and-say sequence is the sequence of integers beginning as follows:To generate a member of the sequence from the previous member, read off the digits of the previous member, counting the number of digits in groups of the same digit...
- Thue–Morse sequenceThue–Morse sequenceIn mathematics, the Thue–Morse sequence, or Prouhet–Thue–Morse sequence, is a binary sequence that begins:Any other ordered pair of symbols may be used instead of 0 and 1; the logical structure of the Thue–Morse sequence does not depend on the symbols that are used to represent it.- Direct...
Related concepts
- List (computing)
- Ordinal-indexed sequence
- Recursion (computer science)Recursion (computer science)Recursion in computer science is a method where the solution to a problem depends on solutions to smaller instances of the same problem. The approach can be applied to many types of problems, and is one of the central ideas of computer science....
- TupleTupleIn mathematics and computer science, a tuple is an ordered list of elements. In set theory, an n-tuple is a sequence of n elements, where n is a positive integer. There is also one 0-tuple, an empty sequence. An n-tuple is defined inductively using the construction of an ordered pair...
- Set theorySet theorySet theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
See also
- Net (topology) (a generalization of sequences)
- On-Line Encyclopedia of Integer SequencesOn-Line Encyclopedia of Integer SequencesThe On-Line Encyclopedia of Integer Sequences , also cited simply as Sloane's, is an online database of integer sequences, created and maintained by N. J. A. Sloane, a researcher at AT&T Labs...
- PermutationPermutationIn mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
- Recurrence relationRecurrence relationIn mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms....
- Sequence spaceSequence spaceIn functional analysis and related areas of mathematics, a sequence space is a vector space whose elements are infinite sequences of real or complex numbers. Equivalently, it is a function space whose elements are functions from the natural numbers to the field K of real or complex numbers...

