
Fractal
Encyclopedia

Shape
The shape of an object located in some space is a geometrical description of the part of that space occupied by the object, as determined by its external boundary – abstracting from location and orientation in space, size, and other properties such as colour, content, and material...
that can be split into parts, each of which is (at least approximately) a reduced-size copy of the whole," a property called self-similarity
Self-similarity
In mathematics, a self-similar object is exactly or approximately similar to a part of itself . Many objects in the real world, such as coastlines, are statistically self-similar: parts of them show the same statistical properties at many scales...
. Roots of the idea of fractals go back to the 17th century, while mathematically rigorous treatment of fractals can be traced back to functions studied by Karl Weierstrass
Karl Weierstrass
Karl Theodor Wilhelm Weierstrass was a German mathematician who is often cited as the "father of modern analysis".- Biography :Weierstrass was born in Ostenfelde, part of Ennigerloh, Province of Westphalia....
, Georg Cantor
Georg Cantor
Georg Ferdinand Ludwig Philipp Cantor was a German mathematician, best known as the inventor of set theory, which has become a fundamental theory in mathematics. Cantor established the importance of one-to-one correspondence between the members of two sets, defined infinite and well-ordered sets,...
and Felix Hausdorff
Felix Hausdorff
Felix Hausdorff was a Jewish German mathematician who is considered to be one of the founders of modern topology and who contributed significantly to set theory, descriptive set theory, measure theory, function theory, and functional analysis.-Life:Hausdorff studied at the University of Leipzig,...
a century later in studying functions that were continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
but not differentiable; however, the term fractal was coined by Benoît Mandelbrot
Benoît Mandelbrot
Benoît B. Mandelbrot was a French American mathematician. Born in Poland, he moved to France with his family when he was a child...
in 1975 and was derived from the Latin
Latin
Latin is an Italic language originally spoken in Latium and Ancient Rome. It, along with most European languages, is a descendant of the ancient Proto-Indo-European language. Although it is considered a dead language, a number of scholars and members of the Christian clergy speak it fluently, and...
frāctus meaning "broken" or "fractured." A mathematical fractal is based on an equation
Equation
An equation is a mathematical statement that asserts the equality of two expressions. In modern notation, this is written by placing the expressions on either side of an equals sign , for examplex + 3 = 5\,asserts that x+3 is equal to 5...
that undergoes iteration
Iteration
Iteration means the act of repeating a process usually with the aim of approaching a desired goal or target or result. Each repetition of the process is also called an "iteration," and the results of one iteration are used as the starting point for the next iteration.-Mathematics:Iteration in...
, a form of feedback
Feedback
Feedback describes the situation when output from an event or phenomenon in the past will influence an occurrence or occurrences of the same Feedback describes the situation when output from (or information about the result of) an event or phenomenon in the past will influence an occurrence or...
based on recursion
Recursion
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
. There are several examples of fractals, which are defined as portraying exact self-similarity, quasi self-similarity, or statistical self-similarity. While fractals are a mathematical construct, they are found in nature, which has led to their inclusion in artwork
Work of art
A work of art, artwork, art piece, or art object is an aesthetic item or artistic creation.The term "a work of art" can apply to:*an example of fine art, such as a painting or sculpture*a fine work of architecture or landscape design...
. They are useful in medicine, soil mechanics
Soil mechanics
Soil mechanics is a branch of engineering mechanics that describes the behavior of soils. It differs from fluid mechanics and solid mechanics in the sense that soils consist of a heterogeneous mixture of fluids and particles but soil may also contain organic solids, liquids, and gasses and other...
, seismology
Seismology
Seismology is the scientific study of earthquakes and the propagation of elastic waves through the Earth or through other planet-like bodies. The field also includes studies of earthquake effects, such as tsunamis as well as diverse seismic sources such as volcanic, tectonic, oceanic,...
, and technical analysis
Technical analysis
In finance, technical analysis is security analysis discipline for forecasting the direction of prices through the study of past market data, primarily price and volume. Behavioral economics and quantitative analysis incorporate technical analysis, which being an aspect of active management stands...
.
Characteristics
A fractal often has the following features:- It has a fine structure at arbitrarily small scales.
- It is too irregular to be easily described in traditional Euclidean geometricEuclidean geometryEuclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
language. - It is self-similar (at least approximately or stochasticStochasticStochastic refers to systems whose behaviour is intrinsically non-deterministic. A stochastic process is one whose behavior is non-deterministic, in that a system's subsequent state is determined both by the process's predictable actions and by a random element. However, according to M. Kac and E...
ally). - It has a Hausdorff dimensionHausdorff dimensionthumb|450px|Estimating the Hausdorff dimension of the coast of Great BritainIn mathematics, the Hausdorff dimension is an extended non-negative real number associated with any metric space. The Hausdorff dimension generalizes the notion of the dimension of a real vector space...
which is greater than its topological dimensionLebesgue covering dimensionLebesgue covering dimension or topological dimension is one of several inequivalent notions of assigning a topological invariant dimension to a given topological space.-Definition:...
(although this requirement is not met by space-filling curveSpace-filling curveIn mathematical analysis, a space-filling curve is a curve whose range contains the entire 2-dimensional unit square...
s such as the Hilbert curveHilbert curveA Hilbert curve is a continuous fractal space-filling curve first described by the German mathematician David Hilbert in 1891, as a variant of the space-filling curves discovered by Giuseppe Peano in 1890....
). - It has a simple and recursive definitionRecursive definitionIn mathematical logic and computer science, a recursive definition is used to define an object in terms of itself ....
.
Because they appear similar at all levels of magnification, fractals are often considered to be infinitely complex (in informal terms). Natural objects that are approximated by fractals to a degree include clouds, mountain ranges, lightning bolts, coastlines, snow flakes, various vegetables (cauliflower and broccoli), and animal coloration patterns. However, not all self-similar objects are fractals—for example, the real line
Real line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
(a straight Euclidean
Line (geometry)
The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
line) is formally self-similar but fails to have other fractal characteristics; for instance, it is regular enough to be described in Euclidean terms.
Images of fractals can be created using fractal-generating software. Images produced by such software are normally referred to as being fractals even if they do not have the above characteristics, such as when it is possible to zoom into a region of the fractal that does not exhibit any fractal properties. Also, these may include calculation or display artifacts
Artifact (error)
In natural science and signal processing, an artifact is any error in the perception or representation of any visual or aural information introduced by the involved equipment or technique....
which are not characteristics of true fractals.
History
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
behind fractals began to take shape in the 17th century when the mathematician and philosopher Gottfried Leibniz
Gottfried Leibniz
Gottfried Wilhelm Leibniz was a German philosopher and mathematician. He wrote in different languages, primarily in Latin , French and German ....
considered recursive
Recursion
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
self-similarity (although he made the mistake of thinking that only the straight line was self-similar in this sense).
It was not until 1872 that a function appeared whose graph
Graph of a function
In mathematics, the graph of a function f is the collection of all ordered pairs . In particular, if x is a real number, graph means the graphical representation of this collection, in the form of a curve on a Cartesian plane, together with Cartesian axes, etc. Graphing on a Cartesian plane is...
would today be considered fractal, when Karl Weierstrass
Karl Weierstrass
Karl Theodor Wilhelm Weierstrass was a German mathematician who is often cited as the "father of modern analysis".- Biography :Weierstrass was born in Ostenfelde, part of Ennigerloh, Province of Westphalia....
gave an example
Weierstrass function
In mathematics, the Weierstrass function is a pathological example of a real-valued function on the real line. The function has the property that it is continuous everywhere but differentiable nowhere...
of a function with the non-intuitive
Intuition (knowledge)
Intuition is the ability to acquire knowledge without inference or the use of reason. "The word 'intuition' comes from the Latin word 'intueri', which is often roughly translated as meaning 'to look inside'’ or 'to contemplate'." Intuition provides us with beliefs that we cannot necessarily justify...
property of being everywhere continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
but nowhere differentiable. In 1904, Helge von Koch
Helge von Koch
Niels Fabian Helge von Koch was a Swedish mathematician who gave his name to the famous fractal known as the Koch snowflake, one of the earliest fractal curves to be described....
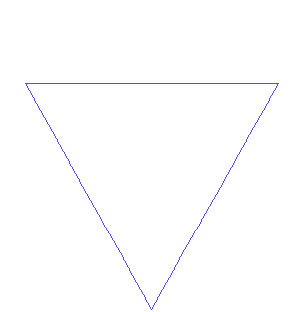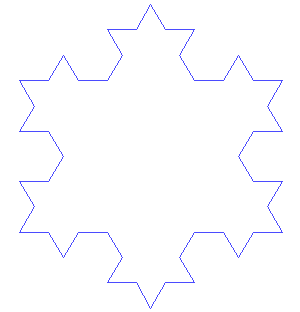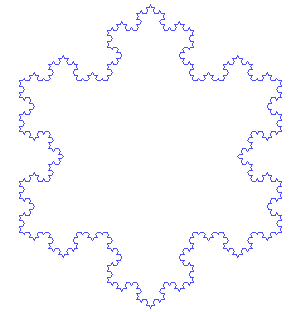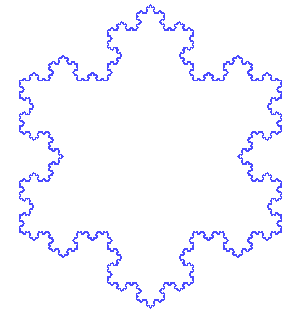
, dissatisfied with Weierstrass's abstract and analytic definition, gave a more geometric definition of a similar function, which is now called the Koch curve. Wacław Sierpiński constructed his triangle
Sierpinski triangle
The Sierpinski triangle , also called the Sierpinski gasket or the Sierpinski Sieve, is a fractal and attractive fixed set named after the Polish mathematician Wacław Sierpiński who described it in 1915. However, similar patterns appear already in the 13th-century Cosmati mosaics in the cathedral...
in 1915 and, one year later, his carpet
Sierpinski carpet
The Sierpinski carpet is a plane fractal first described by Wacław Sierpiński in 1916. The carpet is a generalization of the Cantor set to two dimensions . Sierpiński demonstrated that this fractal is a universal curve, in that any possible one-dimensional graph, projected onto the two-dimensional...
. The idea of self-similar curves was taken further by Paul Pierre Lévy
Paul Pierre Lévy
Paul Pierre Lévy was a Jewish French mathematician who was active especially in probability theory, introducing martingales and Lévy flights...
, who, in his 1938 paper Plane or Space Curves and Surfaces Consisting of Parts Similar to the Whole described a new fractal curve, the Lévy C curve
Lévy C curve
In mathematics, the Lévy C curve is a self-similar fractal that was first described and whose differentiability properties were analysed by Ernesto Cesàro in 1906 and G...
. Georg Cantor
Georg Cantor
Georg Ferdinand Ludwig Philipp Cantor was a German mathematician, best known as the inventor of set theory, which has become a fundamental theory in mathematics. Cantor established the importance of one-to-one correspondence between the members of two sets, defined infinite and well-ordered sets,...
also gave examples of subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
s of the real line with unusual properties—these Cantor set
Cantor set
In mathematics, the Cantor set is a set of points lying on a single line segment that has a number of remarkable and deep properties. It was discovered in 1875 by Henry John Stephen Smith and introduced by German mathematician Georg Cantor in 1883....
s are also now recognized as fractals.
Iterated functions in the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
were investigated in the late 19th and early 20th centuries by Henri Poincaré
Henri Poincaré
Jules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...
, Felix Klein
Felix Klein
Christian Felix Klein was a German mathematician, known for his work in group theory, function theory, non-Euclidean geometry, and on the connections between geometry and group theory...
, Pierre Fatou
Pierre Fatou
Pierre Joseph Louis Fatou was a French mathematician working in the field of complex analytic dynamics. He entered the École Normale Supérieure in Paris in 1898 to study mathematics and graduated in 1901 when he was appointed an astronomy post in the Paris Observatory...
and Gaston Julia
Gaston Julia
Gaston Maurice Julia was a French mathematician who devised the formula for the Julia set. His works were popularized by French mathematician Benoît Mandelbrot; the Julia and Mandelbrot fractals are closely related....
. Without the aid of modern computer graphics, however, they lacked the means to visualize the beauty of many of the objects that they had discovered.
In the 1960s, Benoît Mandelbrot
Benoît Mandelbrot
Benoît B. Mandelbrot was a French American mathematician. Born in Poland, he moved to France with his family when he was a child...
started investigating self-similarity in papers such as How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension
How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension
"How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension" is a paper by mathematician Benoît Mandelbrot, first published in Science in 1967. In this paper Mandelbrot discusses self-similar curves that have Hausdorff dimension between 1 and 2...
, which built on earlier work by Lewis Fry Richardson
Lewis Fry Richardson
Lewis Fry Richardson, FRS was an English mathematician, physicist, meteorologist, psychologist and pacifist who pioneered modern mathematical techniques of weather forecasting, and the application of similar techniques to studying the causes of wars and how to prevent them...
. Finally, in 1975 Mandelbrot coined the word "fractal" to denote an object whose Hausdorff–Besicovitch dimension is greater than its topological dimension. He illustrated this mathematical definition with striking computer-constructed visualizations. These images captured the popular imagination; many of them were based on recursion, leading to the popular meaning of the term "fractal".
.png)
Examples
A class of examples is given by the Cantor setCantor set
In mathematics, the Cantor set is a set of points lying on a single line segment that has a number of remarkable and deep properties. It was discovered in 1875 by Henry John Stephen Smith and introduced by German mathematician Georg Cantor in 1883....
s, Sierpinski triangle
Sierpinski triangle
The Sierpinski triangle , also called the Sierpinski gasket or the Sierpinski Sieve, is a fractal and attractive fixed set named after the Polish mathematician Wacław Sierpiński who described it in 1915. However, similar patterns appear already in the 13th-century Cosmati mosaics in the cathedral...
and carpet
Sierpinski carpet
The Sierpinski carpet is a plane fractal first described by Wacław Sierpiński in 1916. The carpet is a generalization of the Cantor set to two dimensions . Sierpiński demonstrated that this fractal is a universal curve, in that any possible one-dimensional graph, projected onto the two-dimensional...
, Menger sponge
Menger sponge
In mathematics, the Menger sponge is a fractal curve. It is a universal curve, in that it has topological dimension one, and any other curve is homeomorphic to some subset of it. It is sometimes called the Menger-Sierpinski sponge or the Sierpinski sponge...
, dragon curve
Dragon curve
A dragon curve is any member of a family of self-similar fractal curves, which can be approximated by recursive methods such as Lindenmayer systems.-Heighway dragon:...
, space-filling curve
Space-filling curve
In mathematical analysis, a space-filling curve is a curve whose range contains the entire 2-dimensional unit square...
, and Koch curve
Koch snowflake
The Koch snowflake is a mathematical curve and one of the earliest fractal curves to have been described...
. Additional examples of fractals include the Lyapunov fractal
Lyapunov fractal
In mathematics, Lyapunov fractals are bifurcational fractals derived from an extension of the logistic map in which the degree of the growth of the population, r, periodically switches between two values A and B.A Lyapunov fractal is constructed by mapping the regions of stability and chaotic...
and the limit sets of Kleinian group
Kleinian group
In mathematics, a Kleinian group is a discrete subgroup of PSL. The group PSL of 2 by 2 complex matrices of determinant 1 modulo its center has several natural representations: as conformal transformations of the Riemann sphere, and as orientation-preserving isometries of 3-dimensional hyperbolic...
s. Fractals can be deterministic (all the above) or stochastic
Stochastic
Stochastic refers to systems whose behaviour is intrinsically non-deterministic. A stochastic process is one whose behavior is non-deterministic, in that a system's subsequent state is determined both by the process's predictable actions and by a random element. However, according to M. Kac and E...
(that is, non-deterministic). For example, the trajectories of the Brownian motion
Brownian motion
Brownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
in the plane have a Hausdorff dimension of 2.
Chaotic dynamical systems
Chaos theory
Chaos theory is a field of study in mathematics, with applications in several disciplines including physics, economics, biology, and philosophy. Chaos theory studies the behavior of dynamical systems that are highly sensitive to initial conditions, an effect which is popularly referred to as the...
are sometimes associated with fractals. Objects in the phase space
Phase space
In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
of a dynamical system
Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
can be fractals (see attractor
Attractor
An attractor is a set towards which a dynamical system evolves over time. That is, points that get close enough to the attractor remain close even if slightly disturbed...
). Objects in the parameter space
Parameter space
In science, a parameter space is the set of values of parameters encountered in a particular mathematical model. Often the parameters are inputs of a function, in which case the technical term for the parameter space is domain of a function....
for a family of systems may be fractal as well. An interesting example is the Mandelbrot set
Mandelbrot set
The Mandelbrot set is a particular mathematical set of points, whose boundary generates a distinctive and easily recognisable two-dimensional fractal shape...
. This set contains whole discs, so it has a Hausdorff dimension equal to its topological dimension of 2—but what is truly surprising is that the boundary
Boundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
of the Mandelbrot set also has a Hausdorff dimension of 2 (while the topological dimension of 1), a result proved by Mitsuhiro Shishikura
Mitsuhiro Shishikura
is a Japanese mathematician working in the field of complex dynamics. He is currently professor at Kyoto University in Japan.Shishikura became internationally recognized for two of his earliest contributions, both of which solved long-standing open problems....
in 1991. A closely related fractal is the Julia set
Julia set
In the context of complex dynamics, a topic of mathematics, the Julia set and the Fatou set are two complementary sets defined from a function...
.
Generation
Five common techniques for generating fractals are:- Escape-time fractals – (also known as "orbits" fractals) These are defined by a formulaFormulaIn mathematics, a formula is an entity constructed using the symbols and formation rules of a given logical language....
or recurrence relationRecurrence relationIn mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms....
at each point in a space (such as the complex planeComplex planeIn mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
). Examples of this type are the Mandelbrot setMandelbrot setThe Mandelbrot set is a particular mathematical set of points, whose boundary generates a distinctive and easily recognisable two-dimensional fractal shape...
, Julia setJulia setIn the context of complex dynamics, a topic of mathematics, the Julia set and the Fatou set are two complementary sets defined from a function...
, the Burning Ship fractal, the Nova fractalNova fractalNova fractal is a family of fractals related to the Newton fractal. Nova is a formula that is implemented in most fractal art software.-Formula:The formula for novaMandelbrot is a special case of the generalized Newton fractal:...
and the Lyapunov fractalLyapunov fractalIn mathematics, Lyapunov fractals are bifurcational fractals derived from an extension of the logistic map in which the degree of the growth of the population, r, periodically switches between two values A and B.A Lyapunov fractal is constructed by mapping the regions of stability and chaotic...
. The 2d vector fields that are generated by one or two iterations of escape-time formulae also give rise to a fractal form when points (or pixel data) are passed through this field repeatedly. - Iterated function systemIterated function systemIn mathematics, iterated function systems or IFSs are a method of constructing fractals; the resulting constructions are always self-similar....
s – These have a fixed geometric replacement rule. Cantor setCantor setIn mathematics, the Cantor set is a set of points lying on a single line segment that has a number of remarkable and deep properties. It was discovered in 1875 by Henry John Stephen Smith and introduced by German mathematician Georg Cantor in 1883....
, Sierpinski carpetSierpinski carpetThe Sierpinski carpet is a plane fractal first described by Wacław Sierpiński in 1916. The carpet is a generalization of the Cantor set to two dimensions . Sierpiński demonstrated that this fractal is a universal curve, in that any possible one-dimensional graph, projected onto the two-dimensional...
, Sierpinski gasket, Peano curve, Koch snowflakeKoch snowflakeThe Koch snowflake is a mathematical curve and one of the earliest fractal curves to have been described...
, Harter-Heighway dragon curveDragon curveA dragon curve is any member of a family of self-similar fractal curves, which can be approximated by recursive methods such as Lindenmayer systems.-Heighway dragon:...
, T-SquareT-Square (fractal)In mathematics, the T-square is a two-dimensional fractal. As all two-dimensional fractals, it has a boundary of infinite length bounding a finite area...
, Menger spongeMenger spongeIn mathematics, the Menger sponge is a fractal curve. It is a universal curve, in that it has topological dimension one, and any other curve is homeomorphic to some subset of it. It is sometimes called the Menger-Sierpinski sponge or the Sierpinski sponge...
, are some examples of such fractals. - Random fractals – Generated by stochastic rather than deterministic processes, for example, trajectories of the Brownian motionBrownian motionBrownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
, Lévy flightLévy flightA Lévy flight is a random walk in which the step-lengths have a probability distribution that is heavy-tailed. When defined as a walk in a space of dimension greater than one, the steps made are in isotropic random directions...
, percolation clustersPercolation theoryIn mathematics, percolation theory describes the behavior of connected clusters in a random graph. The applications of percolation theory to materials science and other domains are discussed in the article percolation.-Introduction:...
, self avoiding walksSelf-avoiding walkIn mathematics, a self-avoiding walk is a sequence of moves on a lattice that does not visit the same point more than once. A self-avoiding polygon is a closed self-avoiding walk on a lattice...
, fractal landscapes and the Brownian treeBrownian treeA Brownian tree, whose name is derived from Robert Brown via Brownian motion, is a form of computer art that was briefly popular in the 1990s, when home computers started to have sufficient power to simulate Brownian motion...
. The latter yields so-called mass- or dendritic fractals, for example, diffusion-limited aggregationDiffusion-limited aggregationDiffusion-limited aggregation is the process whereby particles undergoing a random walk due to Brownian motion cluster together to form aggregates of such particles. This theory, proposed by Witten and Sander in 1981, is applicable to aggregation in any system where diffusion is the primary means...
or reaction-limited aggregation clusters. - Strange attractorsStrange AttractorsStrange Attractors Audio House is a record label from Portland, Oregon. It was founded in 2000 by Chris Scofield.-History:SAAH was as spin-off of KAOS Olympia 89.3 FM Community Radio's "Strange Attractors" program — a show which Scofield hosted for about eight years...
– Generated by iteration of a map or the solution of a system of initial-value differential equations that exhibit chaos. - L-systemsL-systemAn L-system or Lindenmayer system is a parallel rewriting system, namely a variant of a formal grammar, most famously used to model the growth processes of plant development, but also able to model the morphology of a variety of organisms...
- These are generated by string rewriting and are designed to model the branching patterns of plants.
Fractal-generating programs
There are many fractal generating programs available, both free and commercial. Some of the fractal generating programs include:- Apophysis - open sourceOpen sourceThe term open source describes practices in production and development that promote access to the end product's source materials. Some consider open source a philosophy, others consider it a pragmatic methodology...
software for Microsoft WindowsMicrosoft WindowsMicrosoft Windows is a series of operating systems produced by Microsoft.Microsoft introduced an operating environment named Windows on November 20, 1985 as an add-on to MS-DOS in response to the growing interest in graphical user interfaces . Microsoft Windows came to dominate the world's personal...
based systems - Electric SheepElectric SheepElectric Sheep is a distributed computing project for animating and evolving fractal flames, which are in turn distributed to the networked computers, which display them as a screensaver.-Process:...
- open sourceOpen sourceThe term open source describes practices in production and development that promote access to the end product's source materials. Some consider open source a philosophy, others consider it a pragmatic methodology...
distributed computing software - FractintFractintFractInt is a freeware program that can render and display many kinds of fractals.-Name:Its name comes from the words fractal and integer, since the first versions of it computed fractals by using only integer arithmetic , which led to much faster rendering on x86 computers without math coprocessors...
- freewareFreewareFreeware is computer software that is available for use at no cost or for an optional fee, but usually with one or more restricted usage rights. Freeware is in contrast to commercial software, which is typically sold for profit, but might be distributed for a business or commercial purpose in the...
with available source codeSource codeIn computer science, source code is text written using the format and syntax of the programming language that it is being written in. Such a language is specially designed to facilitate the work of computer programmers, who specify the actions to be performed by a computer mostly by writing source... - Sterling - Freeware software for Microsoft WindowsMicrosoft WindowsMicrosoft Windows is a series of operating systems produced by Microsoft.Microsoft introduced an operating environment named Windows on November 20, 1985 as an add-on to MS-DOS in response to the growing interest in graphical user interfaces . Microsoft Windows came to dominate the world's personal...
based systems - SpangFractSpangFractSpangFract is a fractal-generating program for Mac OS.SpangFract is one of the few deep fractal generators available for the Macintosh platform. The program currently comes with more than 100 available formulas. It is capable of escape, orbit-trap, and "dust" fractals. It features the...
- For Mac OS - Ultra FractalUltra FractalUltra Fractal is a fractal generation and rendering software application. The program works using a similar paradigm to Photoshop, allowing multiple layers to be combined using layer blending modes, transformations and custom fractal formulas....
- A proprietaryProprietary softwareProprietary software is computer software licensed under exclusive legal right of the copyright holder. The licensee is given the right to use the software under certain conditions, while restricted from other uses, such as modification, further distribution, or reverse engineering.Complementary...
fractal generator for Microsoft WindowsMicrosoft WindowsMicrosoft Windows is a series of operating systems produced by Microsoft.Microsoft introduced an operating environment named Windows on November 20, 1985 as an add-on to MS-DOS in response to the growing interest in graphical user interfaces . Microsoft Windows came to dominate the world's personal...
based systems - XaoSXaoSXaoS is an interactive fractal zoomer program. It allows the user to continuously zoom in or out of a fractal in real-time.XaoS is licenced under GPL...
- A cross platform open sourceOpen sourceThe term open source describes practices in production and development that promote access to the end product's source materials. Some consider open source a philosophy, others consider it a pragmatic methodology...
realtime fractal zooming program
Most of the above programs make two-dimensional fractals, with a few creating three-dimensional fractal objects, such as a Quaternion
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
. A specific type of three-dimensional fractal, called mandelbulbs, was introduced in 2009.
Classification
Fractals can also be classified according to their self-similarity. There are three types of self-similarity found in fractals:- Exact self-similarity – This is the strongest type of self-similarity; the fractal appears identical at different scales. Fractals defined by iterated functionIterated functionIn mathematics, an iterated function is a function which is composed with itself, possibly ad infinitum, in a process called iteration. In this process, starting from some initial value, the result of applying a given function is fed again in the function as input, and this process is repeated...
systems often display exact self-similarity. For example, the Sierpinski triangleSierpinski triangleThe Sierpinski triangle , also called the Sierpinski gasket or the Sierpinski Sieve, is a fractal and attractive fixed set named after the Polish mathematician Wacław Sierpiński who described it in 1915. However, similar patterns appear already in the 13th-century Cosmati mosaics in the cathedral...
and Koch snowflakeKoch snowflakeThe Koch snowflake is a mathematical curve and one of the earliest fractal curves to have been described...
exhibit exact self-similarity. - Quasi-self-similarity – This is a looser form of self-similarity; the fractal appears approximately (but not exactly) identical at different scales. Quasi-self-similar fractals contain small copies of the entire fractal in distorted and degenerate forms. Fractals defined by recurrence relationRecurrence relationIn mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms....
s are usually quasi-self-similar. The Mandelbrot setMandelbrot setThe Mandelbrot set is a particular mathematical set of points, whose boundary generates a distinctive and easily recognisable two-dimensional fractal shape...
is quasi-self-similar, as the satellites are approximations of the entire set, but not exact copies. - Statistical self-similarity – This is the weakest type of self-similarity; the fractal has numerical or statistical measures which are preserved across scales. Most reasonable definitions of "fractal" trivially imply some form of statistical self-similarity. (Fractal dimensionFractal dimensionIn fractal geometry, the fractal dimension, D, is a statistical quantity that gives an indication of how completely a fractal appears to fill space, as one zooms down to finer and finer scales. There are many specific definitions of fractal dimension. The most important theoretical fractal...
itself is a numerical measure which is preserved across scales.) Random fractals are examples of fractals which are statistically self-similar. The coastline of Britain is another example; one cannot expect to find microscopic Britains (even distorted ones) by looking at a small section of the coast with a magnifying glass.
Possessing self-similarity is not the sole criterion for an object to be termed a fractal. Examples of self-similar objects that are not fractals include the logarithmic spiral and straight lines, which do contain copies of themselves at increasingly small scales. These do not qualify, since they have the same Hausdorff dimension
Hausdorff dimension
thumb|450px|Estimating the Hausdorff dimension of the coast of Great BritainIn mathematics, the Hausdorff dimension is an extended non-negative real number associated with any metric space. The Hausdorff dimension generalizes the notion of the dimension of a real vector space...
as topological dimension.
In nature
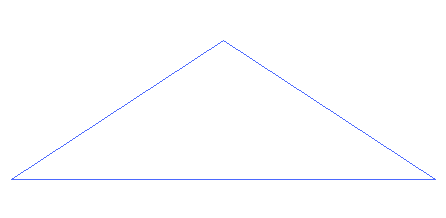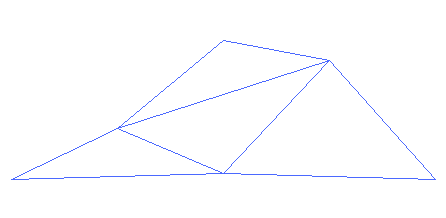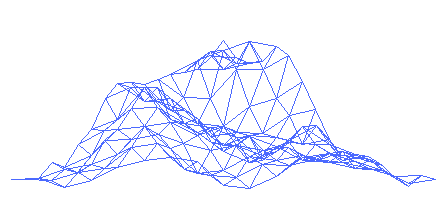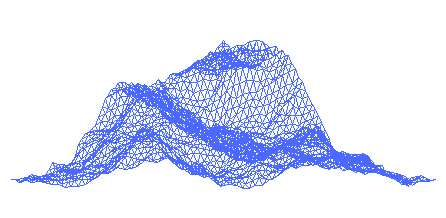
River
A river is a natural watercourse, usually freshwater, flowing towards an ocean, a lake, a sea, or another river. In a few cases, a river simply flows into the ground or dries up completely before reaching another body of water. Small rivers may also be called by several other names, including...
, fault line
Fault line
In geology, fault line refers to the surface trace of a fault.Fault line, Fault Line, or faultline may also refer to:* "Faultline", a song from the 2008 studio album Versus by The Haunted...
s, mountain range
Mountain
Image:Himalaya_annotated.jpg|thumb|right|The Himalayan mountain range with Mount Everestrect 58 14 160 49 Chomo Lonzorect 200 28 335 52 Makalurect 378 24 566 45 Mount Everestrect 188 581 920 656 Tibetan Plateaurect 250 406 340 427 Rong River...
s, craters, snow flakes
Snowflake
Snowflakes are conglomerations of frozen ice crystals which fall through the Earth's atmosphere. They begin as snow crystals which develop when microscopic supercooled cloud droplets freeze. Snowflakes come in a variety of sizes and shapes. Complex shapes emerge as the flake moves through...
, crystal
Crystal
A crystal or crystalline solid is a solid material whose constituent atoms, molecules, or ions are arranged in an orderly repeating pattern extending in all three spatial dimensions. The scientific study of crystals and crystal formation is known as crystallography...
s, lightning
Lightning
Lightning is an atmospheric electrostatic discharge accompanied by thunder, which typically occurs during thunderstorms, and sometimes during volcanic eruptions or dust storms...
, cauliflower
Cauliflower
Cauliflower is one of several vegetables in the species Brassica oleracea, in the family Brassicaceae. It is an annual plant that reproduces by seed...
or broccoli
Broccoli
Broccoli is a plant in the cabbage family, whose large flower head is used as a vegetable.-General:The word broccoli, from the Italian plural of , refers to "the flowering top of a cabbage"....
, and systems of blood vessel
Blood vessel
The blood vessels are the part of the circulatory system that transports blood throughout the body. There are three major types of blood vessels: the arteries, which carry the blood away from the heart; the capillaries, which enable the actual exchange of water and chemicals between the blood and...
s and pulmonary vessels, and ocean waves. DNA
DNA
Deoxyribonucleic acid is a nucleic acid that contains the genetic instructions used in the development and functioning of all known living organisms . The DNA segments that carry this genetic information are called genes, but other DNA sequences have structural purposes, or are involved in...
and heartbeat
Heart sounds
Heart sounds, or heartbeats, are the noises generated by the beating heart and the resultant flow of blood through it...
can be analyzed as fractals. Even coastlines
How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension
"How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension" is a paper by mathematician Benoît Mandelbrot, first published in Science in 1967. In this paper Mandelbrot discusses self-similar curves that have Hausdorff dimension between 1 and 2...
may be loosely considered fractal in nature.
Trees and ferns are fractal in nature and can be modeled on a computer by using a recursive algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
. This recursive nature is obvious in these examples—a branch from a tree or a frond
Frond
The term frond refers to a large, divided leaf. In both common usage and botanical nomenclature, the leaves of ferns are referred to as fronds and some botanists restrict the term to this group...
from a fern is a miniature replica of the whole: not identical, but similar in nature. The connection between fractals and leaves is currently being used to determine how much carbon is contained in trees.
In 1999, certain self similar fractal shapes were shown to have a property of "frequency invariance"—the same electromagnetic properties no matter what the frequency—from Maxwell's equations
Maxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
(see fractal antenna
Fractal antenna
A fractal antenna is an antenna that uses a fractal, self-similar design to maximize the length, or increase the perimeter , of material that can receive or transmit electromagnetic radiation within a given total surface area or volume.Such fractal antennas are also referred to as multilevel and...
).


In creative works
Fractal patterns have been found in the paintings of American artist Jackson PollockJackson Pollock
Paul Jackson Pollock , known as Jackson Pollock, was an influential American painter and a major figure in the abstract expressionist movement. During his lifetime, Pollock enjoyed considerable fame and notoriety. He was regarded as a mostly reclusive artist. He had a volatile personality, and...
. While Pollock's paintings appear to be composed of chaotic dripping and splattering, computer analysis has found fractal patterns in his work.
Decalcomania
Decalcomania
Decalcomania, from the French décalcomanie, is a decorative technique by which engravings and prints may be transferred to pottery or other materials. It was invented in England about 1750 and imported into the United States at least as early as 1865...
, a technique used by artists such as Max Ernst
Max Ernst
Max Ernst was a German painter, sculptor, graphic artist, and poet. A prolific artist, Ernst was one of the primary pioneers of the Dada movement and Surrealism.-Early life:...
, can produce fractal-like patterns. It involves pressing paint between two surfaces and pulling them apart.
Cyberneticist Ron Eglash
Ron Eglash
Ron Eglash is an American cyberneticist, university professor, and author widely known for his work in the field of ethnomathematics, which aims to study the diverse relationships between math and culture...
has suggested that fractal-like structures are prevalent in African art
African art
African art constitutes one of the most diverse legacies on earth. Though many casual observers tend to generalize "traditional" African art, the continent is full of people, societies, and civilizations, each with a unique visual special culture. The definition also includes the art of the African...
and architecture. Circular houses appear in circles of circles, rectangular houses in rectangles of rectangles, and so on. Such scaling patterns can also be found in African textiles, sculpture, and even cornrow hairstyles.
In a 1996 interview with Michael Silverblatt
Michael Silverblatt
Michael Silverblatt is the host of Bookworm, a nationally syndicated radio program about books and literature, originating from Los Angeles public radio station KCRW. A graduate of SUNY Buffalo, Silverblatt created the half-hour interview show in 1989 to share his love of literature, poetry and...
, David Foster Wallace
David Foster Wallace
David Foster Wallace was an American author of novels, essays, and short stories, and a professor at Pomona College in Claremont, California...
admitted that the structure of the first draft of Infinite Jest
Infinite Jest
Infinite Jest is a 1996 novel by David Foster Wallace. The lengthy and complex work takes place in a semi-parodic future version of North America, and touches on tennis, substance addiction and recovery programs, depression, child abuse, family relationships, advertising and popular entertainment,...
he gave to his editor Michael Pietsch was inspired by fractals, specifically the Sierpinski triangle
Sierpinski triangle
The Sierpinski triangle , also called the Sierpinski gasket or the Sierpinski Sieve, is a fractal and attractive fixed set named after the Polish mathematician Wacław Sierpiński who described it in 1915. However, similar patterns appear already in the 13th-century Cosmati mosaics in the cathedral...
(aka Sierpinski gasket) but that the edited novel is "more like a lopsided Sierpinsky Gasket".
Applications
As described above, random fractals have been used to describe/create many highly irregular real-world objects. Other applications of fractals include:- Classification of histopathologyHistopathologyHistopathology refers to the microscopic examination of tissue in order to study the manifestations of disease...
slides in medicineMedicineMedicine is the science and art of healing. It encompasses a variety of health care practices evolved to maintain and restore health by the prevention and treatment of illness.... - Fractal landscapeFractal landscapeA fractal landscape is a surface generated using a stochastic algorithm designed to produce fractal behaviour that mimics the appearance of natural terrain...
or CoastCoastA coastline or seashore is the area where land meets the sea or ocean. A precise line that can be called a coastline cannot be determined due to the dynamic nature of tides. The term "coastal zone" can be used instead, which is a spatial zone where interaction of the sea and land processes occurs...
line complexityComplexityIn general usage, complexity tends to be used to characterize something with many parts in intricate arrangement. The study of these complex linkages is the main goal of complex systems theory. In science there are at this time a number of approaches to characterizing complexity, many of which are... - Enzyme/enzymology (Michaelis-Menten kineticsMichaelis-Menten kineticsIn biochemistry, Michaelis–Menten kinetics is one of the simplest and best-known models of enzyme kinetics. It is named after German biochemist Leonor Michaelis and Canadian physician Maud Menten. The model takes the form of an equation describing the rate of enzymatic reactions, by relating...
) - Generation of new musicAlgorithmic compositionAlgorithmic composition is the technique of using algorithms to create music.Algorithms have been used to compose music for centuries; the procedures used to plot voice-leading in Western counterpoint, for example, can often be reduced to algorithmic determinacy...
- Signal and image compressionFractal compressionFractal compression is a lossy compression method for digital images, based on fractals. The method is best suited for textures and natural images, relying on the fact that parts of an image often resemble other parts of the same image...
- Creation of digital photographic enlargements
- Seismology
- Fractal in soil mechanicsFractal in soil mechanicsThe fractal approach to soil mechanics is a new line of thought. There are several problems in soil mechanics which can be dealt with by applying a fractal approach. One of these problems is the determination of soil-water-characteristic curve...
- Computer and video game designGame designGame design, a subset of game development, is the process of designing the content and rules of a game in the pre-production stage and design of gameplay, environment, storyline, and characters during production stage. The term is also used to describe both the game design embodied in a game as...
, especially computer graphicsComputer graphicsComputer graphics are graphics created using computers and, more generally, the representation and manipulation of image data by a computer with help from specialized software and hardware....
for organicLifeLife is a characteristic that distinguishes objects that have signaling and self-sustaining processes from those that do not, either because such functions have ceased , or else because they lack such functions and are classified as inanimate...
environments and as part of procedural generationProcedural generationProcedural generation is a widely used term in the production of media; it refers to content generated algorithmically rather than manually. Often, this means creating content on the fly rather than prior to distribution... - Fractography and fracture mechanicsFracture mechanicsFracture mechanics is the field of mechanics concerned with the study of the propagation of cracks in materials. It uses methods of analytical solid mechanics to calculate the driving force on a crack and those of experimental solid mechanics to characterize the material's resistance to fracture.In...
- Fractal antennaFractal antennaA fractal antenna is an antenna that uses a fractal, self-similar design to maximize the length, or increase the perimeter , of material that can receive or transmit electromagnetic radiation within a given total surface area or volume.Such fractal antennas are also referred to as multilevel and...
s – Small size antennas using fractal shapes - Small angle scattering theory of fractally rough systemsSAXSSmall-angle scattering is a fundamental method for structure analysis of materials, including biological materials. Small-angle scattering allows one to study the structure of a variety of objects such as solutions of biological macromolecules, nanocomposites, alloys, synthetic polymers, etc...
- T-shirtT-shirtA T-shirt is a style of shirt. A T-shirt is buttonless and collarless, with short sleeves and frequently a round neck line....
s and other fashionFashionFashion, a general term for a currently popular style or practice, especially in clothing, foot wear, or accessories. Fashion references to anything that is the current trend in look and dress up of a person... - Generation of patterns for camouflage, such as MARPATMARPATMARPAT is a digital camouflage pattern in use with the United States Marine Corps, introduced with the Marine Corps Combat Utility Uniform , which replaced the Camouflage Utility Uniform. The pattern is formed by a number of small rectangular pixels of color...
- Digital sundialDigital sundialA digital sundial is a clock that indicates the current time with numerals formed by the sunlight striking it. Like a classical sundial, the device is purely passive and contains no moving parts. It uses no electricity nor other artificial sources of energy....
- Technical analysis of price series (see Elliott wave principleElliott wave principleThe Elliott Wave Principle is a form of technical analysis that some traders use to analyze financial market cycles and forecast market trends by identifying extremes in investor psychology, highs and lows in prices, and other collective factors...
) - Fractals in networksFractal dimension on networks-Self-similarity of complex networks:Many real networks have two fundamental properties, scale-free property and small-world property. If the degree distribution of the network follows a power-law, the network is scale-free; if any two arbitrary nodes in a network can be connected in a very small...
See also
- Banach fixed point theoremBanach fixed point theoremIn mathematics, the Banach fixed-point theorem is an important tool in the theory of metric spaces; it guarantees the existence and uniqueness of fixed points of certain self-maps of metric spaces, and provides a constructive method to find those fixed points...
- Bifurcation theoryBifurcation theoryBifurcation theory is the mathematical study of changes in the qualitative or topological structure of a given family, such as the integral curves of a family of vector fields, and the solutions of a family of differential equations...
- Butterfly effectButterfly effectIn chaos theory, the butterfly effect is the sensitive dependence on initial conditions; where a small change at one place in a nonlinear system can result in large differences to a later state...
- ComplexityComplexityIn general usage, complexity tends to be used to characterize something with many parts in intricate arrangement. The study of these complex linkages is the main goal of complex systems theory. In science there are at this time a number of approaches to characterizing complexity, many of which are...
- Constructal theoryConstructal theoryThe constructal law puts forth the idea that the generation of design in nature is a physics phenomenon that unites all animate and inanimate systems, and that this phenomenon is covered by the Constructal Law...
- CymaticsCymaticsCymatics is the study of visible sound and vibration, a subset of modal phenomena. Typically the surface of a plate, diaphragm, or membrane is vibrated, and regions of maximum and minimum displacement are made visible in a thin coating of particles, paste, or liquid...
- Diamond-square algorithmDiamond-square algorithmThe diamond-square algorithm is a method for generating highly realistic heightmaps for computer graphics. It is a slightly better algorithm than the three-dimensional implementation of the midpoint displacement algorithm which produces two-dimensional landscapes...
- Droste effectDroste effectThe Droste effect is a specific kind of recursive picture, one that in heraldry is termed mise en abyme. An image exhibiting the Droste effect depicts a smaller version of itself in a place where a similar picture would realistically be expected to appear. This smaller version then depicts an even...
- Feigenbaum functionFeigenbaum functionIn the study of dynamical systems the term Feigenbaum function has been used to describe two different functions introduced by the physicist Mitchell Feigenbaum:* the solution to the Feigenbaum-Cvitanović functional equation; and...
- Fractal compressionFractal compressionFractal compression is a lossy compression method for digital images, based on fractals. The method is best suited for textures and natural images, relying on the fact that parts of an image often resemble other parts of the same image...
- Fractal cosmologyFractal cosmologyIn physical cosmology, fractal cosmology is a set of minority cosmological theories which state that the distribution of matter in the Universe, or the structure of the universe itself, is a fractal. More generally, it relates to the usage or appearance of fractals in the study of the universe and...
- Fractal networksFractal dimension on networks-Self-similarity of complex networks:Many real networks have two fundamental properties, scale-free property and small-world property. If the degree distribution of the network follows a power-law, the network is scale-free; if any two arbitrary nodes in a network can be connected in a very small...
- FractintFractintFractInt is a freeware program that can render and display many kinds of fractals.-Name:Its name comes from the words fractal and integer, since the first versions of it computed fractals by using only integer arithmetic , which led to much faster rendering on x86 computers without math coprocessors...
- FractonFractonA fracton is a collective quantized vibration on a substrate with a fractal structure.Fractons are the fractal analog of phonons. Phonons are the result of applying translational symmetry to the potential in a Schrödinger equation. Fractal self-similarity can be thought of as a symmetry somewhat...
- Golden ratioGolden ratioIn mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
- Graftal
- GreebleGreebleA greeble or nurnie is a small piece of detailing added to break up the surface of an object to add visual interest to a surface or object, particularly in movie special effects. They serve no real purpose other than to add complexity to the object, and cause the flow of the eye over the surface of...
- LacunarityLacunarityIn geometry, lacunarity is a measure of how a fractal fills space. It is used to further classify fractals and textures which, while sharing the same fractal dimension, appear very visually different....
- List of fractals by Hausdorff dimension
- Publications in fractal geometry
- MandelbulbMandelbulbThe Mandelbulb is a three-dimensional analogue of the Mandelbrot set, constructed by Daniel White and Paul Nylander using spherical coordinates....
- Multifractal systemMultifractal systemA multifractal system is a generalization of a fractal system in which a single exponent is not enough to describe its dynamics; instead, a continuous spectrum of exponents is needed....
- Newton fractal
- PercolationPercolationIn physics, chemistry and materials science, percolation concerns the movement and filtering of fluids through porous materials...
- Power lawPower lawA power law is a special kind of mathematical relationship between two quantities. When the frequency of an event varies as a power of some attribute of that event , the frequency is said to follow a power law. For instance, the number of cities having a certain population size is found to vary...
- Random walkRandom walkA random walk, sometimes denoted RW, is a mathematical formalisation of a trajectory that consists of taking successive random steps. For example, the path traced by a molecule as it travels in a liquid or a gas, the search path of a foraging animal, the price of a fluctuating stock and the...
- Sacred geometrySacred geometrySacred geometry is the geometry used in the planning and construction of religious structures such as churches, temples, mosques, religious monuments, altars, tabernacles; as well as for sacred spaces such as temenoi, sacred groves, village greens and holy wells, and the creation of religious art...
- Self avoiding walk
- Self-referenceSelf-referenceSelf-reference occurs in natural or formal languages when a sentence or formula refers to itself. The reference may be expressed either directly—through some intermediate sentence or formula—or by means of some encoding...
- Strange loopStrange loopA strange loop arises when, by moving up or down through a hierarchical system, one finds oneself back where one started.Strange loops may involve self-reference and paradox...
- TurbulenceTurbulenceIn fluid dynamics, turbulence or turbulent flow is a flow regime characterized by chaotic and stochastic property changes. This includes low momentum diffusion, high momentum convection, and rapid variation of pressure and velocity in space and time...
External links
- Scaling and Fractals presented by Shlomo HavlinShlomo HavlinShlomo Havlin is a Professor in the Department of Physics at Bar-Ilan University, Ramat-Gan, Israel. He served as President of the Israel Physical Society , Dean of Faculty of Exact Sciences , Chairman, Department of Physics .-Biography:Professor Shlomo Havlin was born in Jerusalem, Israel...
, Bar-Ilan UniversityBar-Ilan UniversityBar-Ilan University is a university in Ramat Gan of the Tel Aviv District, Israel.Established in 1955, Bar Ilan is now Israel's second-largest academic institution. It has nearly 26,800 students and 1,350 faculty members... - Hunting the Hidden Dimension, PBS NOVANOVA (TV series)Nova is a popular science television series from the U.S. produced by WGBH Boston. It can be seen on the Public Broadcasting Service in the United States, and in more than 100 other countries...
, first aired August 24, 2011

