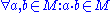.gif)
Magma (algebra)
Encyclopedia
In abstract algebra
, a magma (or groupoid; not to be confused with groupoid
s in category theory
) is a basic kind of algebraic structure
. Specifically, a magma consists of a set
equipped with a single binary operation
.
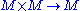A binary operation is closed by definition, but no other axiom
s are imposed on the operation.
The term magma for this kind of structure was introduced by Nicolas Bourbaki
. The term groupoid is an older, but still commonly used alternative which was introduced by Øystein Ore
.
matched with an operation
"
" that sends any two elements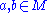 
to another element 
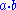. The symbol "
" is a general placeholder for a properly defined operation. To qualify as a magma, the set and operation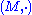 
must satisfy the following requirement (known as the magma axiom):
And in mathematical notation:
Commonly studied types of magmas include
of magmas is a function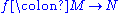
mapping magma 
to magma 
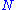, that preserves the binary operation:
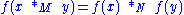
where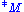
and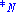 
denote the binary operation on 
and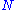 
respectively.
consists of symbols denoting elements of the magma, and balanced sets of parenthesis. The set of all possible strings of balanced parenthesis is called the Dyck language
. The total number of different ways of writing
applications of the magma operator is given by the Catalan number
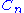. Thus, for example, 
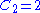, which is just the statement that 
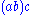and 
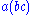are the only two ways of pairing three elements of a magma with two operations.
A shorthand is often used to reduce the number of parentheses. This is accomplished by using juxtaposition in place of the operation. For example, if the magma operation is
, then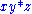 
abbreviates 
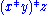. Further abbreviations are possible by inserting spaces, for example by writing 
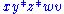in place of 
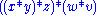. Of course, for more complex expressions the use of parenthesis turns out to be inevitable. A way to avoid completely the use of parentheses is prefix notation.
on a set 
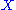is the "most general possible" magma generated by the set 
(that is there are no relations or axioms imposed on the generators; see free object
). It can be described, in terms familiar in computer science
, as the magma of binary tree
s with leaves labeled by elements of
. The operation is that of joining trees at the root. It therefore has a foundational role in syntax
.
A free magma has the universal property
such that, if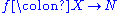
is a function from the set 
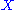to any magma 
, then there is a unique extension of 
to a morphism of magmas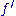 
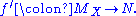
See also: free semigroup
, free group
, Hall set
If
is instead a partial operation, then S is called a partial magma.
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, a magma (or groupoid; not to be confused with groupoid
Groupoid
In mathematics, especially in category theory and homotopy theory, a groupoid generalises the notion of group in several equivalent ways. A groupoid can be seen as a:...
s in category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
) is a basic kind of algebraic structure
Algebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
. Specifically, a magma consists of a set
equipped with a single binary operationBinary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
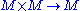.A binary operation is closed by definition, but no other axiom
Axiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
s are imposed on the operation.
The term magma for this kind of structure was introduced by Nicolas Bourbaki
Nicolas Bourbaki
Nicolas Bourbaki is the collective pseudonym under which a group of 20th-century mathematicians wrote a series of books presenting an exposition of modern advanced mathematics, beginning in 1935. With the goal of founding all of mathematics on set theory, the group strove for rigour and generality...
. The term groupoid is an older, but still commonly used alternative which was introduced by Øystein Ore
Øystein Ore
Øystein Ore was a Norwegian mathematician.-Life:Ore was graduated from the University of Oslo in 1922, with a Cand.Scient. degree in mathematics. In 1924, the University of Oslo awarded him the Ph.D. for a thesis titled Zur Theorie der algebraischen Körper, supervised by Thoralf Skolem...
.
Definition
A magma is a set matched with an operationBinary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
"
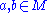" that sends any two elements to another element 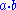. The symbol "" is a general placeholder for a properly defined operation. To qualify as a magma, the set and operation 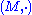must satisfy the following requirement (known as the magma axiom):- For all
, 
in 
, the result of the operation 
is also in 
.
And in mathematical notation:
Etymology
In French, the word "magma" has multiple common meanings, one of them being "jumble". It is likely that the French Bourbaki group referred to sets with well-defined binary operations as magmas with the "jumble" definition in mind.Types of magmas
Magmas are not often studied as such; instead there are several different kinds of magmas, depending on what axioms one might require of the operation.Commonly studied types of magmas include
- quasigroupQuasigroupIn mathematics, especially in abstract algebra, a quasigroup is an algebraic structure resembling a group in the sense that "division" is always possible...
s—nonempty magmas where divisionDivision (mathematics)right|thumb|200px|20 \div 4=5In mathematics, especially in elementary arithmetic, division is an arithmetic operation.Specifically, if c times b equals a, written:c \times b = a\,...
is always possible; - loops—quasigroups with identity elementIdentity elementIn mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
s; - semigroupSemigroupIn mathematics, a semigroup is an algebraic structure consisting of a set together with an associative binary operation. A semigroup generalizes a monoid in that there might not exist an identity element...
s—magmas where the operation is associative; - monoidMonoidIn abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
s—semigroups with identity elementIdentity elementIn mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
s; - groupGroup (mathematics)In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
s—monoids with inverse elementInverse elementIn abstract algebra, the idea of an inverse element generalises the concept of a negation, in relation to addition, and a reciprocal, in relation to multiplication. The intuition is of an element that can 'undo' the effect of combination with another given element...
s, or equivalently, associative loops or associative quasigroups; - abelian groupAbelian groupIn abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s—groups where the operation is commutative.
-
- Note that both divisibility and invertibility imply
- the existence of the cancellation propertyCancellation propertyIn mathematics, the notion of cancellative is a generalization of the notion of invertible.An element a in a magma has the left cancellation property if for all b and c in M, a * b = a * c always implies b = c.An element a in a magma has the right cancellation...
.
Morphism of magmas
A morphismMorphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
of magmas is a function
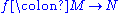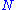mapping magma to magma , that preserves the binary operation: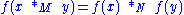where
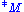and 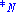denote the binary operation on and 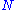respectively.Combinatorics and parentheses
For the general, non-associative case, the magma operation may be repeatedly iterated. To denote pairings, parentheses are used. The resulting stringString (computer science)
In formal languages, which are used in mathematical logic and theoretical computer science, a string is a finite sequence of symbols that are chosen from a set or alphabet....
consists of symbols denoting elements of the magma, and balanced sets of parenthesis. The set of all possible strings of balanced parenthesis is called the Dyck language
Dyck language
In the theory of formal languages of computer science, mathematics, and linguistics, the Dyck language is the language consisting of balanced strings of parentheses [ and ]. It is important in the parsing of expressions that must have a correctly nested sequence of parentheses, such as arithmetic...
. The total number of different ways of writing
applications of the magma operator is given by the Catalan numberCatalan number
In combinatorial mathematics, the Catalan numbers form a sequence of natural numbers that occur in various counting problems, often involvingrecursively defined objects...
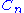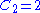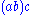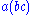. Thus, for example, , which is just the statement that and are the only two ways of pairing three elements of a magma with two operations.A shorthand is often used to reduce the number of parentheses. This is accomplished by using juxtaposition in place of the operation. For example, if the magma operation is
, then 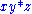abbreviates 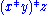. Further abbreviations are possible by inserting spaces, for example by writing 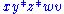in place of 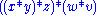. Of course, for more complex expressions the use of parenthesis turns out to be inevitable. A way to avoid completely the use of parentheses is prefix notation.Free magma
A free magma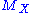 on a set 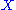is the "most general possible" magma generated by the set (that is there are no relations or axioms imposed on the generators; see free objectFree object
In mathematics, the idea of a free object is one of the basic concepts of abstract algebra. It is a part of universal algebra, in the sense that it relates to all types of algebraic structure . It also has a formulation in terms of category theory, although this is in yet more abstract terms....
). It can be described, in terms familiar in computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, as the magma of binary tree
Binary tree
In computer science, a binary tree is a tree data structure in which each node has at most two child nodes, usually distinguished as "left" and "right". Nodes with children are parent nodes, and child nodes may contain references to their parents. Outside the tree, there is often a reference to...
s with leaves labeled by elements of
. The operation is that of joining trees at the root. It therefore has a foundational role in syntaxSyntax
In linguistics, syntax is the study of the principles and rules for constructing phrases and sentences in natural languages....
.
A free magma has the universal property
Universal property
In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
such that, if
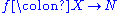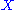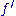
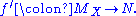
is a function from the set to any magma , then there is a unique extension of to a morphism of magmas See also: free semigroup
Free semigroup
In abstract algebra, the free monoid on a set A is the monoid whose elements are all the finite sequences of zero or more elements from A. It is usually denoted A∗. The identity element is the unique sequence of zero elements, often called the empty string and denoted by ε or λ, and the...
, free group
Free group
In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
, Hall set
Classification by properties
A magma (S, *) is called- unital if it has an identity element,
- medialMedial- Medial magmas :In abstract algebra, a medial magma is a set with a binary operation which satisfies the identity \cdot = \cdot , or more simply, xy\cdot uv = xu\cdot yv...
if it satisfies the identity xy * uz = xu * yz (i.e. (x * y) * (u * z) = (x * u) * (y * z) for all x, y, u, z in S), - left semimedial if it satisfies the identity xx * yz = xy * xz,
- right semimedial if it satisfies the identity yz * xx = yx * zx,
- semimedial if it is both left and right semimedial,
- left distributive if it satisfies the identity x * yz = xy * xz,
- right distributive if it satisfies the identity yz * x = yx * zx,
- autodistributive if it is both left and right distributive,
- commutative if it satisfies the identity xy = yx,
- idempotent if it satisfies the identity xx = x,
- unipotentUnipotentIn mathematics, a unipotent element r of a ring R is one such that r − 1 is a nilpotent element, in other words such that some power n is zero....
if it satisfies the identity xx = yy, - zeropotent if it satisfies the identity xx * y = yy * x = xx,
- alternativeAlternativityIn abstract algebra, alternativity is a property of a binary operation. A magma G is said to be left alternative if y = x for all x and y in G and right alternative if y = x for all x and y in G...
if it satisfies the identities xx * y = x * xy and x * yy = xy * y, - power-associative if the submagma generated by any element is associative,
- left-cancellative if for all x, y, and z, xy = xz implies y = z
- right-cancellative if for all x, y, and z, yx = zx implies y = z
- cancellative if it is both right-cancellative and left-cancellative
- a semigroupSemigroupIn mathematics, a semigroup is an algebraic structure consisting of a set together with an associative binary operation. A semigroup generalizes a monoid in that there might not exist an identity element...
if it satisfies the identity x * yz = xy * z (associativity), - a semigroup with left zeros if there are elements x for which the identity x = xy holds,
- a semigroup with right zeros if there are elements x for which the identity x = yx holds,
- a semigroup with zero multiplication or a null semigroupNull semigroupIn mathematics, a null semigroup is a semigroup with an absorbing element, called zero, in which the product of any two elements is zero...
if it satisfies the identity xy = uv, for all x,y,u and v - a left unar if it satisfies the identity xy = xz,
- a right unar if it satisfies the identity yx = zx,
- trimedial if any triple of its (not necessarily distinct) elements generates a medial submagma,
- entropic if it is a homomorphic imageUniversal algebraUniversal algebra is the field of mathematics that studies algebraic structures themselves, not examples of algebraic structures....
of a medial cancellation magma.
If
is instead a partial operation, then S is called a partial magma.See also
- Magma category
- Auto magma objectAuto magma objectIn mathematics, a magma in a category, or magma object, can be defined in a category with a cartesian product. This is the 'internal' form of definition of a binary operation in a category....
- Universal algebraUniversal algebraUniversal algebra is the field of mathematics that studies algebraic structures themselves, not examples of algebraic structures....
- Magma computer algebra systemMagma computer algebra systemMagma is a computer algebra system designed to solve problems in algebra, number theory, geometry and combinatorics. It is named after the algebraic structure magma...
, named after the object of this article. - An example of a commutative non-associative magmaExample of a commutative non-associative magmaIn mathematics, it can be shown that there exist magmas that are commutative but not associative. A simple example of such a magma is given by considering the children's game of rock, paper, scissors.-A commutative non-associative magma:...
- Algebraic structures whose axioms are all identities