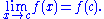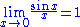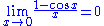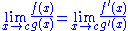
Limit of a function
Encyclopedia
In mathematics
, the limit of a function is a fundamental concept in calculus
and analysis
concerning the behavior of that function
near a particular input
.
Formal definitions, first devised in the early 19th century, are given below. Informally, a function f assigns an output f(x) to every input x. The function has a limit L at an input p if f(x) is "close" to L whenever x is "close" to p. In other words, f(x) becomes closer and closer to L as x moves closer and closer to p. More specifically, when f is applied to each input sufficiently close to p, the result is an output value that is arbitrarily close to L. If the inputs "close" to p are taken to values that are very different, the limit is said to not exist.
The notion of a limit has many applications in modern calculus. In particular, the many definitions of continuity
employ the limit: roughly, a function is continuous if all of its limits agree with the values of the function. It also appears in the definition of the derivative
: in the calculus of one variable, this is the limiting value of the slope of secant lines to the graph of a function.
who, in 1817, introduced the basics of the epsilon-delta technique to define continuous functions. However, his work was not known during his lifetime . Cauchy discussed limits in his Cours d'analyse (1821) and gave essentially the modern definition, but this is not often recognized because he only gave a verbal definition . Weierstrass first introduced the epsilon-delta definition of limit in the form it is usually written today. He also introduced the notations lim and limx→x0 .
The modern notation of placing the arrow below the limit symbol is due to Hardy
in his book A Course of Pure Mathematics in 1908 .
What, then, does it mean to say that his altitude approaches L? It means that his altitude gets nearer and nearer to L except for a possible small error in accuracy. For example, suppose a particular accuracy goal is set for our traveler: he must get within ten meters of L in altitude. He reports back that indeed he can get within ten meters of L, since he notes that when he is anywhere within fifty horizontal meters of p, his altitude is always ten meters or less from L.
The accuracy goal is then changed: can he get within one vertical meter? Yes. If he is anywhere within seven horizontal meters of p, then his altitude always remains within one meter from the target L. In summary, to say that the traveler's altitude approaches L as his horizontal position approaches p means that for every target accuracy goal, however small it may be, there is some neighborhood of p whose altitude fulfills that accuracy goal.
The initial informal statement can now be explicated:
This explicit statement is quite close to the formal definition of the limit of a function with values in a topological space
.

means that ƒ(x) can be made as close as desired to L by making x close enough, but not equal, to p.
The following definitions (known as (ε, δ)-definitions) are the generally accepted ones for the limit of a function in various contexts.
and p,L ∈ R. It is said the limit of f as x approaches p is L and written
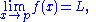
if the following property holds:
Note that the value of the limit does not depend on the value of f(p), nor even that p be in the domain of f.
A more general definition applies for functions defined on subset
s of the real line. Let (a, b) be an open interval in R, and p a point of (a, b). Let f be a real-valued function defined on at least all of (a, b) \ {p}. It is then said that the limit of f as x approaches p is L if, for every real ε > 0, there exists a real δ > 0 such that 0 < | x − p | < δ and x ∈ (a, b) implies | f(x) − L | < ε. Note that the limit does not depend on f(p) being well-defined.
The letters ε and δ can be understood as "error" and "distance", and in fact Cauchy used ε as an abbreviation for "error" in some of his work . In these terms, the error (ε) in the measurement of the value at the limit can be made as small as desired by reducing the distance (δ) to the limit point. As discussed below this definition also works for functions in a more general context. The idea that δ and ε represent distances helps suggest these generalizations.

or
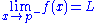
respectively. If both of these limits are equal to L then this can be referred to as the limit of f(x) at p. Conversely, if they are not both equal to L then the limit, as such, does not exist.
A formal definition is as follows. The limit of f(x) as x approaches p from above is L if, for every ε > 0, there exists a δ > 0 such that |f(x) − L| < ε whenever 0 < x − p < δ. The limit of f(x) as x approaches p from below is L if, for every ε > 0, there exists a δ > 0 such that |f(x) − L| < ε whenever 0 < p − x < δ.
If the limit does not exist there is a non-zero oscillation
.
 The function
The function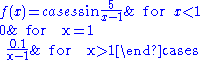
has no limit at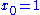 .
.
of M and L ∈ N. It is said that the limit of f as x approaches p is L and write

if the following property holds:
Again, note that p need not be in the domain of f, nor does L need to be in the range of f, and even if f(p) is defined it need not be equal to L.
An alternative definition using the concept of neighbourhood
is as follows:
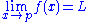
if, for every neighbourhood V of L in B, there exists a neighbourhood U of p in A such that f(U∩M - {p}) ⊆ V.
s with Y a Hausdorff space
. Let p be a limit point
of Ω⊆X, and L ∈Y. For a function f : Ω → Y, it is said that the limit of f as x approaches p is L (i.e., f(x)→L as x→p) and write
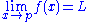
if the following property holds:
This last part of the definition can also be phrased "there exists an open punctured neighbourhood U of p such that f(U∩Ω) ⊆ V ".
Note that the domain of f does not need to contain p. If it does, then the value of f at p is irrelevant to the definition of the limit. In particular, if the domain of f is X - {p} (or all of X), then the limit of f as x → p exists and is equal to L if, for all subsets Ω of X with limit point p, the limit of the restriction of f to Ω exists and is equal to L. Sometimes this criterion is used to establish the non-existence of the two-sided limit of a function on R by showing that the one-sided limit
s either fail to exist or do not agree. Such a view is fundamental in the field of general topology
, where limits and continuity at a point are defined in terms of special families of subsets, called filters
, or generalized sequences known as nets
.
Alternatively, the requirement that Y be a Hausdorff space can be relaxed to the assumption that Y be a general topological space, but then the limit of a function may not be unique. In particular, one can no longer talk about the limit of a function at a point, but rather a limit or the set of limits at a point.
A function is continuous in a limit point p of and in its domain if and only f(p) is the (or, in the general case, a) limit of f(x) as x tends to p.
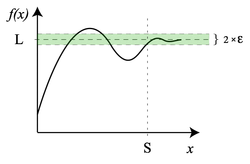 If the extended real line R is considered, i.e., R ∪ {-∞, ∞}, then it is possible to define limits of a function at infinity.
If the extended real line R is considered, i.e., R ∪ {-∞, ∞}, then it is possible to define limits of a function at infinity.
If f(x) is a real function, then the limit of f as x approaches infinity is L, denoted
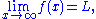
if for all , there exists S > 0 such that
, there exists S > 0 such that
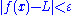 whenever x > S. Or, symbolically:
whenever x > S. Or, symbolically: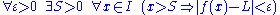
Similarly, the limit of f as x approaches negative infinity is L, denoted
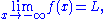
if for all there exists S < 0 such that
there exists S < 0 such that 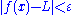 whenever x < S. Or, symbolically:
whenever x < S. Or, symbolically: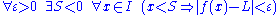
For example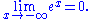
Limits can also have infinite values, for example the limit of f as x approaches a is infinity, denoted
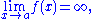
if:
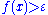 whenever
whenever 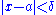 .
.
These ideas can be combined in a natural way to produce definitions for different combinations, such as
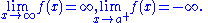
For example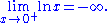
Limits involving infinity are connected with the concept of asymptote
s.
These notions of a limit attempt to provide a metric space interpretation to limits at infinity. However, note that these notions of a limit are consistent with the topological space definition of limit if
In this case, R is a topological space and any function of the form f: X → Y with X, Y⊆ R is subject to the topological definition of a limit. Note that with this topological definition, it is easy to define infinite limits at finite points, which have not been defined above in the metric sense.
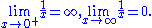
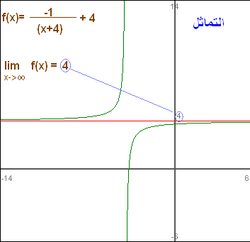 There are three basic rules for evaluating limits at infinity for a rational function
There are three basic rules for evaluating limits at infinity for a rational function
f(x) = p(x)/q(x): (where p and q are polynomials):
If the limit at infinity exists, it represents a horizontal asymptote at y = L. Polynomials do not have horizontal asymptotes; they may occur with rational functions.
with metric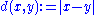 is also a metric space. There are two different types of limits when the complex-valued functions are considered.
is also a metric space. There are two different types of limits when the complex-valued functions are considered.
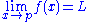
if for all ε > 0 there exists a δ > 0 such that for all real numbers x with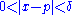 , then
, then 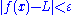 .
.
It is just a particular case of functions over metric spaces with both M and N in the complex plane.
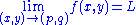
if
where ||(x,y)-(p,q)|| represents the Euclidean distance
.
This can be extended to any number of variables.
If L is the limit (in the sense above) of f as x approaches p, then it is a sequential limit as well, however the converse need not hold in general. If in addition Y is metrizable, then L is the sequential limit of f as x approaches p if and only if it is the limit (in the sense above) of f as x approaches p.
at c if it is both defined at c and its value at c equals the limit of f as x approaches c:
If the condition 0 < |x − c| is left out of the definition of limit, then the resulting definition would be equivalent to requiring f to be continuous at c.
The function f is continuous
at p if and only if the limit of f(x) as x approaches p exists and is equal to f(p). If f : M → N is a function between metric spaces M and N, then it is equivalent that f transforms every sequence in M which converges towards p into a sequence in N which converges towards f(p).
If N is a normed vector space
, then the limit operation is linear in the following sense: if the limit of f(x) as x approaches p is L and the limit of g(x) as x approaches p is P, then the limit of f(x) + g(x) as x approaches p is L + P. If a is a scalar from the base field
, then the limit of af(x) as x approaches p is aL.
If f is a real-valued (or complex-valued) function, then taking the limit is compatible with the algebraic operations, provided the limits on the right sides of the equations below exist (the last identity only holds if the denominator is non-zero). This fact is often called the algebraic limit theorem.
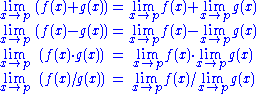
In each case above, when the limits on the right do not exist, or, in the last case, when the limits in both the numerator and the denominator are zero, nonetheless the limit on the left, called an indeterminate form, may still exist—this depends on the functions f and g. These rules are also valid for one-sided limits, for the case p = ±∞, and also for infinite limits using the rules
(see extended real number line
).
Note that there is no general rule for the case q / 0; it all depends on the way 0 is approached. Indeterminate form
s—for instance, 0/0, 0×∞, ∞−∞, and ∞/∞—are also not covered by these rules, but the corresponding limits can often be determined with L'Hôpital's rule
or the Squeeze theorem
.
 , and
, and 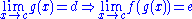 ,
,
is not true. However, this "chain rule" does hold if, in addition, either f(d) = e (i. e. f is continuous at d) or g does not take the value d near c (i. e. there exists a such that if
such that if 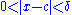 then
then 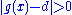 ).
).
The first limit can be proven with the squeeze theorem
. For 0 < x < π/2:
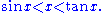
Dividing everything by sin(x) yields
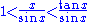

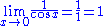
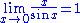
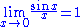
s and has a conditional usage. (It can only be directly used on limits that "equal" 0/0 or ±∞/±∞.
Other indeterminate forms require some algebraic manipulation usually involving setting the limit equal to y, taking the natural logarithm
of both sides, and then applying l'Hôpital's rule
.)
For example:
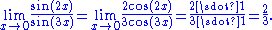
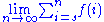
is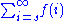 .
.
A short way to write the limit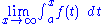
is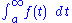 .
.
A short way to write the limit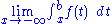
is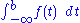 .
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the limit of a function is a fundamental concept in calculus
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
and analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
concerning the behavior of that function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
near a particular input
Independent variable
The terms "dependent variable" and "independent variable" are used in similar but subtly different ways in mathematics and statistics as part of the standard terminology in those subjects...
.
Formal definitions, first devised in the early 19th century, are given below. Informally, a function f assigns an output f(x) to every input x. The function has a limit L at an input p if f(x) is "close" to L whenever x is "close" to p. In other words, f(x) becomes closer and closer to L as x moves closer and closer to p. More specifically, when f is applied to each input sufficiently close to p, the result is an output value that is arbitrarily close to L. If the inputs "close" to p are taken to values that are very different, the limit is said to not exist.
The notion of a limit has many applications in modern calculus. In particular, the many definitions of continuity
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
employ the limit: roughly, a function is continuous if all of its limits agree with the values of the function. It also appears in the definition of the derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
: in the calculus of one variable, this is the limiting value of the slope of secant lines to the graph of a function.
History
Although implicit in the development of calculus of the 17th and 18th centuries, the modern notion of the limit of a function goes back to BolzanoBernard Bolzano
Bernhard Placidus Johann Nepomuk Bolzano , Bernard Bolzano in English, was a Bohemian mathematician, logician, philosopher, theologian, Catholic priest and antimilitarist of German mother tongue.-Family:Bolzano was the son of two pious Catholics...
who, in 1817, introduced the basics of the epsilon-delta technique to define continuous functions. However, his work was not known during his lifetime . Cauchy discussed limits in his Cours d'analyse (1821) and gave essentially the modern definition, but this is not often recognized because he only gave a verbal definition . Weierstrass first introduced the epsilon-delta definition of limit in the form it is usually written today. He also introduced the notations lim and limx→x0 .
The modern notation of placing the arrow below the limit symbol is due to Hardy
G. H. Hardy
Godfrey Harold “G. H.” Hardy FRS was a prominent English mathematician, known for his achievements in number theory and mathematical analysis....
in his book A Course of Pure Mathematics in 1908 .
Motivation
Imagine a person walking over a landscape represented by the graph of y = f(x). His horizontal position is measured by the value of x, much like the position given by a map of the land or by a global positioning system. His altitude is given by the coordinate y. He is walking towards the horizontal position given by x = p. As he gets closer and closer to it, he notices that his altitude approaches L. Say there's a wall there so he can't stand on that point exactly, but can still get arbitrarily close to it. If asked about the altitude of x = p, he would then answer L.What, then, does it mean to say that his altitude approaches L? It means that his altitude gets nearer and nearer to L except for a possible small error in accuracy. For example, suppose a particular accuracy goal is set for our traveler: he must get within ten meters of L in altitude. He reports back that indeed he can get within ten meters of L, since he notes that when he is anywhere within fifty horizontal meters of p, his altitude is always ten meters or less from L.
The accuracy goal is then changed: can he get within one vertical meter? Yes. If he is anywhere within seven horizontal meters of p, then his altitude always remains within one meter from the target L. In summary, to say that the traveler's altitude approaches L as his horizontal position approaches p means that for every target accuracy goal, however small it may be, there is some neighborhood of p whose altitude fulfills that accuracy goal.
The initial informal statement can now be explicated:
- The limit of a function f(x) as x approaches p is a number L with the following property: given any target distance from L, there is a distance from p within which the values of f(x) remain within the target distance.
This explicit statement is quite close to the formal definition of the limit of a function with values in a topological space
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
.
Definitions
To say that
means that ƒ(x) can be made as close as desired to L by making x close enough, but not equal, to p.
The following definitions (known as (ε, δ)-definitions) are the generally accepted ones for the limit of a function in various contexts.
Functions on the real line
Suppose f : R → R is defined on the real lineReal line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
and p,L ∈ R. It is said the limit of f as x approaches p is L and written
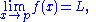
if the following property holds:
- For every real ε > 0, there exists a real δ > 0 such that for all real x, 0 < | x − p | < δ implies | f(x) − L | < ε.
Note that the value of the limit does not depend on the value of f(p), nor even that p be in the domain of f.
A more general definition applies for functions defined on subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
s of the real line. Let (a, b) be an open interval in R, and p a point of (a, b). Let f be a real-valued function defined on at least all of (a, b) \ {p}. It is then said that the limit of f as x approaches p is L if, for every real ε > 0, there exists a real δ > 0 such that 0 < | x − p | < δ and x ∈ (a, b) implies | f(x) − L | < ε. Note that the limit does not depend on f(p) being well-defined.
The letters ε and δ can be understood as "error" and "distance", and in fact Cauchy used ε as an abbreviation for "error" in some of his work . In these terms, the error (ε) in the measurement of the value at the limit can be made as small as desired by reducing the distance (δ) to the limit point. As discussed below this definition also works for functions in a more general context. The idea that δ and ε represent distances helps suggest these generalizations.
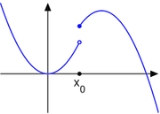
One-sided limits
Alternatively x may approach p from above (right) or below (left), in which case the limits may be written as
or
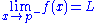
respectively. If both of these limits are equal to L then this can be referred to as the limit of f(x) at p. Conversely, if they are not both equal to L then the limit, as such, does not exist.
A formal definition is as follows. The limit of f(x) as x approaches p from above is L if, for every ε > 0, there exists a δ > 0 such that |f(x) − L| < ε whenever 0 < x − p < δ. The limit of f(x) as x approaches p from below is L if, for every ε > 0, there exists a δ > 0 such that |f(x) − L| < ε whenever 0 < p − x < δ.
If the limit does not exist there is a non-zero oscillation
Oscillation (mathematics)
In mathematics, oscillation is the behaviour of a sequence of real numbers or a real-valued function, which does not converge, but also does not diverge to +∞ or −∞; that is, oscillation is the failure to have a limit, and is also a quantitative measure for that.Oscillation is defined as the...
.
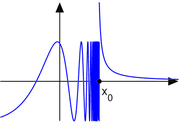
Example of a function without a limit

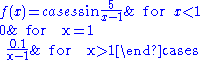
has no limit at
 .
.Functions on metric spaces
Suppose M and N are subsets of metric spaces A and B, respectively, and f : M → N is defined between M and N, with x ∈ M, p a limit pointLimit point
In mathematics, a limit point of a set S in a topological space X is a point x in X that can be "approximated" by points of S in the sense that every neighbourhood of x with respect to the topology on X also contains a point of S other than x itself. Note that x does not have to be an element of S...
of M and L ∈ N. It is said that the limit of f as x approaches p is L and write

if the following property holds:
- For every ε > 0, there exists a δ > 0 such that dB(f(x), L) < ε whenever 0 < dA(x, p) < δ.
Again, note that p need not be in the domain of f, nor does L need to be in the range of f, and even if f(p) is defined it need not be equal to L.
An alternative definition using the concept of neighbourhood
Neighbourhood (mathematics)
In topology and related areas of mathematics, a neighbourhood is one of the basic concepts in a topological space. Intuitively speaking, a neighbourhood of a point is a set containing the point where you can move that point some amount without leaving the set.This concept is closely related to the...
is as follows:
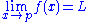
if, for every neighbourhood V of L in B, there exists a neighbourhood U of p in A such that f(U∩M - {p}) ⊆ V.
Functions on topological spaces
Suppose X,Y are topological spaceTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s with Y a Hausdorff space
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
. Let p be a limit point
Limit point
In mathematics, a limit point of a set S in a topological space X is a point x in X that can be "approximated" by points of S in the sense that every neighbourhood of x with respect to the topology on X also contains a point of S other than x itself. Note that x does not have to be an element of S...
of Ω⊆X, and L ∈Y. For a function f : Ω → Y, it is said that the limit of f as x approaches p is L (i.e., f(x)→L as x→p) and write
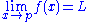
if the following property holds:
- For every open neighborhoodNeighbourhood (mathematics)In topology and related areas of mathematics, a neighbourhood is one of the basic concepts in a topological space. Intuitively speaking, a neighbourhood of a point is a set containing the point where you can move that point some amount without leaving the set.This concept is closely related to the...
V of L, there exists an open neighborhood U of p such that f(U∩Ω- {p}) ⊆ V.
This last part of the definition can also be phrased "there exists an open punctured neighbourhood U of p such that f(U∩Ω) ⊆ V ".
Note that the domain of f does not need to contain p. If it does, then the value of f at p is irrelevant to the definition of the limit. In particular, if the domain of f is X - {p} (or all of X), then the limit of f as x → p exists and is equal to L if, for all subsets Ω of X with limit point p, the limit of the restriction of f to Ω exists and is equal to L. Sometimes this criterion is used to establish the non-existence of the two-sided limit of a function on R by showing that the one-sided limit
One-sided limit
In calculus, a one-sided limit is either of the two limits of a function f of a real variable x as x approaches a specified point either from below or from above...
s either fail to exist or do not agree. Such a view is fundamental in the field of general topology
General topology
In mathematics, general topology or point-set topology is the branch of topology which studies properties of topological spaces and structures defined on them...
, where limits and continuity at a point are defined in terms of special families of subsets, called filters
Filter (mathematics)
In mathematics, a filter is a special subset of a partially ordered set. A frequently used special case is the situation that the ordered set under consideration is just the power set of some set, ordered by set inclusion. Filters appear in order and lattice theory, but can also be found in...
, or generalized sequences known as nets
Net (mathematics)
In mathematics, more specifically in general topology and related branches, a net or Moore–Smith sequence is a generalization of the notion of a sequence. In essence, a sequence is a function with domain the natural numbers, and in the context of topology, the range of this function is...
.
Alternatively, the requirement that Y be a Hausdorff space can be relaxed to the assumption that Y be a general topological space, but then the limit of a function may not be unique. In particular, one can no longer talk about the limit of a function at a point, but rather a limit or the set of limits at a point.
A function is continuous in a limit point p of and in its domain if and only f(p) is the (or, in the general case, a) limit of f(x) as x tends to p.
Limits involving infinity

If f(x) is a real function, then the limit of f as x approaches infinity is L, denoted
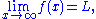
if for all
 , there exists S > 0 such that
, there exists S > 0 such that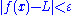 whenever x > S. Or, symbolically:
whenever x > S. Or, symbolically: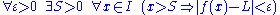
Similarly, the limit of f as x approaches negative infinity is L, denoted
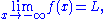
if for all
 there exists S < 0 such that
there exists S < 0 such that 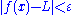 whenever x < S. Or, symbolically:
whenever x < S. Or, symbolically: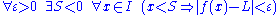
For example
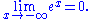
Limits can also have infinite values, for example the limit of f as x approaches a is infinity, denoted
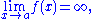
if:
- For all
 there exists
there exists  such that
such that
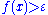 whenever
whenever 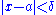 .
.These ideas can be combined in a natural way to produce definitions for different combinations, such as
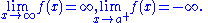
For example
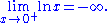
Limits involving infinity are connected with the concept of asymptote
Asymptote
In analytic geometry, an asymptote of a curve is a line such that the distance between the curve and the line approaches zero as they tend to infinity. Some sources include the requirement that the curve may not cross the line infinitely often, but this is unusual for modern authors...
s.
These notions of a limit attempt to provide a metric space interpretation to limits at infinity. However, note that these notions of a limit are consistent with the topological space definition of limit if
- a neighborhood of −∞ is defined to contain an intervalInterval (mathematics)In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
[−∞, c) for some c ∈ R - a neighborhood of ∞ is defined to contain an interval (c, ∞] where c ∈ R
- a neighborhood of a∈R is defined in the normal way metric space R
In this case, R is a topological space and any function of the form f: X → Y with X, Y⊆ R is subject to the topological definition of a limit. Note that with this topological definition, it is easy to define infinite limits at finite points, which have not been defined above in the metric sense.
Alternative notation
Many authors allow for the real projective line to be used as a way to include infinite values as well as extended real line. With this notation, the extended real line is given as R ∪ {-∞, +∞} and the projective real line is R ∪ {∞} where a neighborhood of ∞ is a set of the form {x: |x|>c}. In this notation, for example,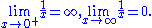
Evaluating limits at infinity for rational functions

Rational function
In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
f(x) = p(x)/q(x): (where p and q are polynomials):
- If the degreeDegree of a polynomialThe degree of a polynomial represents the highest degree of a polynominal's terms , should the polynomial be expressed in canonical form . The degree of an individual term is the sum of the exponents acting on the term's variables...
of p is greater than the degree of q, then the limit is positive or negative infinity depending on the signs of the leading coefficients; - If the degree of p and q are equal, the limit is the leading coefficient of p divided by the leading coefficient of q;
- If the degree of p is less than the degree of q, the limit is 0.
If the limit at infinity exists, it represents a horizontal asymptote at y = L. Polynomials do not have horizontal asymptotes; they may occur with rational functions.
Complex-valued functions
The complex planeComplex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
with metric
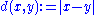 is also a metric space. There are two different types of limits when the complex-valued functions are considered.
is also a metric space. There are two different types of limits when the complex-valued functions are considered.Limit of a function at a point
If f is a complex-valued function, then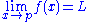
if for all ε > 0 there exists a δ > 0 such that for all real numbers x with
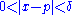 , then
, then 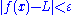 .
.It is just a particular case of functions over metric spaces with both M and N in the complex plane.
Limit of a function of more than one variable
By noting that |x-p| represents a distance, the definition of a limit can be extended to functions of more than one variable. In the case of a function f : R2 → R,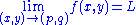
if
- for every ε > 0 there exists a δ > 0 such that for all (x,y) with 0 < ||(x,y)-(p,q)|| < δ, then |f(x,y)-L| < ε
where ||(x,y)-(p,q)|| represents the Euclidean distance
Euclidean distance
In mathematics, the Euclidean distance or Euclidean metric is the "ordinary" distance between two points that one would measure with a ruler, and is given by the Pythagorean formula. By using this formula as distance, Euclidean space becomes a metric space...
.
This can be extended to any number of variables.
Sequential limits
Let f : X → Y be a mapping from a topological space X into a Hausdorff space Y, p∈X and L∈Y.- The sequential limit of f as x→p is L if, for every sequence (xn) in X which convergesLimit of a sequenceThe limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
to p, the sequence f(xn) convergesLimit of a sequenceThe limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
to L.
If L is the limit (in the sense above) of f as x approaches p, then it is a sequential limit as well, however the converse need not hold in general. If in addition Y is metrizable, then L is the sequential limit of f as x approaches p if and only if it is the limit (in the sense above) of f as x approaches p.
Relationship to continuity
The notion of the limit of a function is very closely related to the concept of continuity. A function ƒ is said to be continuousContinuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
at c if it is both defined at c and its value at c equals the limit of f as x approaches c:
If the condition 0 < |x − c| is left out of the definition of limit, then the resulting definition would be equivalent to requiring f to be continuous at c.
Properties
If a function f is real-valued, then the limit of f at p is L if and only if both the right-handed limit and left-handed limit of f at p exist and are equal to L.The function f is continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
at p if and only if the limit of f(x) as x approaches p exists and is equal to f(p). If f : M → N is a function between metric spaces M and N, then it is equivalent that f transforms every sequence in M which converges towards p into a sequence in N which converges towards f(p).
If N is a normed vector space
Normed vector space
In mathematics, with 2- or 3-dimensional vectors with real-valued entries, the idea of the "length" of a vector is intuitive and can easily be extended to any real vector space Rn. The following properties of "vector length" are crucial....
, then the limit operation is linear in the following sense: if the limit of f(x) as x approaches p is L and the limit of g(x) as x approaches p is P, then the limit of f(x) + g(x) as x approaches p is L + P. If a is a scalar from the base field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
, then the limit of af(x) as x approaches p is aL.
If f is a real-valued (or complex-valued) function, then taking the limit is compatible with the algebraic operations, provided the limits on the right sides of the equations below exist (the last identity only holds if the denominator is non-zero). This fact is often called the algebraic limit theorem.
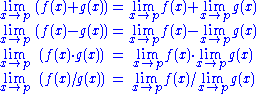
In each case above, when the limits on the right do not exist, or, in the last case, when the limits in both the numerator and the denominator are zero, nonetheless the limit on the left, called an indeterminate form, may still exist—this depends on the functions f and g. These rules are also valid for one-sided limits, for the case p = ±∞, and also for infinite limits using the rules
- q + ∞ = ∞ for q ≠ −∞
- q × ∞ = ∞ if q > 0
- q × ∞ = −∞ if q < 0
- q / ∞ = 0 if q ≠ ± ∞
(see extended real number line
Extended real number line
In mathematics, the affinely extended real number system is obtained from the real number system R by adding two elements: +∞ and −∞ . The projective extended real number system adds a single object, ∞ and makes no distinction between "positive" or "negative" infinity...
).
Note that there is no general rule for the case q / 0; it all depends on the way 0 is approached. Indeterminate form
Indeterminate form
In calculus and other branches of mathematical analysis, an indeterminate form is an algebraic expression obtained in the context of limits. Limits involving algebraic operations are often performed by replacing subexpressions by their limits; if the expression obtained after this substitution...
s—for instance, 0/0, 0×∞, ∞−∞, and ∞/∞—are also not covered by these rules, but the corresponding limits can often be determined with L'Hôpital's rule
L'Hôpital's rule
In calculus, l'Hôpital's rule uses derivatives to help evaluate limits involving indeterminate forms. Application of the rule often converts an indeterminate form to a determinate form, allowing easy evaluation of the limit...
or the Squeeze theorem
Squeeze theorem
In calculus, the squeeze theorem is a theorem regarding the limit of a function....
.
Chain rule
In general, the statement , and
, and 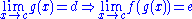 ,
,is not true. However, this "chain rule" does hold if, in addition, either f(d) = e (i. e. f is continuous at d) or g does not take the value d near c (i. e. there exists a
 such that if
such that if 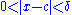 then
then 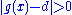 ).
).Limits of special interest
The first limit can be proven with the squeeze theorem
Squeeze theorem
In calculus, the squeeze theorem is a theorem regarding the limit of a function....
. For 0 < x < π/2:
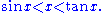
Dividing everything by sin(x) yields
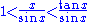

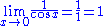
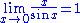
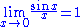
L'Hôpital's rule
This rule uses derivativeDerivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
s and has a conditional usage. (It can only be directly used on limits that "equal" 0/0 or ±∞/±∞.
Other indeterminate forms require some algebraic manipulation usually involving setting the limit equal to y, taking the natural logarithm
Natural logarithm
The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
of both sides, and then applying l'Hôpital's rule
L'Hôpital's rule
In calculus, l'Hôpital's rule uses derivatives to help evaluate limits involving indeterminate forms. Application of the rule often converts an indeterminate form to a determinate form, allowing easy evaluation of the limit...
.)
For example:
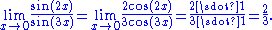
Summations and integrals
A short way to write the limit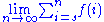
is
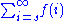 .
.A short way to write the limit
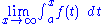
is
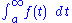 .
.A short way to write the limit
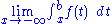
is
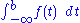 .
.See also
- List of limits
- One-sided limitOne-sided limitIn calculus, a one-sided limit is either of the two limits of a function f of a real variable x as x approaches a specified point either from below or from above...
- Limit of a sequenceLimit of a sequenceThe limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
- Net (topology)
- Big O notationBig O notationIn mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
- Limit superior and limit inferiorLimit superior and limit inferiorIn mathematics, the limit inferior and limit superior of a sequence can be thought of as limiting bounds on the sequence...
- l'Hôpital's ruleL'Hôpital's ruleIn calculus, l'Hôpital's rule uses derivatives to help evaluate limits involving indeterminate forms. Application of the rule often converts an indeterminate form to a determinate form, allowing easy evaluation of the limit...
- Squeeze theoremSqueeze theoremIn calculus, the squeeze theorem is a theorem regarding the limit of a function....