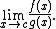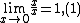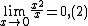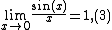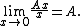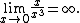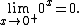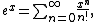Indeterminate form
Encyclopedia
In calculus
and other branches of mathematical analysis
, an indeterminate form is an algebraic expression
obtained in the context of limits
. Limits involving algebraic operations are often performed by replacing subexpressions by their limits; if the expression obtained after this substitution does not give enough information to determine the original limit, it is known as an indeterminate form. The indeterminate forms include 00, 0/0, 1∞, ∞ − ∞, ∞/∞, 0 × ∞, and ∞0.
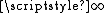, 1, and 0 respectively. In each case, however, if the limits of the numerator and denominator are evaluated and plugged into the division operation, the resulting expression is 0/0. So (roughly speaking) 0/0 can be 0, or 
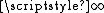, or it can be 1 and, in fact, it is possible to construct similar examples converging to any particular value. That is why the expression 0/0 is indeterminate.
More formally, the fact that the functions
f and g both approach 0 as x approaches some limit point
c is not enough information to evaluate the limit
That limit could converge to any number, or diverge to infinity, or might not exist, depending on what the functions f and g are.
In some theories a value may be defined even where the function is discontinuous. For example |x|/x is undefined for x = 0 in real analysis
. However it is the sign function
with sgn(0) = 0 when considering Fourier series
or hyperfunction
s.
Not every undefined algebraic expression is an indeterminate form. For example, the expression 1/0 is undefined as a real number
but is not indeterminate. This is because any limit that gives rise to this form will diverge to infinity.
An expression representing an indeterminate form may sometimes be given a numerical value in settings other than the computation of limits. The expression 00 is defined as 1 when it represents an empty product
. In the theory of power series
, it is also often treated as 1 by convention, to make certain formula
s more concise. (See the section "Zero to the zero power" in the article on exponentiation
.) In the context of measure theory, it is usual to take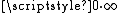
to be 0.
because it often arises in the evaluation of derivative
s using their limit definition.
As mentioned above,
while
This is enough to show that 0/0 is an indeterminate form.
Other examples with this indeterminate form include
and
Direct substitution of the number that x approaches into any of these expressions leads to the indeterminate form 0/0, but the limits take many different values. In fact, any desired value A can be obtained for this indeterminate form as follows:
Furthermore, the value infinity can also be obtained (in the sense of divergence to infinity):
Thus, in general, knowing that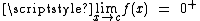
and 
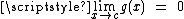is not sufficient to calculate the limit
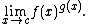
If the functions f and g are analytic
and f is not identically zero in a neighbourhood of c on the complex plane
, then the limit of f(z) g(z) will always be 1. This also holds for real functions, but f must not be negative in the domain of the limit; alternatively, f can be the absolute value of an analytic function.
If the pair (f(x), g(x)) remains between two lines y = mx and y = Mx, where m and M are positive numbers, as x approaches c and f(x) and g(x) approaches 0, then the limit is always 1.
In many settings other than when evaluating limits 00 is taken to be defined as 1 even though it is an indeterminate form; see the section zero to the zero power in the article on exponentiation
. One justification for this is provided by the preceding result. Another is that in power series, such as
when x = 0, then the term in which n = 0 has the correct value only if 00 = 1. Yet another is that in combinatorial
problems one must sometimes take 00 to be an empty product
.
Similarly, any expression of the form a/0, with a≠0 (including a=+∞ and a=-∞), is not an indeterminate since a quotient giving rise to such an expression will always diverge.
Also, 0∞ is sometimes incorrectly thought to be indeterminate, but is not indeterminate: 0+∞=0.
, or other methods can be used to manipulate the expression so that the limit can be evaluated.
For example, the expression x2/x can be simplified to x at any point other than x = 0. Thus, the limit of this expression as x approaches 0 (which depends only on points near 0, not at x = 0 itself) is the limit of x, which is 0. Most of the other examples above can also be evaluated using algebraic simplification.
L'Hôpital's rule is a general method for evaluating the indeterminate forms 0/0 and ∞/∞. This rule states that (under appropriate conditions)
where f' and g' are the derivatives of f and g. (Note that this rule does not apply to forms like ∞/0, 1/0, and so on; but these forms are not indeterminate either.) With luck, these derivatives will allow one to perform algebraic simplification and eventually evaluate the limit.
L'Hôpital's rule can also be applied to other indeterminate forms, using first an appropriate algebraic transformation. For example, to evaluate the form 00:
The right-hand side is of the form ∞/∞, so L'Hôpital's rule applies to it. Notice that this equation is valid (as long as the right-hand side is defined) because the natural logarithm
(ln) is a continuous function
; it's irrelevant how well-behaved f and g may (or may not) be as long as f is asymptotically positive.
Although L'Hôpital's rule applies both to 0/0 and to ∞/∞, one of these may be better than the other in a particular case (because of the possibilities for algebraic simplification afterwards). You can change between these forms, if necessary, by transforming f/g to (1/g)/(1/f).
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
and other branches of mathematical analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, an indeterminate form is an algebraic expression
Algebraic expression
In mathematics, an algebraic expression is an expression that contains only algebraic numbers, variables and algebraic operations. Algebraic operations are addition, subtraction, multiplication, division and exponentiation with integral or fractional exponents...
obtained in the context of limits
Limit of a function
In mathematics, the limit of a function is a fundamental concept in calculus and analysis concerning the behavior of that function near a particular input....
. Limits involving algebraic operations are often performed by replacing subexpressions by their limits; if the expression obtained after this substitution does not give enough information to determine the original limit, it is known as an indeterminate form. The indeterminate forms include 00, 0/0, 1∞, ∞ − ∞, ∞/∞, 0 × ∞, and ∞0.
Discussion
The most common example of an indeterminate form is 0/0. As x approaches 0, the ratios x/x3, x/x, and x2/x go to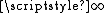, 1, and 0 respectively. In each case, however, if the limits of the numerator and denominator are evaluated and plugged into the division operation, the resulting expression is 0/0. So (roughly speaking) 0/0 can be 0, or 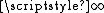, or it can be 1 and, in fact, it is possible to construct similar examples converging to any particular value. That is why the expression 0/0 is indeterminate.More formally, the fact that the functions
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
f and g both approach 0 as x approaches some limit point
Limit point
In mathematics, a limit point of a set S in a topological space X is a point x in X that can be "approximated" by points of S in the sense that every neighbourhood of x with respect to the topology on X also contains a point of S other than x itself. Note that x does not have to be an element of S...
c is not enough information to evaluate the limit
Limit of a function
In mathematics, the limit of a function is a fundamental concept in calculus and analysis concerning the behavior of that function near a particular input....
That limit could converge to any number, or diverge to infinity, or might not exist, depending on what the functions f and g are.
In some theories a value may be defined even where the function is discontinuous. For example |x|/x is undefined for x = 0 in real analysis
Real analysis
Real analysis, is a branch of mathematical analysis dealing with the set of real numbers and functions of a real variable. In particular, it deals with the analytic properties of real functions and sequences, including convergence and limits of sequences of real numbers, the calculus of the real...
. However it is the sign function
Sign function
In mathematics, the sign function is an odd mathematical function that extracts the sign of a real number. To avoid confusion with the sine function, this function is often called the signum function ....
with sgn(0) = 0 when considering Fourier series
Fourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
or hyperfunction
Hyperfunction
In mathematics, hyperfunctions are generalizations of functions, as a 'jump' from one holomorphic function to another at a boundary, and can be thought of informally as distributions of infinite order...
s.
Not every undefined algebraic expression is an indeterminate form. For example, the expression 1/0 is undefined as a real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
but is not indeterminate. This is because any limit that gives rise to this form will diverge to infinity.
An expression representing an indeterminate form may sometimes be given a numerical value in settings other than the computation of limits. The expression 00 is defined as 1 when it represents an empty product
Empty product
In mathematics, an empty product, or nullary product, is the result of multiplying no factors. It is equal to the multiplicative identity 1, given that it exists for the multiplication operation in question, just as the empty sum—the result of adding no numbers—is zero, or the additive...
. In the theory of power series
Series (mathematics)
A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
, it is also often treated as 1 by convention, to make certain formula
Formula
In mathematics, a formula is an entity constructed using the symbols and formation rules of a given logical language....
s more concise. (See the section "Zero to the zero power" in the article on exponentiation
Exponentiation
Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
.) In the context of measure theory, it is usual to take
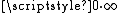to be 0.The form 0/0
The indeterminate form 0/0 is particularly common in calculusCalculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
because it often arises in the evaluation of derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
s using their limit definition.
As mentioned above,
while
This is enough to show that 0/0 is an indeterminate form.
Other examples with this indeterminate form include
and
Direct substitution of the number that x approaches into any of these expressions leads to the indeterminate form 0/0, but the limits take many different values. In fact, any desired value A can be obtained for this indeterminate form as follows:
Furthermore, the value infinity can also be obtained (in the sense of divergence to infinity):
The form 00
The indeterminate form 00 has been discussed since at least 1834. The following examples illustrate that the form is indeterminate:
Thus, in general, knowing that
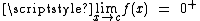and 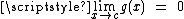is not sufficient to calculate the limit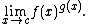If the functions f and g are analytic
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
and f is not identically zero in a neighbourhood of c on the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
, then the limit of f(z) g(z) will always be 1. This also holds for real functions, but f must not be negative in the domain of the limit; alternatively, f can be the absolute value of an analytic function.
If the pair (f(x), g(x)) remains between two lines y = mx and y = Mx, where m and M are positive numbers, as x approaches c and f(x) and g(x) approaches 0, then the limit is always 1.
In many settings other than when evaluating limits 00 is taken to be defined as 1 even though it is an indeterminate form; see the section zero to the zero power in the article on exponentiation
Exponentiation
Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
. One justification for this is provided by the preceding result. Another is that in power series, such as
when x = 0, then the term in which n = 0 has the correct value only if 00 = 1. Yet another is that in combinatorial
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
problems one must sometimes take 00 to be an empty product
Empty product
In mathematics, an empty product, or nullary product, is the result of multiplying no factors. It is equal to the multiplicative identity 1, given that it exists for the multiplication operation in question, just as the empty sum—the result of adding no numbers—is zero, or the additive...
.
Undefined forms that are not indeterminate
The expression 1/0 is not commonly regarded as an indeterminate form because there is not an infinite range of values that f/g could approach. Specifically, if f approaches 1 and g approaches 0, then f and g may be chosen so that: (1) f/g approaches +∞, (2) f/g approaches -∞, or (3) the limit fails to exist. In each case the absolute value |f/g| approaches +∞, and so the quotient f/g must diverge, in the sense of the extended real numbers. (In the framework of the real projective line, the limit is the unsigned infinity ∞ in all three cases.)Similarly, any expression of the form a/0, with a≠0 (including a=+∞ and a=-∞), is not an indeterminate since a quotient giving rise to such an expression will always diverge.
Also, 0∞ is sometimes incorrectly thought to be indeterminate, but is not indeterminate: 0+∞=0.
Evaluating indeterminate forms
The indeterminate nature of a limit's form does not imply that the limit does not exist, as many of the examples above show. In many cases, algebraic elimination, L'Hôpital's ruleL'Hôpital's rule
In calculus, l'Hôpital's rule uses derivatives to help evaluate limits involving indeterminate forms. Application of the rule often converts an indeterminate form to a determinate form, allowing easy evaluation of the limit...
, or other methods can be used to manipulate the expression so that the limit can be evaluated.
For example, the expression x2/x can be simplified to x at any point other than x = 0. Thus, the limit of this expression as x approaches 0 (which depends only on points near 0, not at x = 0 itself) is the limit of x, which is 0. Most of the other examples above can also be evaluated using algebraic simplification.
L'Hôpital's rule is a general method for evaluating the indeterminate forms 0/0 and ∞/∞. This rule states that (under appropriate conditions)
where f
L'Hôpital's rule can also be applied to other indeterminate forms, using first an appropriate algebraic transformation. For example, to evaluate the form 00:
The right-hand side is of the form ∞/∞, so L'Hôpital's rule applies to it. Notice that this equation is valid (as long as the right-hand side is defined) because the natural logarithm
Natural logarithm
The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
(ln) is a continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
; it's irrelevant how well-behaved f and g may (or may not) be as long as f is asymptotically positive.
Although L'Hôpital's rule applies both to 0/0 and to ∞/∞, one of these may be better than the other in a particular case (because of the possibilities for algebraic simplification afterwards). You can change between these forms, if necessary, by transforming f/g to (1/g)/(1/f).
List of indeterminate forms
The following table lists the indeterminate forms for the standard arithmetic operations and the transformations for applying l'Hôpital's rule.| Indeterminate form | Conditions | Transformation to 0/0 | Transformation to ∞/∞ |
|---|---|---|---|
| 0/0 |  |
 |
|
| ∞/∞ |  |
 |
|
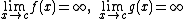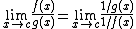| 0 × ∞ |  |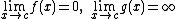
 |
 |
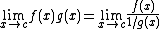| 1∞ |  |
 |
 |
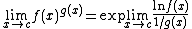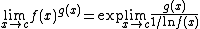| 00 |  |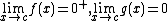
 |
 |
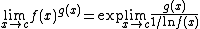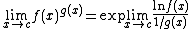| ∞0 |  |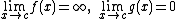
 |
 |
| ∞ − ∞ |  |
 |
 |
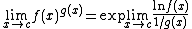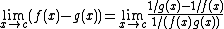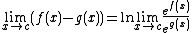See also
- Defined and undefined
- Division by zeroDivision by zeroIn mathematics, division by zero is division where the divisor is zero. Such a division can be formally expressed as a / 0 where a is the dividend . Whether this expression can be assigned a well-defined value depends upon the mathematical setting...
- Extended real number lineExtended real number lineIn mathematics, the affinely extended real number system is obtained from the real number system R by adding two elements: +∞ and −∞ . The projective extended real number system adds a single object, ∞ and makes no distinction between "positive" or "negative" infinity...
- L'Hôpital's ruleL'Hôpital's ruleIn calculus, l'Hôpital's rule uses derivatives to help evaluate limits involving indeterminate forms. Application of the rule often converts an indeterminate form to a determinate form, allowing easy evaluation of the limit...