Right triangle
Encyclopedia
A right triangle or right-angled triangle (British English
) is a triangle
in which one angle
is a right angle
(that is, a 90 degree
angle). The relation between the sides and angles of a right triangle is the basis for trigonometry
.
(side c in the figure above). The sides adjacent to the right angle are called legs (or catheti, singular: cathetus). Side a may be identified as the side adjacent to angle B and opposed to (or opposite) angle A, while side b is the side adjacent to angle A and opposed to angle B.
If the lengths of all three sides of a right triangle are integers, the triangle is said to be a Pythagorean triangle and its side lengths are collectively known as a Pythagorean triple
.
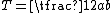
where a and b are the legs of the triangle.
If the incircle
is tangent to the hypotenuse AB at point P, then PA = s – a and PB = s – b, and the area is given by
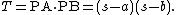
If an altitude
is drawn from the vertex with the right angle to the hypotenuse then the triangle is divided into two smaller triangles which are both similar
to the original and therefore similar to each other. From this:
In equations,
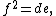(this is sometimes known as the right triangle altitude theorem)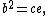
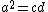
where a, b, c, d, e, f are as shown in the diagram. Thus
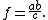
Moreover, the altitude to the hypotenuse is related to the legs of the right triangle by
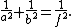
states that:
This can be stated in equation form as c2 = a2 + b2 where c is the length of the hypotenuse and a and b are the lengths of the remaining two sides.
any one of the following statements is true:
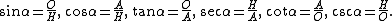
Thales' theorem states that if A is any point of the circle with diameter BC (except B or C themselves) △ABC is a right triangle with A the right angle. The converse states that if a right triangle is inscribed in a circle then the hypotenuse will be a diameter of the circle. A corollary is that the length of the hypotenuse is twice the distance from the right angle vertex to the midpoint of the hypotenuse. Also, the center of the circle that circumscribes
a right triangle is the midpoint of the hypotenuse and its radius is one half the length of the hypotenuse.
s of a right triangle:
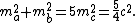
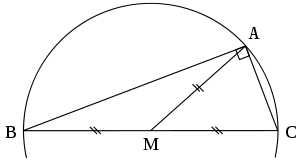
The median on the hypotenuse of a right triangle divides the triangle into two isosceles triangles, because the median equals one-half the hypotenuse.
, the geometric mean
, and the arithmetic mean
of two positive numbers a and b with a > b. If a right triangle has legs H and G and hypotenuse A, then
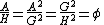
and
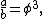
where
is the golden ratio
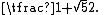
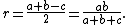
If segments of lengths p and q emanating from vertex C trisect the hypotenuse into segments of length c/3, then
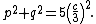
The right triangle is the only triangle having two, rather than three, distinct inscribed squares.
Let h and s (h>s) be the sides of the two inscribed squares in a right triangle with hypotenuse c. Then
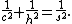
The perimeter of a right triangle equals the sum of the radii of the incircle and the three excircles.
British English
British English, or English , is the broad term used to distinguish the forms of the English language used in the United Kingdom from forms used elsewhere...
) is a triangle
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
in which one angle
Angle
In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
is a right angle
Right angle
In geometry and trigonometry, a right angle is an angle that bisects the angle formed by two halves of a straight line. More precisely, if a ray is placed so that its endpoint is on a line and the adjacent angles are equal, then they are right angles...
(that is, a 90 degree
Degree (angle)
A degree , usually denoted by ° , is a measurement of plane angle, representing 1⁄360 of a full rotation; one degree is equivalent to π/180 radians...
angle). The relation between the sides and angles of a right triangle is the basis for trigonometry
Trigonometry
Trigonometry is a branch of mathematics that studies triangles and the relationships between their sides and the angles between these sides. Trigonometry defines the trigonometric functions, which describe those relationships and have applicability to cyclical phenomena, such as waves...
.
Terminology
The side opposite the right angle is called the hypotenuseHypotenuse
In geometry, a hypotenuse is the longest side of a right-angled triangle, the side opposite the right angle. The length of the hypotenuse of a right triangle can be found using the Pythagorean theorem, which states that the square of the length of the hypotenuse equals the sum of the squares of the...
(side c in the figure above). The sides adjacent to the right angle are called legs (or catheti, singular: cathetus). Side a may be identified as the side adjacent to angle B and opposed to (or opposite) angle A, while side b is the side adjacent to angle A and opposed to angle B.
If the lengths of all three sides of a right triangle are integers, the triangle is said to be a Pythagorean triangle and its side lengths are collectively known as a Pythagorean triple
Pythagorean triple
A Pythagorean triple consists of three positive integers a, b, and c, such that . Such a triple is commonly written , and a well-known example is . If is a Pythagorean triple, then so is for any positive integer k. A primitive Pythagorean triple is one in which a, b and c are pairwise coprime...
.
Area
As with any triangle, the area is equal to one half the base multiplied by the corresponding height. In a right triangle, if one leg is taken as the base then the other is height, so the area of a right triangle is one half the product of the two legs. As a formula the area T is: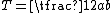where a and b are the legs of the triangle.
If the incircle
Incircle and excircles of a triangle
In geometry, the incircle or inscribed circle of a triangle is the largest circle contained in the triangle; it touches the three sides...
is tangent to the hypotenuse AB at point P, then PA = s – a and PB = s – b, and the area is given by
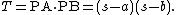
Altitude
If an altitude
Altitude (triangle)
In geometry, an altitude of a triangle is a straight line through a vertex and perpendicular to a line containing the base . This line containing the opposite side is called the extended base of the altitude. The intersection between the extended base and the altitude is called the foot of the...
is drawn from the vertex with the right angle to the hypotenuse then the triangle is divided into two smaller triangles which are both similar
Similarity (geometry)
Two geometrical objects are called similar if they both have the same shape. More precisely, either one is congruent to the result of a uniform scaling of the other...
to the original and therefore similar to each other. From this:
- The altitude is the geometric meanGeometric meanThe geometric mean, in mathematics, is a type of mean or average, which indicates the central tendency or typical value of a set of numbers. It is similar to the arithmetic mean, except that the numbers are multiplied and then the nth root of the resulting product is taken.For instance, the...
(mean proportional) of the two segments of the hypotenuse. - Each leg of the triangle is the mean proportional of the hypotenuse and the adjacent segment.
In equations,
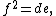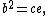
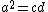
(this is sometimes known as the right triangle altitude theorem)where a, b, c, d, e, f are as shown in the diagram. Thus
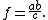
Moreover, the altitude to the hypotenuse is related to the legs of the right triangle by
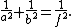
Pythagorean theorem
The Pythagorean theoremPythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
states that:
In any right triangle, the area of the squareSquare (geometry)In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...
whose side is the hypotenuse (the side opposite the right angle) is equal to the sum of the areas of the squares whose sides are the two legs (the two sides that meet at a right angle).
This can be stated in equation form as c2 = a2 + b2 where c is the length of the hypotenuse and a and b are the lengths of the remaining two sides.
Characterizations
A triangle ABC with sides a, b, c (where c is the longest side), circumradius R, and area T is a right triangle if and only ifIf and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
any one of the following statements is true:
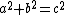
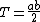
, that is, the longest side is a diameter of the circumcircle.
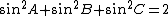
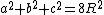
- The circumcircle is tangentTangentIn geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...
to the nine-point circleNine-point circleIn geometry, the nine-point circle is a circle that can be constructed for any given triangle. It is so named because it passes through nine significant points defined from the triangle...
.
Trigonometric ratios
The trigonometric functions for acute angles can be defined as ratios of the sides of a right triangle. For a given angle, a right triangle may be constructed with this angle, and the sides labeled opposite, adjacent and hypotenuse with reference to this angle according to the definitions above. These ratios of the sides do not depend on the particular right triangle chosen, but only on the given angle, since all triangles constructed this way are similar. If, for a given angle α, the opposite side, adjacent side and hypotenuse are labeled O, A and H respectively, then the trigonometric functions are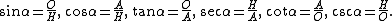Special right triangles
The values of the trigonometric functions can be evaluated exactly for certain angles using right triangles with special angles. These include the 30-60-90 triangle which can be used to evaluate the trigonometric functions for any multiple of π/6, and the 45-45-90 triangle which can be used to evaluate the trigonometric functions for any multiple of π/4.Thales' theorem
Circumscribed circle
In geometry, the circumscribed circle or circumcircle of a polygon is a circle which passes through all the vertices of the polygon. The center of this circle is called the circumcenter....
a right triangle is the midpoint of the hypotenuse and its radius is one half the length of the hypotenuse.
Medians
The following formulas hold for the medianMedian (geometry)
In geometry, a median of a triangle is a line segment joining a vertex to the midpoint of the opposing side. Every triangle has exactly three medians; one running from each vertex to the opposite side...
s of a right triangle:
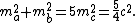
The median on the hypotenuse of a right triangle divides the triangle into two isosceles triangles, because the median equals one-half the hypotenuse.
Relation to various means and the golden ratio
Let H, G, and A be the harmonic meanHarmonic mean
In mathematics, the harmonic mean is one of several kinds of average. Typically, it is appropriate for situations when the average of rates is desired....
, the geometric mean
Geometric mean
The geometric mean, in mathematics, is a type of mean or average, which indicates the central tendency or typical value of a set of numbers. It is similar to the arithmetic mean, except that the numbers are multiplied and then the nth root of the resulting product is taken.For instance, the...
, and the arithmetic mean
Arithmetic mean
In mathematics and statistics, the arithmetic mean, often referred to as simply the mean or average when the context is clear, is a method to derive the central tendency of a sample space...
of two positive numbers a and b with a > b. If a right triangle has legs H and G and hypotenuse A, then
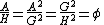
and
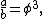
where
is the golden ratioGolden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
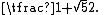
Other properties
The radius of the incircle of a right triangle with legs a and b and hypotenuse c is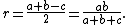If segments of lengths p and q emanating from vertex C trisect the hypotenuse into segments of length c/3, then
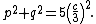
The right triangle is the only triangle having two, rather than three, distinct inscribed squares.
Let h and s (h>s) be the sides of the two inscribed squares in a right triangle with hypotenuse c. Then
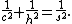
The perimeter of a right triangle equals the sum of the radii of the incircle and the three excircles.