Multivalued function - AbsoluteAstronomy.com

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

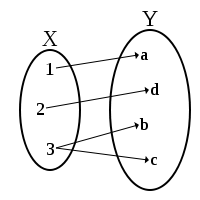
, a multivalued function (shortly: multifunction, other names: set-valued function, set-valued map, multi-valued map, multimap, correspondence, carrier) is a left-total relation; i.e. every input

Input/output

In computing, input/output, or I/O, refers to the communication between an information processing system , and the outside world, possibly a human, or another information processing system. Inputs are the signals or data received by the system, and outputs are the signals or data sent from it...

is associated with one or more output

Output

Output is the term denoting either an exit or changes which exit a system and which activate/modify a process. It is an abstract concept, used in the modeling, system design and system exploitation.-In control theory:...

s. Strictly speaking, a "well-defined" function

Function (mathematics)

In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...

associates one, and only one, output to any particular input. The term "multivalued function" is, therefore, a misnomer

Misnomer

A misnomer is a term which suggests an interpretation that is known to be untrue. Such incorrect terms sometimes derive their names because of the form, action, or origin of the subject becoming named popularly or widely referenced—long before their true natures were known.- Sources of misnomers...

since functions are single-valued. Multivalued functions often arise from functions which are not injective. Such functions do not have an inverse function

Inverse function

In mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...

, but they do have an inverse relation

Inverse relation

In mathematics, the inverse relation of a binary relation is the relation that occurs when you switch the order of the elements in the relation. For example, the inverse of the relation 'child of' is the relation 'parent of'...

. The multivalued function corresponds to this inverse relation.

Examples

Every real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

number greater than zero or every complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...

except 0 has two square root
Square root
In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...

s. The square roots of 4 are in the set {+2,−2}. The square roots of 0 are described by the multiset
Multiset
In mathematics, the notion of multiset is a generalization of the notion of set in which members are allowed to appear more than once...

{0,0}, because 0 is a root of multiplicity
Multiplicity (mathematics)
In mathematics, the multiplicity of a member of a multiset is the number of times it appears in the multiset. For example, the number of times a given polynomial equation has a root at a given point....

2 of the polynomial x².

Each complex number has three cube roots.

The complex logarithm
Complex logarithm
In complex analysis, a complex logarithm function is an "inverse" of the complex exponential function, just as the natural logarithm ln x is the inverse of the real exponential function ex. Thus, a logarithm of z is a complex number w such that ew = z. The notation for such a w is log z...

function is multiple-valued. The values assumed by log(1) are for all integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...

s .

Inverse trigonometric functions are multiple-valued because trigonometric functions are periodic. We have

Consequently arctan(1) is intuitively related to several values: π/4, 5π/4, −3π/4, and so on. We can treat arctan as a single-valued function by restricting the domain of tan x to -π/2 < x < π/2 – a domain over which tan x is monotonically increasing. Thus, the range of arctan(x) becomes -π/2 < y < π/2. These values from a restricted domain are called principal value
Principal value
In considering complex multiple-valued functions in complex analysis, the principal values of a function are the values along one chosen branch of that function, so it is single-valued.-Motivation:...

s.

The indefinite integral is a multivalued function of real-valued functions. The indefinite integral of a function is the set of functions whose derivative is that function. The constant of integration comes follows from the fact that the difference between any two indefinite integrals is a constant,

These are all examples of multivalued functions which come about from non-injective functions. Since the original functions do not preserve all the information of their inputs, they are not reversible. Often, the restriction of a multivalued function is a partial inverse of the original function.

Multivalued functions of a complex variable have branch point

Branch point

In the mathematical field of complex analysis, a branch point of a multi-valued function is a point such that the function is discontinuous when going around an arbitrarily small circuit around this point...

s. For example the nth root and logarithm functions, 0 is a branch point; for the arctangent function, the imaginary units i and −i are branch points. Using the branch points these functions may be redefined to be single valued functions, by restricting the range. A suitable interval may be found through use of a branch cut, a kind of curve which connects pairs of branch points, thus reducing the multilayered Riemann surface of the function to a single layer. As in the case with real functions the restricted range may be called principal branch of the function.

Riemann surfaces

A more sophisticated viewpoint replaces "multivalued functions" with functions whose domain is a Riemann surface

Riemann surface

In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...

(so named in honor of Bernhard Riemann

Bernhard Riemann

Georg Friedrich Bernhard Riemann was an influential German mathematician who made lasting contributions to analysis and differential geometry, some of them enabling the later development of general relativity....

Set-valued analysis

Set-valued analysis is the generalization, to set-valued functions, of ideas from mathematical analysis

Mathematical analysis

Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...

and topology

Topology

Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...

such as continuity, differentiation, integration

Integral

Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...

, implicit function theorem

Implicit function theorem

In multivariable calculus, the implicit function theorem is a tool which allows relations to be converted to functions. It does this by representing the relation as the graph of a function. There may not be a single function whose graph is the entire relation, but there may be such a function on...

, contraction mapping

Contraction mapping

In mathematics, a contraction mapping, or contraction, on a metric space is a function f from M to itself, with the property that there is some nonnegative real number k...

s, measure theory, fixed-point theorem

Fixed-point theorem

In mathematics, a fixed-point theorem is a result saying that a function F will have at least one fixed point , under some conditions on F that can be stated in general terms...

s, optimization

Optimization (mathematics)

In mathematics, computational science, or management science, mathematical optimization refers to the selection of a best element from some set of available alternatives....

, topological degree theory

Topological degree theory

In mathematics, topological degree theory is a generalization of the winding number of a curve in the complex plane. It can be used to estimate the number of solutions of an equation, and is closely connected to fixed-point theory. When one solution of an equation is easily found, degree theory can...

. Equation

Equation

An equation is a mathematical statement that asserts the equality of two expressions. In modern notation, this is written by placing the expressions on either side of an equals sign , for examplex + 3 = 5\,asserts that x+3 is equal to 5...

s and inequalities can be generalized to intervals

Interval (mathematics)

In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...

and then to inclusions.

Types of multivalued functions

One can differentiate many continuity concepts, primarily closed graph property and upper and lower hemicontinuity

Hemicontinuity

In mathematics, the notion of the continuity of functions is not immediately extendible to multi-valued mappings or correspondences. The dual concepts of upper hemicontinuity and lower hemicontinuity facilitate such an extention...

. (One should be warned that often the terms upper and lower semicontinuous are used instead of upper and lower hemicontinuous reserved for the case of weak topology in domain; yet we arrive at the collision with the reserved names for upper and lower semicontinuous real-valued function). There exist also various definitions for measurability of multifunction.

History

The practice of allowing function in mathematics to mean also multivalued function dropped out of usage at some point in the first half of the twentieth century. Some evolution can be seen in different editions of A Course of Pure Mathematics
A Course of Pure Mathematics
A Course of Pure Mathematics is a classic textbook in introductory mathematical analysis, written by G. H. Hardy. It is recommended for people studying calculus. First published in 1908, it went through ten editions and several reprints. It is now out of copyright in UK and is downloadable from...

by G. H. Hardy

G. H. Hardy

Godfrey Harold “G. H.” Hardy FRS was a prominent English mathematician, known for his achievements in number theory and mathematical analysis....

, for example. It probably persisted longest in the theory of special functions, for its occasional convenience.

The theory of multivalued functions was fairly systematically developed for the first time
in C. Berge "Topological spaces" 1963.

Applications

Multifunctions arise in optimal control theory

Optimal control

Optimal control theory, an extension of the calculus of variations, is a mathematical optimization method for deriving control policies. The method is largely due to the work of Lev Pontryagin and his collaborators in the Soviet Union and Richard Bellman in the United States.-General method:Optimal...

, especially differential inclusions and related subjects as game theory

Game theory

Game theory is a mathematical method for analyzing calculated circumstances, such as in games, where a person’s success is based upon the choices of others...

, where the Kakutani fixed point theorem

Kakutani fixed point theorem

In mathematical analysis, the Kakutani fixed-point theorem is a fixed-point theorem for set-valued functions. It provides sufficient conditions for a set-valued function defined on a convex, compact subset of a Euclidean space to have a fixed point, i.e. a point which is mapped to a set containing...

for multifunctions has been applied to prove existence of Nash equilibria

Nash equilibrium

In game theory, Nash equilibrium is a solution concept of a game involving two or more players, in which each player is assumed to know the equilibrium strategies of the other players, and no player has anything to gain by changing only his own strategy unilaterally...

. This amongst many other properties loosely associated with approximability of upper hemicontinuous multifunctions via continuous functions explains why upper hemicontinuity is more preferred than lower hemicontinuity.

Nevertheless, lower hemicontinuous multifunctions usually possess continuous selections as stated in the Michael selection theorem

Michael selection theorem

In functional analysis, a branch of mathematics, the most popular version of the Michael selection theorem, named after Ernest Michael, states the following:- Other selection theorems :* Zero-dimensional Michael selection theorem...

which provides another characterisation of paracompact spaces (see: E. Michael, Continuous selections I" Ann. of Math. (2) 63 (1956), and D. Repovs, P.V. Semenov, Ernest Michael and theory of continuous selections" arXiv:0803.4473v1). Other selection theorems, like Bressan-Colombo directional continuous selection, Kuratowski—Ryll-Nardzewski measurable selection, Aumann measurable selection, Fryszkowski selection for decomposable maps are important in optimal control

Optimal control

and the theory of differential inclusions.

In physics, multivalued functions play an increasingly
important role. They form the mathematical basis for Dirac

Paul Dirac

Paul Adrien Maurice Dirac, OM, FRS was an English theoretical physicist who made fundamental contributions to the early development of both quantum mechanics and quantum electrodynamics...

's magnetic monopole

Magnetic monopole

A magnetic monopole is a hypothetical particle in particle physics that is a magnet with only one magnetic pole . In more technical terms, a magnetic monopole would have a net "magnetic charge". Modern interest in the concept stems from particle theories, notably the grand unified and superstring...

s, for the theory
of defect

Crystallographic defect

Crystalline solids exhibit a periodic crystal structure. The positions of atoms or molecules occur on repeating fixed distances, determined by the unit cell parameters. However, the arrangement of atom or molecules in most crystalline materials is not perfect...

s in crystal and the resulting plasticity

Plasticity (physics)

In physics and materials science, plasticity describes the deformation of a material undergoing non-reversible changes of shape in response to applied forces. For example, a solid piece of metal being bent or pounded into a new shape displays plasticity as permanent changes occur within the...

of materials,
for vortices

Vortex

A vortex is a spinning, often turbulent,flow of fluid. Any spiral motion with closed streamlines is vortex flow. The motion of the fluid swirling rapidly around a center is called a vortex...

in superfluid

Superfluid

Superfluidity is a state of matter in which the matter behaves like a fluid without viscosity and with extremely high thermal conductivity. The substance, which appears to be a normal liquid, will flow without friction past any surface, which allows it to continue to circulate over obstructions and...

s and superconductors, and for phase transition

Phase transition

A phase transition is the transformation of a thermodynamic system from one phase or state of matter to another.A phase of a thermodynamic system and the states of matter have uniform physical properties....

s in these systems, for instance melting

Melting

Melting, or fusion, is a physical process that results in the phase change of a substance from a solid to a liquid. The internal energy of a substance is increased, typically by the application of heat or pressure, resulting in a rise of its temperature to the melting point, at which the rigid...

and quark confinement.
They are the origin of gauge field structures in many branches of physics.