Principal branch
Encyclopedia
In mathematics
, a principal branch is a function which selects one branch, or "slice", of a multi-valued function. Most often, this applies to functions defined on the complex plane
: see branch cut.
One way to view a principal branch is to look specifically at the exponential function
, and the logarithm
, as it is defined in complex analysis
.
The exponential function is single-valued, where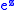
is defined as:
where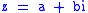
.
However, the periodic nature of the trigonometric functions involved makes it clear that the logarithm is not so uniquely determined. One way to see this is to look at the following:
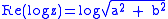
and
where k is any integer.
Any number log(z) defined by such criteria has the property that elog(z) = z.
In this manner log function is a multi-valued function (often referred to as a "multifunction" in the context of complex analysis). A branch cut, usually along the negative real axis, can limit the imaginary part so it lies between −π and π. These are the chosen principal value
s.
This is the principal branch of the log function. Often it is defined using a capital letter, Log(z).
A more familiar principal branch function, limited to real numbers, is that of a positive real number raised to the power of 1/2.
For example, take the relation y = x1/2, where x is any positive real number.
This relation can be satisfied by any value of y equal to a square root
of x (either positive or negative). When y is taken to be the positive square root, we write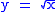
.
In this instance, the positive square root function is taken as the principal branch of the multi-valued relation x1/2.
Principal branches are also used in the definition of many inverse trigonometric
functions.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a principal branch is a function which selects one branch, or "slice", of a multi-valued function. Most often, this applies to functions defined on the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
: see branch cut.
One way to view a principal branch is to look specifically at the exponential function
Exponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
, and the logarithm
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
, as it is defined in complex analysis
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
.
The exponential function is single-valued, where
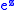is defined as:where
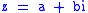.However, the periodic nature of the trigonometric functions involved makes it clear that the logarithm is not so uniquely determined. One way to see this is to look at the following:
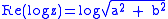
and
where k is any integer.
Any number log(z) defined by such criteria has the property that elog(z) = z.
In this manner log function is a multi-valued function (often referred to as a "multifunction" in the context of complex analysis). A branch cut, usually along the negative real axis, can limit the imaginary part so it lies between −π and π. These are the chosen principal value
Principal value
In considering complex multiple-valued functions in complex analysis, the principal values of a function are the values along one chosen branch of that function, so it is single-valued.-Motivation:...
s.
This is the principal branch of the log function. Often it is defined using a capital letter, Log(z).
A more familiar principal branch function, limited to real numbers, is that of a positive real number raised to the power of 1/2.
For example, take the relation y = x1/2, where x is any positive real number.
This relation can be satisfied by any value of y equal to a square root
Square root
In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
of x (either positive or negative). When y is taken to be the positive square root, we write
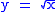.In this instance, the positive square root function is taken as the principal branch of the multi-valued relation x1/2.
Principal branches are also used in the definition of many inverse trigonometric
Trigonometry
Trigonometry is a branch of mathematics that studies triangles and the relationships between their sides and the angles between these sides. Trigonometry defines the trigonometric functions, which describe those relationships and have applicability to cyclical phenomena, such as waves...
functions.