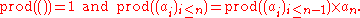Empty product
Encyclopedia
In mathematics
, an empty product, or nullary product, is the result of multiplying
no factors. It is equal to the multiplicative identity
1, given that it exists for the multiplication operation in question, just as the empty sum
—the result of adding
no numbers—is zero
, or the additive identity.
When a mathematical recipe says "multiply all the numbers in this list", and the list contains, say, 2, 3, 2 and 4, we multiply first the first number by the second, then the result by the third, and so on until the end of the list, so the product of (2,3,2,4) would be 48. If the list contains only one number, so that we cannot multiply first by second, common convention holds that the 'product of all' is that same number, and if the list has no numbers at all, the 'product of all' is 1. This value is necessary to be consistent with the recursive
definition of what a product over a sequence (or set, given commutativity) means. For example,
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an empty product, or nullary product, is the result of multiplying
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
no factors. It is equal to the multiplicative identity
Identity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
1, given that it exists for the multiplication operation in question, just as the empty sum
Empty sum
In mathematics, an empty sum, or nullary sum, is a summation involving no terms at all. The value of any empty sum of numbers is conventionally taken to be zero...
—the result of adding
Addition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
no numbers—is zero
0 (number)
0 is both a numberand the numerical digit used to represent that number in numerals.It fulfills a central role in mathematics as the additive identity of the integers, real numbers, and many other algebraic structures. As a digit, 0 is used as a placeholder in place value systems...
, or the additive identity.
When a mathematical recipe says "multiply all the numbers in this list", and the list contains, say, 2, 3, 2 and 4, we multiply first the first number by the second, then the result by the third, and so on until the end of the list, so the product of (2,3,2,4) would be 48. If the list contains only one number, so that we cannot multiply first by second, common convention holds that the 'product of all' is that same number, and if the list has no numbers at all, the 'product of all' is 1. This value is necessary to be consistent with the recursive
Recursion
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
definition of what a product over a sequence (or set, given commutativity) means. For example,
-

In general, we define
The empty product is used in discrete mathematicsDiscrete mathematicsDiscrete mathematics is the study of mathematical structures that are fundamentally discrete rather than continuous. In contrast to real numbers that have the property of varying "smoothly", the objects studied in discrete mathematics – such as integers, graphs, and statements in logic – do not...
, algebraElementary algebraElementary algebra is a fundamental and relatively basic form of algebra taught to students who are presumed to have little or no formal knowledge of mathematics beyond arithmetic. It is typically taught in secondary school under the term algebra. The major difference between algebra and...
, the study of power series, and computer programs.
The term "empty product" is most often used in the above sense when discussing arithmeticArithmeticArithmetic or arithmetics is the oldest and most elementary branch of mathematics, used by almost everyone, for tasks ranging from simple day-to-day counting to advanced science and business calculations. It involves the study of quantity, especially as the result of combining numbers...
operations. However, the term is sometimes employed when discussing set-theoretic intersections, categorical products, and products in computer programming; these are discussed below.
Intuitive justification
Imagine a calculatorCalculatorAn electronic calculator is a small, portable, usually inexpensive electronic device used to perform the basic operations of arithmetic. Modern calculators are more portable than most computers, though most PDAs are comparable in size to handheld calculators.The first solid-state electronic...
that can only multiply.
It has an "ENTER" key and a "CLEAR" key.
One would wish that, for example, if one presses "CLEAR", 7 "ENTER", 3 "ENTER", 4 "ENTER", then the display reads 84, because 7 × 3 × 4 = 84. More precisely, we specify:
- A number is displayed just after "CLEAR" is pressed;
- When a number is displayed and one enters another number, the product is displayed;
- When "CLEAR" is pressed and then some numbers are entered, their product is displayed.
Then the starting value after pressing "CLEAR" has to be 1. After one has pressed "clear" and done nothing else, the number of factors one has entered is zero. Therefore the product of zero numbers is 1.
Frequent examples
Two often-seen instances are a0 = 1 (any number raised to the zeroth powerExponentiationExponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
is one) and 0! = 1 (the factorialFactorialIn mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
of zero is one).
More examples of the use of the empty product in mathematics may be found in the binomial theoremBinomial theoremIn elementary algebra, the binomial theorem describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the power n into a sum involving terms of the form axbyc, where the exponents b and c are nonnegative integers with , and the coefficient a of...
, factorialFactorialIn mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
, fundamental theorem of arithmeticFundamental theorem of arithmeticIn number theory, the fundamental theorem of arithmetic states that any integer greater than 1 can be written as a unique product of prime numbers...
, birthday paradoxBirthday paradoxIn probability theory, the birthday problem or birthday paradox pertains to the probability that, in a set of n randomly chosen people, some pair of them will have the same birthday. By the pigeonhole principle, the probability reaches 100% when the number of people reaches 366. However, 99%...
, Stirling numberStirling numberIn mathematics, Stirling numbers arise in a variety of combinatorics problems. They are named after James Stirling, who introduced them in the 18th century. Two different sets of numbers bear this name: the Stirling numbers of the first kind and the Stirling numbers of the second...
, König's theoremKönig's theorem (set theory)In set theory, König's theorem colloquially states that if the axiom of choice holds, I is a set, mi and ni are cardinal numbers for every i in I, and m_i In set theory, König's theorem In set theory, König's theorem (named after the Hungarian mathematician Gyula Kőnig, who published under the...
, binomial type, difference operator, Pochhammer symbolPochhammer symbolIn mathematics, the Pochhammer symbol introduced by Leo August Pochhammer is the notation ', where is a non-negative integer. Depending on the context the Pochhammer symbol may represent either the rising factorial or the falling factorial as defined below. Care needs to be taken to check which...
, proof that e is irrationalProof that e is irrationalIn mathematics, the series representation of Euler's number ecan be used to prove that e is irrational. Of the many representations of e, this is the Taylor series for the exponential function evaluated at y = 1.-Summary of the proof:...
, prime factorPrime factorIn number theory, the prime factors of a positive integer are the prime numbers that divide that integer exactly, without leaving a remainder. The process of finding these numbers is called integer factorization, or prime factorization. A prime factor can be visualized by understanding Euclid's...
, binomial seriesBinomial seriesIn mathematics, the binomial series is the Taylor series at x = 0 of the function f given by f = α, where is an arbitrary complex number...
, and multisetMultisetIn mathematics, the notion of multiset is a generalization of the notion of set in which members are allowed to appear more than once...
.
Logarithms
The definition of an empty product can be based on that of the empty sumEmpty sumIn mathematics, an empty sum, or nullary sum, is a summation involving no terms at all. The value of any empty sum of numbers is conventionally taken to be zero...
:
The sum of two logarithmLogarithmThe logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
s is equal to the logarithm of the product of their operands, i.e. for any base b > 0:

and
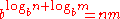
and more generally

i.e., multiplication across all elements of a set is b to the power of the sum of all logarithms of the set's elements.
Using this property as definition, and extending this to the empty product, the right-hand side of this equation evaluates to b0 for the empty setEmpty setIn mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
, because the empty sum is defined to be zero, and therefore the empty product must equal one.
0 raised to the 0th power
In set theory and combinatorics, the cardinal numberCardinal numberIn mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
nm is the size of the set of functions from a set of size m into a set of size n. If m is positive and n is zero, then there are no such functions, because there are no elements in the latter set to map those of the former set into. Thus 0m = 0 when m is positive. However, if both sets are empty (have size 0), then there is exactly one such function — the empty functionEmpty functionIn mathematics, an empty function is a function whose domain is the empty set. For each set A, there is exactly one such empty functionf_A: \varnothing \rightarrow A....
. For this reason, authors in combinatorics and set theory frequently define 00 to be 1 when it represents an empty product.
Nullary conjunction and intersection
For similar reasons, the logical conjunctionLogical conjunctionIn logic and mathematics, a two-place logical operator and, also known as logical conjunction, results in true if both of its operands are true, otherwise the value of false....
of no argument is the tautologyTautology (logic)In logic, a tautology is a formula which is true in every possible interpretation. Philosopher Ludwig Wittgenstein first applied the term to redundancies of propositional logic in 1921; it had been used earlier to refer to rhetorical tautologies, and continues to be used in that alternate sense...
. Accordingly the intersectionIntersection (set theory)In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
of no set is conventionally equal to the universe. See nullary intersection for more information.
Nullary Cartesian product
Consider the general definition of the Cartesian productCartesian productIn mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
:
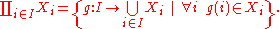
If I is empty, the only satisfying g is the empty functionEmpty functionIn mathematics, an empty function is a function whose domain is the empty set. For each set A, there is exactly one such empty functionf_A: \varnothing \rightarrow A....
 :
:
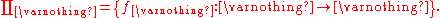
Thus, the cardinality of the Cartesian product of no sets is 1.
Under the perhaps more familiar n-tupleTupleIn mathematics and computer science, a tuple is an ordered list of elements. In set theory, an n-tuple is a sequence of n elements, where n is a positive integer. There is also one 0-tuple, an empty sequence. An n-tuple is defined inductively using the construction of an ordered pair...
interpretation,

that is, the singleton set containing the empty tuple. Note that in both representations the empty product has cardinality 1.
Nullary Cartesian product of functions
The empty Cartesian product of functions is again the empty function.
Nullary categorical product
In any category, the productProduct (category theory)In category theory, the product of two objects in a category is a notion designed to capture the essence behind constructions in other areas of mathematics such as the cartesian product of sets, the direct product of groups, the direct product of rings and the product of topological spaces...
of an empty family is a terminal object of that category. This can be demonstrated by using the limitLimit (category theory)In category theory, a branch of mathematics, the abstract notion of a limit captures the essential properties of universal constructions such as products and inverse limits....
definition of the product. An n-fold categorical product can be defined as the limit with respect to a diagramDiagram (category theory)In category theory, a branch of mathematics, a diagram is the categorical analogue of an indexed family in set theory. The primary difference is that in the categorical setting one has morphisms. An indexed family of sets is a collection of sets, indexed by a fixed set; equivalently, a function...
given by the discrete categoryDiscrete categoryIn mathematics, especially category theory, a discrete category is a category whose only morphisms are the identity morphisms. It is the simplest kind of category...
with n objects. An empty product is then given by the limit with respect to the empty category, which is the terminal object of the category if it exists. This definition specializes to give results as above. For example, in the category of setsCategory of setsIn the mathematical field of category theory, the category of sets, denoted as Set, is the category whose objects are sets. The arrows or morphisms between sets A and B are all functions from A to B...
the categorical product is the usual Cartesian product, and the terminal object is a singleton set. In the category of groupsCategory of groupsIn mathematics, the category Grp has the class of all groups for objects and group homomorphisms for morphisms. As such, it is a concrete category...
the categorical product is the Cartesian product of groups, and the terminal object is a trivial group with one element. To obtain the usual arithmetic definition of the empty product we must take the decategorification of the empty product in the category of finite sets.
DuallyDual (category theory)In category theory, a branch of mathematics, duality is a correspondence between properties of a category C and so-called dual properties of the opposite category Cop...
, the coproductCoproductIn category theory, the coproduct, or categorical sum, is the category-theoretic construction which includes the disjoint union of sets and of topological spaces, the free product of groups, and the direct sum of modules and vector spaces. The coproduct of a family of objects is essentially the...
of an empty family is an initial objectInitial objectIn category theory, an abstract branch of mathematics, an initial object of a category C is an object I in C such that for every object X in C, there exists precisely one morphism I → X...
.
Nullary categorical products or coproducts may not exist in a given category; e.g. in the category of fields, neither exists.
In computer programming
Many programming languages, such as PythonPython (programming language)Python is a general-purpose, high-level programming language whose design philosophy emphasizes code readability. Python claims to "[combine] remarkable power with very clear syntax", and its standard library is large and comprehensive...
, allow the direct expression of lists of numbers, and even functions that allow an arbitrary number of parameters. If such a language has a function that returns the product of all the numbers in a list, it usually works like this:
listprod( [2,3,5] ) --> 30
listprod( [2,3] ) --> 6
listprod( [2] ) --> 2
listprod( [] ) --> 1
This convention sometimes helps avoid having to code special cases like "if length of list is 1" or "if length of list is zero" as special cases.
Many programming languages do not permit the direct expression of the empty product, because they do not allow expressing lists. Multiplication is taken to be an infixInfix notationInfix notation is the common arithmetic and logical formula notation, in which operators are written infix-style between the operands they act on . It is not as simple to parse by computers as prefix notation or postfix notation Infix notation is the common arithmetic and logical formula notation,...
operator and therefore a binary operator. (A programmer may, of course, implement it.) Languages implementing variadic functionVariadic functionIn computer programming, a variadic function is a function of indefinite arity, i.e., one which accepts a variable number of arguments. Support for variadic functions differs widely among programming languages....
s are the exception. For example, the fully parenthesized prefix notationS-expressionS-expressions or sexps are list-based data structures that represent semi-structured data. An S-expression may be a nested list of smaller S-expressions. S-expressions are probably best known for their use in the Lisp family of programming languages...
of Lisp languagesLisp programming languageLisp is a family of computer programming languages with a long history and a distinctive, fully parenthesized syntax. Originally specified in 1958, Lisp is the second-oldest high-level programming language in widespread use today; only Fortran is older...
gives rise to a natural notation for nullary functions:
(* 2 2 2) ; evaluates to 8
(* 2 2) ; evaluates to 4
(* 2) ; evaluates to 2
(*) ; evaluates to 1
External links
-