
Cartesian closed category
Encyclopedia
In category theory
, a category is cartesian closed if, roughly speaking, any morphism
defined on a product
of two objects can be naturally identified with a morphism defined on one of the factors. These categories are particularly important in mathematical logic
and the theory of programming, in that they provide a natural setting for lambda calculus
. For generalizations of this notion to monoidal categories
, see closed monoidal category
.
it satisfies the following three properties:
The first two conditions can be combined to the single requirement that any finite (possibly empty) family of objects of C admit a product
in C, because of the natural associativity
of the categorical product and because the empty product
in a category is the terminal object of that category.
The third condition is equivalent to the requirement that the functor
–×Y (i.e. the functor from C to C that maps objects X to X×Y and morphisms φ to φ×idY) has a right adjoint
, usually denoted –Y, for all objects Y in C.
For locally small categories, this can be expressed by the existence of a bijection
between the hom-sets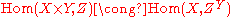
which is natural
in both X and Z.
If a category is such that all its slice categories are cartesian closed, then it is called locally cartesian closed.
The following categories are not cartesian closed:
applications, this is known as currying
; it has led to the realization that simply-typed lambda calculus can be interpreted in any cartesian closed category.
The Curry-Howard-Lambek correspondence provides a deep isomorphism between intuitionistic logic, simply-typed lambda calculus and cartesian closed categories.
Certain cartesian closed categories, the topoi
, have been proposed as a general setting for mathematics, instead of traditional set theory
.
The renowned computer scientist John Backus
has advocated a variable-free notation, or Function-level programming
, which in retrospect bears some similarity to the internal language of cartesian closed categories. CAML is more consciously modelled on cartesian closed categories.
z = (xz)y.
One may ask what other such equations are valid in all cartesian closed categories. It turns out that all of them follow logically from the following axioms:
Bicartesian closed categories extend cartesian closed categories with binary coproduct
s and an initial object
, with products distributing over coproducts. Their equational theory is extended with the following axioms:
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, a category is cartesian closed if, roughly speaking, any morphism
Morphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
defined on a product
Product (category theory)
In category theory, the product of two objects in a category is a notion designed to capture the essence behind constructions in other areas of mathematics such as the cartesian product of sets, the direct product of groups, the direct product of rings and the product of topological spaces...
of two objects can be naturally identified with a morphism defined on one of the factors. These categories are particularly important in mathematical logic
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
and the theory of programming, in that they provide a natural setting for lambda calculus
Lambda calculus
In mathematical logic and computer science, lambda calculus, also written as λ-calculus, is a formal system for function definition, function application and recursion. The portion of lambda calculus relevant to computation is now called the untyped lambda calculus...
. For generalizations of this notion to monoidal categories
Monoidal category
In mathematics, a monoidal category is a category C equipped with a bifunctorwhich is associative, up to a natural isomorphism, and an object I which is both a left and right identity for ⊗, again up to a natural isomorphism...
, see closed monoidal category
Closed monoidal category
In mathematics, especially in category theory, aclosed monoidal category is a context where we can take tensor products of objects and also form 'mapping objects'. A classic example is the category of sets, Set, where the tensor product of sets A and B is the usual cartesian product A \times B, and...
.
Definition
The category C is called Cartesian closed if and only ifIf and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
it satisfies the following three properties:
- It has a terminal object.
- Any two objects X and Y of C have a productProduct (category theory)In category theory, the product of two objects in a category is a notion designed to capture the essence behind constructions in other areas of mathematics such as the cartesian product of sets, the direct product of groups, the direct product of rings and the product of topological spaces...
X×Y in C. - Any two objects Y and Z of C have an exponentialExponential objectIn mathematics, specifically in category theory, an exponential object is the categorical equivalent of a function space in set theory. Categories with all finite products and exponential objects are called cartesian closed categories...
ZY in C.
The first two conditions can be combined to the single requirement that any finite (possibly empty) family of objects of C admit a product
Product (category theory)
In category theory, the product of two objects in a category is a notion designed to capture the essence behind constructions in other areas of mathematics such as the cartesian product of sets, the direct product of groups, the direct product of rings and the product of topological spaces...
in C, because of the natural associativity
Associativity
In mathematics, associativity is a property of some binary operations. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not...
of the categorical product and because the empty product
Empty product
In mathematics, an empty product, or nullary product, is the result of multiplying no factors. It is equal to the multiplicative identity 1, given that it exists for the multiplication operation in question, just as the empty sum—the result of adding no numbers—is zero, or the additive...
in a category is the terminal object of that category.
The third condition is equivalent to the requirement that the functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
–×Y (i.e. the functor from C to C that maps objects X to X×Y and morphisms φ to φ×idY) has a right adjoint
Adjoint functors
In mathematics, adjoint functors are pairs of functors which stand in a particular relationship with one another, called an adjunction. The relationship of adjunction is ubiquitous in mathematics, as it rigorously reflects the intuitive notions of optimization and efficiency...
, usually denoted –Y, for all objects Y in C.
For locally small categories, this can be expressed by the existence of a bijection
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
between the hom-sets
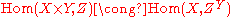
which is natural
Natural transformation
In category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Indeed this intuition...
in both X and Z.
If a category is such that all its slice categories are cartesian closed, then it is called locally cartesian closed.
Examples
Examples of cartesian closed categories include:- The category Set of all sets, with functionFunction (mathematics)In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s as morphisms, is cartesian closed. The product X×Y is the cartesian product of X and Y, and ZY is the set of all functions from Y to Z. The adjointness is expressed by the following fact: the function f : X×Y → Z is naturally identified with the curriedCurryingIn mathematics and computer science, currying is the technique of transforming a function that takes multiple arguments in such a way that it can be called as a chain of functions each with a single argument...
function g : X → ZY defined by g(x)(y) = f(x,y) for all x in X and y in Y. - The category of finite sets, with functions as morphisms, is cartesian closed for the same reason.
- If G is a groupGroup (mathematics)In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
, then the category of all G-setsGroup actionIn algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
is cartesian closed. If Y and Z are two G-sets, then ZY is the set of all functions from Y to Z with G action defined by (g.F)(y) = g.(F(g-1.y)) for all g in G, F:Y → Z and y in Y. - The category of finite G-sets is also cartesian closed.
- The category Cat of all small categories (with functors as morphisms) is cartesian closed; the exponential CD is given by the functor categoryFunctor categoryIn category theory, a branch of mathematics, the functors between two given categories form a category, where the objects are the functors and the morphisms are natural transformations between the functors...
consisting of all functors from D to C, with natural transformationNatural transformationIn category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Indeed this intuition...
s as morphisms. - If C is a small category, then the functor categoryFunctor categoryIn category theory, a branch of mathematics, the functors between two given categories form a category, where the objects are the functors and the morphisms are natural transformations between the functors...
SetC consisting of all covariant functors from C into the category of sets, with natural transformationNatural transformationIn category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Indeed this intuition...
s as morphisms, is cartesian closed. If F and G are two functors from C to Set, then the exponential FG is the functor whose value on the object X of C is given by the set of all natural transformations from (X,−) × G to F.- The earlier example of G-sets can be seen as a special case of functor categories: every group can be considered as a one-object category, and G-sets are nothing but functors from this category to Set
- The category of all directed graphsGraph theoryIn mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
is cartesian closed; this is a functor category as explained under functor categoryFunctor categoryIn category theory, a branch of mathematics, the functors between two given categories form a category, where the objects are the functors and the morphisms are natural transformations between the functors...
.
- In algebraic topologyAlgebraic topologyAlgebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
, cartesian closed categories are particularly easy to work with. Neither the category of topological spaceTopological spaceTopological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s with continuous maps nor the category of smooth manifoldsManifoldIn mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
with smooth maps is cartesian closed. Substitute categories have therefore been considered: the category of compactly generated Hausdorff spaces is cartesian closed, as is the category of Frölicher spaceFrölicher spaceIn mathematics, Frölicher spaces extend the notions of calculus and smooth manifolds. They were introduced in 1982 by the mathematician Alfred Frölicher.-Definition:...
s. - In order theoryOrder theoryOrder theory is a branch of mathematics which investigates our intuitive notion of order using binary relations. It provides a formal framework for describing statements such as "this is less than that" or "this precedes that". This article introduces the field and gives some basic definitions...
, complete partial orderComplete partial orderIn mathematics, directed complete partial orders and ω-complete partial orders are special classes of partially ordered sets, characterized by particular completeness properties...
s (cpos) have a natural topology, the Scott topology, whose continuous maps do form a cartesian closed category (that is, the objects are the cpos, and the morphisms are the Scott continuous maps). Both curryingCurryingIn mathematics and computer science, currying is the technique of transforming a function that takes multiple arguments in such a way that it can be called as a chain of functions each with a single argument...
and applyApplyIn mathematics and computer science, Apply is a function that applies functions to arguments. It is central to programming languages derived from lambda calculus, such as LISP and Scheme, and also in functional languages...
are continuous functions in the Scott topology, and currying, together with apply, provide the adjoint. - A Heyting algebraHeyting algebraIn mathematics, a Heyting algebra, named after Arend Heyting, is a bounded lattice equipped with a binary operation a→b of implication such that ∧a ≤ b, and moreover a→b is the greatest such in the sense that if c∧a ≤ b then c ≤ a→b...
is a Cartesian closed (bounded) latticeLattice (order)In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
. An important example arises from topological spaceTopological spaceTopological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s. If X is a topological spaceTopological spaceTopological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
, then the open setOpen setThe concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
s in X form the objects of a category O(X) for which there is a unique morphism from U to V if U is a subset of V and no morphism otherwise. This poset is a cartesian closed category: the "product" of U and V is the intersection of U and V and the exponential UV is the interiorInterior (topology)In mathematics, specifically in topology, the interior of a set S of points of a topological space consists of all points of S that do not belong to the boundary of S. A point that is in the interior of S is an interior point of S....
of U∪(X\V).
The following categories are not cartesian closed:
- The category of all vector spaceVector spaceA vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s over some fixed fieldField (mathematics)In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
is not cartesian closed; neither is the category of all finite-dimensional vector spaces. While they have products (called direct sums), the product functors do not have right adjoints. (They are, however, symmetric monoidal closed categories: the set of linear transformations between two vector spaces forms another vector space, so they are closed, and if one replaces the product by the tensor productTensor productIn mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
, a similar isomorphism exists between the Hom spaces.) - The category of abelian groupAbelian groupIn abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s is not cartesian closed, for the same reason.
Applications
In cartesian closed categories, a "function of two variables" (a morphism f:X×Y → Z) can always be represented as a "function of one variable" (the morphism λf:X → ZY). In computer scienceComputer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
applications, this is known as currying
Currying
In mathematics and computer science, currying is the technique of transforming a function that takes multiple arguments in such a way that it can be called as a chain of functions each with a single argument...
; it has led to the realization that simply-typed lambda calculus can be interpreted in any cartesian closed category.
The Curry-Howard-Lambek correspondence provides a deep isomorphism between intuitionistic logic, simply-typed lambda calculus and cartesian closed categories.
Certain cartesian closed categories, the topoi
Topos
In mathematics, a topos is a type of category that behaves like the category of sheaves of sets on a topological space...
, have been proposed as a general setting for mathematics, instead of traditional set theory
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
.
The renowned computer scientist John Backus
John Backus
John Warner Backus was an American computer scientist. He directed the team that invented the first widely used high-level programming language and was the inventor of the Backus-Naur form , the almost universally used notation to define formal language syntax.He also did research in...
has advocated a variable-free notation, or Function-level programming
Function-level programming
In computer science, function-level programming refers to one of the two contrasting programming paradigms identified by John Backus in his work on programs as mathematical objects, the other being value-level programming....
, which in retrospect bears some similarity to the internal language of cartesian closed categories. CAML is more consciously modelled on cartesian closed categories.
Equational theory
In every cartesian closed category (using exponential notation), (XY)Z and (XZ)Y are isomorphic for all objects X, Y and Z. We write this as the "equation"z = (xz)y.
One may ask what other such equations are valid in all cartesian closed categories. It turns out that all of them follow logically from the following axioms:
- x×(y×z) = (x×y)×z
- x×y = y×x
- x×1 = x (here 1 denotes the terminal object of C)
- 1x = 1
- x1 = x
- (x×y)z = xz×yz
- (xy)z = x(y×z)
Bicartesian closed categories extend cartesian closed categories with binary coproduct
Coproduct
In category theory, the coproduct, or categorical sum, is the category-theoretic construction which includes the disjoint union of sets and of topological spaces, the free product of groups, and the direct sum of modules and vector spaces. The coproduct of a family of objects is essentially the...
s and an initial object
Initial object
In category theory, an abstract branch of mathematics, an initial object of a category C is an object I in C such that for every object X in C, there exists precisely one morphism I → X...
, with products distributing over coproducts. Their equational theory is extended with the following axioms:
- x + y = y + x
- (x + y) + z = x + (y + z)
- x(y + z) = xy + xz
- x(y + z) = xyxz
- 0 + x = x
- x×0 = 0
- x0 = 1

