A quantity is said to be subject to exponential decay if it decreases at a rate proportional to its value. Symbolically, this process can be expressed by the following differential equation

Differential equation

A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...

, where N is the quantity and λ (lambda) is a positive number called the decay constant:


The solution to this equation (see derivation below) is:
Exponential rate of change

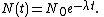
Here N(t) is the quantity at time t, and N₀ = N(0) is the initial quantity, i.e.