
Simple extension
Encyclopedia
In mathematics
, more specifically in field theory
, a simple extension is a field extension
which is generated by the adjunction
of a single element. Simple extensions are well understood and can be completely classified.
The primitive element theorem
provides a characterization of the finite extensions which are simple.
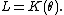
The element θ is called a primitive element, or generating element, for the extension; we also say that L is generated over K by θ.
A primitive element of a finite field
is a generator
of the field's multiplicative group. When said at greater length: In the realm of finite field
s, a stricter definition of primitive element is used. The multiplicative group of a finite field is cyclic
, and an element is called a primitive element if and only if it is a generator
for the multiplicative group. The distinction is that the earlier definition requires that every element of the field be a quotient of polynomials in the primitive element, but within the realm of finite fields the requirement is that every nonzero element be a pure power of a primitive element. An attempt to distinguish these meanings by calling θ a field primitive element of L over K, and a generator of the multiplicative group of a finite field a group primitive element is made by .
K[X] in one indeterminate,
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, more specifically in field theory
Field theory (mathematics)
Field theory is a branch of mathematics which studies the properties of fields. A field is a mathematical entity for which addition, subtraction, multiplication and division are well-defined....
, a simple extension is a field extension
Field extension
In abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
which is generated by the adjunction
Adjunction (field theory)
In abstract algebra, adjunction is a construction in field theory, where for a given field extension E/F, subextensions between E and F are constructed.- Definition :...
of a single element. Simple extensions are well understood and can be completely classified.
The primitive element theorem
Primitive element theorem
In mathematics, more specifically in the area of modern algebra known as field theory, the primitive element theorem or Artin's theorem on primitive elements is a result characterizing the finite degree field extensions that possess a primitive element...
provides a characterization of the finite extensions which are simple.
Definition
A field extension L/K is called a simple extension if there exists an element θ in L with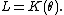
The element θ is called a primitive element, or generating element, for the extension; we also say that L is generated over K by θ.
A primitive element of a finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
is a generator
Generating set of a group
In abstract algebra, a generating set of a group is a subset that is not contained in any proper subgroup of the group. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination of finitely many elements of the subset and their...
of the field's multiplicative group. When said at greater length: In the realm of finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
s, a stricter definition of primitive element is used. The multiplicative group of a finite field is cyclic
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
, and an element is called a primitive element if and only if it is a generator
Generating set of a group
In abstract algebra, a generating set of a group is a subset that is not contained in any proper subgroup of the group. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination of finitely many elements of the subset and their...
for the multiplicative group. The distinction is that the earlier definition requires that every element of the field be a quotient of polynomials in the primitive element, but within the realm of finite fields the requirement is that every nonzero element be a pure power of a primitive element. An attempt to distinguish these meanings by calling θ a field primitive element of L over K, and a generator of the multiplicative group of a finite field a group primitive element is made by .
Examples
- C:R (generated by i)
- Q(√2):Q (generated by √2), more generally any number field is a simple extension Q(α) for some α
- F(X):F (generated by X).
Classification of simple extensions
Given a field K the simple extensions K(θ) can be completely classified using the polynomial ringPolynomial ring
In mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
K[X] in one indeterminate,
- Let K(θ) be a simple extension. If θ is algebraicAlgebraic elementIn mathematics, if L is a field extension of K, then an element a of L is called an algebraic element over K, or just algebraic over K, if there exists some non-zero polynomial g with coefficients in K such that g=0...
over K then K(θ) is identical to K[θ]. If θ is transcendental over K then K(θ) is isomorphic to the field of fractionsField of fractionsIn abstract algebra, the field of fractions or field of quotients of an integral domain is the smallest field in which it can be embedded. The elements of the field of fractions of the integral domain R have the form a/b with a and b in R and b ≠ 0...
of K[X].

