
Global field
Encyclopedia
In mathematics
, the term global field refers to either of the following:
An axiomatic characterization of these fields via valuation theory was given by Emil Artin
and George Whaples in the 1940s.
There are a number of formal similarities between the two kinds of fields. A field of either type has the property that all of its completion
s are locally compact fields (see local field
s). Every field of either type can be realized as the field of fractions
of a Dedekind domain
in which every non-zero ideal
is of finite index. In each case, one has the product formula for non-zero elements x: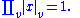
The analogy between the two kinds of fields has been a strong motivating force in algebraic number theory
. The idea of an analogy between number fields and Riemann surface
s goes back to Richard Dedekind
and Heinrich M. Weber in the nineteenth century. The more strict analogy expressed by the 'global field' idea, in which a Riemann surface's aspect as algebraic curve is mapped to curves defined over a finite field, was built up during the 1930s, culminating in the Riemann hypothesis for local zeta-functions settled by André Weil
in 1940. The terminology may be due to Weil, who wrote his Basic Number Theory (1967) in part to work out the parallelism.
It is usually easier to work in the function field case and then try to develop parallel techniques on the number field side. The development of Arakelov theory
and its exploitation by Gerd Faltings
in his proof of the Mordell conjecture is a dramatic example.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the term global field refers to either of the following:
- an algebraic number fieldAlgebraic number fieldIn mathematics, an algebraic number field F is a finite field extension of the field of rational numbers Q...
, i.e., a finite extensionAlgebraic extensionIn abstract algebra, a field extension L/K is called algebraic if every element of L is algebraic over K, i.e. if every element of L is a root of some non-zero polynomial with coefficients in K. Field extensions that are not algebraic, i.e...
of Q, or - a global function field, i.e., the function fieldFunction field of an algebraic varietyIn algebraic geometry, the function field of an algebraic variety V consists of objects which are interpreted as rational functions on V...
of an algebraic curveAlgebraic curveIn algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...
over a finite fieldFinite fieldIn abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
, equivalently, a finite extension of Fq(T), the field of rational functions in one variable over the finite field with q elements.
An axiomatic characterization of these fields via valuation theory was given by Emil Artin
Emil Artin
Emil Artin was an Austrian-American mathematician of Armenian descent.-Parents:Emil Artin was born in Vienna to parents Emma Maria, née Laura , a soubrette on the operetta stages of Austria and Germany, and Emil Hadochadus Maria Artin, Austrian-born of Armenian descent...
and George Whaples in the 1940s.
There are a number of formal similarities between the two kinds of fields. A field of either type has the property that all of its completion
Complete space
In mathematical analysis, a metric space M is called complete if every Cauchy sequence of points in M has a limit that is also in M or, alternatively, if every Cauchy sequence in M converges in M....
s are locally compact fields (see local field
Local field
In mathematics, a local field is a special type of field that is a locally compact topological field with respect to a non-discrete topology.Given such a field, an absolute value can be defined on it. There are two basic types of local field: those in which the absolute value is archimedean and...
s). Every field of either type can be realized as the field of fractions
Field of fractions
In abstract algebra, the field of fractions or field of quotients of an integral domain is the smallest field in which it can be embedded. The elements of the field of fractions of the integral domain R have the form a/b with a and b in R and b ≠ 0...
of a Dedekind domain
Dedekind domain
In abstract algebra, a Dedekind domain or Dedekind ring, named after Richard Dedekind, is an integral domain in which every nonzero proper ideal factors into a product of prime ideals. It can be shown that such a factorization is then necessarily unique up to the order of the factors...
in which every non-zero ideal
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
is of finite index. In each case, one has the product formula for non-zero elements x:
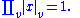
The analogy between the two kinds of fields has been a strong motivating force in algebraic number theory
Algebraic number theory
Algebraic number theory is a major branch of number theory which studies algebraic structures related to algebraic integers. This is generally accomplished by considering a ring of algebraic integers O in an algebraic number field K/Q, and studying their algebraic properties such as factorization,...
. The idea of an analogy between number fields and Riemann surface
Riemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
s goes back to Richard Dedekind
Richard Dedekind
Julius Wilhelm Richard Dedekind was a German mathematician who did important work in abstract algebra , algebraic number theory and the foundations of the real numbers.-Life:...
and Heinrich M. Weber in the nineteenth century. The more strict analogy expressed by the 'global field' idea, in which a Riemann surface's aspect as algebraic curve is mapped to curves defined over a finite field, was built up during the 1930s, culminating in the Riemann hypothesis for local zeta-functions settled by André Weil
André Weil
André Weil was an influential mathematician of the 20th century, renowned for the breadth and quality of his research output, its influence on future work, and the elegance of his exposition. He is especially known for his foundational work in number theory and algebraic geometry...
in 1940. The terminology may be due to Weil, who wrote his Basic Number Theory (1967) in part to work out the parallelism.
It is usually easier to work in the function field case and then try to develop parallel techniques on the number field side. The development of Arakelov theory
Arakelov theory
Arakelov theory is an approach to Diophantine geometry, named for Suren Arakelov. It is used to study Diophantine equations in higher dimensions.-Background:...
and its exploitation by Gerd Faltings
Gerd Faltings
Gerd Faltings is a German mathematician known for his work in arithmetic algebraic geometry.From 1972 to 1978, he studied mathematics and physics at the University of Münster. In 1978 he received his PhD in mathematics and in 1981 he got the venia legendi in mathematics, both from the University...
in his proof of the Mordell conjecture is a dramatic example.

