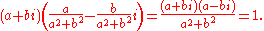Algebraic number field
Encyclopedia
In mathematics
, an algebraic number field (or simply number field) F is a finite (and hence algebraic
) field extension
of the field
of rational number
s Q. Thus F is a field that contains Q and has finite dimension when considered as a vector space
over Q.
The study of algebraic number fields, and, more generally, of algebraic extensions of the field of rational numbers, is the central topic of algebraic number theory
.
. Fields consists of a set of elements together with four operations, namely addition
, subtraction
, multiplication
and division
by nonzero elements. A prominent example of a field is the field of rational number
s, commonly denoted Q, together with its usual operations of addition etc.
Another notion needed to define algebraic number fields is vector space
s. To the extent needed here, vector spaces can be thought of as consisting of sequences (or tuple
s)
whose entries are elements of a fixed field, such as the field Q. Any two such sequences can be added by adding the entries one per one. In addition, any sequence can be multiplied by a single element c of the fixed field. These two operations known as vector addition and scalar multiplication
satisfy a number of properties that serve to define vector spaces abstractly. Vector spaces are allowed to be "infinite-dimensional", that is to say that the sequences constituting the vector spaces are of infinite length. If, however, the vector space consists of finite sequences,
the vector space is said to be of finite dimension, n.
field extension
of the field of rational numbers. Its degree as an extension of Q is simply called its degree.
· (0, 1) = (1 · 0, 0 · 1) = (0, 0).
, a field extension F / E is algebraic if every element f of the bigger field F is the zero of a polynomial
with coefficients e0, ..., em in E:
It is a fact that every finite field extension is algebraic (proof: for x in F simply consider x, x^2, x^3 ...we get a linear dependence, i.e. a polynomial x is a root of!). In particular this applies to algebraic number fields, so any element f of an algebraic number field F can be written as a zero of a polynomial with rational coefficients. Therefore, elements of F are also referred to as algebraic numbers. Given a polynomial p such that p(f) = 0, it can be arranged such that the leading coefficient em is one, by dividing all coefficients by it, if necessary. A polynomial with this property is known as a monic polynomial. In general it will have rational coefficients. If, however, its coefficients are actually all integers, f is called an algebraic integer
. Any (usual) integer z ∈ Z is an algebraic integer, as it is the zero of the linear monic polynomial:
It can be shown that any algebraic integer that is also a rational number must actually be an integer, whence the name "algebraic integer". Again using abstract algebra, specifically the notion of a finitely generated module, it can be shown that the sum and the product of any two algebraic integers is still an algebraic integer, it follows that the algebraic integers in F form a ring
denoted OF called the ring of integers of F. It is a subring
of (that is, a ring contained in) F. A field contains no zero divisors and this property is inherited by any subring. Therefore, the ring of integers of F is an integral domain. The field F is the field of fractions
of the integral domain OF. This way one can get back and forth between the algebraic number field F and its ring of integers OF. Rings of algebraic integers have three distinctive properties: firstly, OF is an integral domain that is integrally closed
in its field of fractions F. Secondly, OF is a Noetherian ring
. Finally, every nonzero prime ideal
of OF is maximal
or, equivalently, the Krull dimension
of this ring is one. An abstract commutative ring with these three properties is called a Dedekind ring (or Dedekind domain), in honor of Richard Dedekind
, who undertook a deep study of rings of algebraic integers.
into a product of prime ideal
s. However, unlike Z as the ring of integers of Q, the ring of integers of a proper extension of Q need not admit unique factorization
of numbers into a product of prime numbers or, more precisely, prime element
s. This happens already for quadratic integer
s, for example in OQ(√) = Z[√], the unicity of the factorization fails:
–using the norm it can be shown that these two factorization are actually inequivalent in the sense that the factors do not just differ by a unit
in OQ(√). Euclidean domain
s are unique factorization domains; for example Z[i], the ring of Gaussian integer
s, and Z[ω], the ring of Eisenstein integer
s, where ω is a third root of unity (unequal to 1), have this property.
. This group is always finite. The ring of integers OF possesses unique factorization if and only if it is a principal ring or, equivalently, if F has class number 1. Given a number field, the class number is often difficult to compute. The class number problem, going back to Gauss
, is concerned with the existence of imaginary quadratic number fields (i.e., Q(√), d ≥ 1) with prescribed class number. The class number formula
relates h to other fundamental invariants of F. It involves the Dedekind zeta function
ζF(s), a function in a complex variable s, defined by .
.
(The product is over all prime ideals of OF,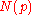 denotes the norm of the prime ideal or, equivalently, the (finite) number of elements in the residue field
denotes the norm of the prime ideal or, equivalently, the (finite) number of elements in the residue field
 . The infinite product converges only for Re(s) > 1, in general analytic continuation
. The infinite product converges only for Re(s) > 1, in general analytic continuation
and the functional equation
for the zeta-function are needed to define the function for all s).
The Dedekind zeta-function generalizes the Riemann zeta-function in that ζQ(s) = ζ(s).
The class number formula states that ζF(s) has a simple pole at s = 1 and at this point (its meromorphic continuation to the whole complex plane) the residue
is given by
Here r1 and r2 classically denote the number of real embeddings and pairs of complex embeddings of F, respectively. Moreover, Reg is the regulator of F, w the number of roots of unity
in F and D is the discriminant of F.
Dirichlet L-functions L(χ, s) are a more refined variant of ζ(s). Both types of functions encode the arithmetic behavior of Q and F, respectively. For example, Dirichlet's theorem
asserts that in any arithmetic progression
with coprime
a and m, there are infinitely many prime numbers. This theorem is implied by the fact that the Dirichlet L-function is nonzero at s = 1. Using much more advanced techniques including algebraic K-theory
and Tamagawa measures, modern number theory deals with a description, if largely conjectural (see Tamagawa number conjecture), of values of more general L-function
s.
of n algebraic integers in F such that every element of the ring of integers OF of F can be written uniquely as a Z-linear combination of elements of B; that is, for any x in OF we have
where the mi are (ordinary) integers. It is then also the case that any element of F can be written uniquely as
where now the mi are rational numbers. The algebraic integers of F are then precisely those elements of F where the mi are all integers.
Working locally
and using tools such as the Frobenius map, it is always possible to explicitly compute such a basis, and it is now standard for computer algebra system
s to have built-in programs to do this.
for some element x ∈ F. By the primitive element theorem
, for there exists such an x, called a primitive element. If x can be chosen in OF and such that Bx is a basis of OF as a free Z-module, then Bx is called a power integral basis, and the field F is called a monogenic field
. An example of a number field that is not monogenic was first given by Dedekind. His example is the field obtained by adjoining a root of the polynomial .
by requiring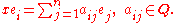
Here e1, ..., en is a fixed basis for F, viewed as a Q-vector space. The rational numbers aij are uniquely determined by x and the choice of a basis since any element of F can be uniquely represented as a linear combination
of the basis elements. This way of associating a matrix to any element of the field F is called the regular representation
. The square matrix A represents the effect of multiplication by x in the given basis. It follows that if the element y of F is represented by a matrix B, then the product xy is represented by the matrix product AB. Invariant
s of matrices, such as the trace
, determinant
, and characteristic polynomial
, depend solely on the field element x and not on the basis. In particular, the trace of the matrix A(x) is called the trace
of the field element x and denoted Tr(x), and the determinant is called the norm
of x and denoted N(x).
By definition, standard properties of traces and determinants of matrices carry over to Tr and N: Tr(x) is a linear function
of x, as expressed by Tr(x + y) = Tr(x) + Tr(y), Tr(λx) = λ Tr(x), and the norm is a multiplicative homogeneous function
of degree n: N(xy) = N(x) N(y), N(λx) = λn N(x). Here λ is a rational number, and x, y are any two elements of F.
The trace form derives is a bilinear form defined by means of the trace, as Tr(x y). The integral trace form, an integer-valued symmetric matrix is defined as tij = Tr(bibj), where b1, ..., bn is an integral basis for F. The discriminant
of F is defined as det(t). It is an integer, and is an invariant property of the field F, not depending on the choice of integral basis.
The matrix associated to an element x of F can also be used to give other, equivalent descriptions of algebraic integers. An element x of F is an algebraic integer if and only if the characteristic polynomial pA of the matrix A associated to x is a monic polynomial with integer coefficients. Suppose that the matrix A that represents an element x has integer entries in some basis e. By the Cayley–Hamilton theorem
, pA(A) = 0, and it follows that pA(x) = 0, so that x is an algebraic integer. Conversely, if x is an element of F which is a root of a monic polynomial with integer coefficients then the same property holds for the corresponding matrix A. In this case it can be proven that A is an integer matrix
in a suitable basis of F. Note that the property of being an algebraic integer is defined in a way that is independent of a choice of a basis in F.

The "3" in the upper left hand corner of this matrix is the trace of the matrix of the map defined by the first basis element (1) in the regular representation of F on F. This basis element induces the identity map on the 3-dimensional vector space, F. The trace of the matrix of the identity map on a 3-dimensional vector space is 3.
The determinant of this is 1304 = 23 163, the field discriminant; in comparison the root discriminant
, or discriminant of the polynomial, is 5216 = 25 163.
s by Hensel
in 1897; and now it is standard to consider all of the various possible embeddings of a number field F into its various topological completion
s at once.
A place of a number field F is an equivalence class of absolute values
on F. Essentially, an absolute value is a notion to measure the size of elements f of F. Two such absolute values are considered equivalent if they give rise to the same notion of smallness (or proximity). In general, they fall into three regimes. Firstly (and mostly irrelevant), the trivial absolute value | |0, which takes the value 1 on all non-zero f in F. The second and third classes are Archimedean places and non-Archimedean (or ultrametric) places. The completion of F with respect to a place is given in both cases by taking Cauchy sequence
s in F and dividing out null sequences, that is, sequences (xn)n ∈ N such that |xn| tends to zero when n tends to infinity. This can be shown to be a field again, the so-called completion of F at the given place.
For F = Q, the following non-trivial norms occur (Ostrowski's theorem
): the (usual) absolute value
, which gives rise to the complete topological field of the real numbers R. On the other hand, for any prime number p, the p-adic
absolute values is defined by
In contrast to the usual absolute value, the p-adic norm gets smaller when q is multiplied by p, leading to quite different behavior of Qp vis-à-vis R.
complex numbers, which allows for two conjugate embeddings into C. Either one of this pair of embeddings can be used to define an absolute value on F, which is the same for both embeddings since they are conjugate. This absolute value is called a complex place of F.
If all roots of f above are real or, equivalently, any embedding F ⊂ C is actually inside R, F is called totally real
.
behaves in many ways like a number field, and the p-adic numbers may similarly play the role of the rationals; in particular, we can define the norm and trace in exactly the same way, now giving functions mapping to Qp. By using this p-adic norm map Nt for the place t, we may define an absolute value corresponding to a given p-adically irreducible factor t of degree m by |θ|t = |Nt(θ)|p1/m. Such an absolute value is called an ultrametric, non-Archimedean or p-adic place of F.
For any ultrametric place v we have that |x|v ≤ 1 for any x in OF, since the minimal polynomial for x has integer factors, and hence its p-adic factorization has factors in Zp. Consequently, the norm term (constant term) for each factor is a p-adic integer, and one of these is the integer used for defining the absolute value for v.
P of OF. This relies on the ultrametricity of v: given x and y in P, then
Actually, P is even a prime ideal
.
Conversely, given a prime ideal P of OF, a discrete valuation can be defined by setting vP(x) = n where n is the biggest integer such that x ∈ Pn, the n-fold power of the ideal. This valuation can be turned into a ultrametic place. Under this correspondence, (equivalence classes) of ultrametric places of F correspond to prime ideals of OF. For F = Q, this gives back Ostrowski's theorem: any prime ideal in Z (which is necessarily by a single prime number) corresponds to an non-archimedean place and vice versa. However, for more general number fields, the situation becomes more involved, as will be explained below.
Yet another, equivalent way of describing ultrametric places is by means of localizations
of OF. Given an ultrametric place v on a number field F, the corresponding localization is the subring T of F of all elements x such that | x |v ≤ 1. By the ultrametric property T is a ring. Moreover, it contains OF. For every element x of F, at least one of x or x−1 is contained in T. Actually, since F×/T× can be shown to be isomorphic to the integers, T is a discrete valuation ring
, in particular a local ring
. Actually, T is just the localization of OF at the prime ideal P. Conversely, P is the maximal ideal of T.
Altogether, there is a three-way equivalence between ultrametric absolute values, prime ideals, and localizations on a number field.
 Ramification
Ramification
, generally speaking, describes a geometric phenomenon that can occur with finite-to-one maps (that is, maps f: X → Y such that the preimages of all points y in Y consist only of finitely many points): the cardinality of the fibers f−1(y) will generally have the same number of points, but it occurs that, in special points y, this number drops. For example, the map
has n points in each fiber over t, namely the n (complex) roots of t, except in t = 0, where the fiber consists of only one element, z = 0. One says that the map is "ramified" in zero. This is an example of a branched covering
of Riemann surface
s. This intuition also serves to define ramification in algebraic number theory
. Given a (necessarily finite) extension of number fields F / E, a prime ideal p of OE generates the ideal pOF of OF. This ideal may or may not be a prime ideal, but, according to the Lasker–Noether theorem (see above), always is given by
with uniquely determined prime ideals qi of OF and numbers (called ramification indices) ei. Whenever one ramification index is bigger than one, the prime p is said to ramify in F.
The connection between this definition and the geometric situation is delivered by the map of spectra
of rings Spec OF → Spec OE. In fact, unramified morphisms of scheme
s in algebraic geometry
are a direct generalization of unramified extensions of number fields.
Ramification is a purely local property, i.e., depends only on the completions around the primes p and qi. The inertia group measures the difference between the local Galois groups at some place and the Galois groups of the involved finite residue fields.
at 23, it suffices to consider the field extension Q23(x) / Q23. Up to 529 = 232 (i.e., modulo
529) f can be factored as
Substituting x = y + 10 in the first factor g modulo 529 yields y + 191, so the valuation | y |g for y given by g is | −191 |23 = 1. On the other hand the same substitution in h yields Since 161 = 7 × 23,
Since possible values for the absolute value of the place defined by the factor h are not confined to integer powers of 23, but instead are integer powers of the square root of 23, the ramification index of the field extension at 23 is two.
The valuations of any element of F can be computed in this way using resultants. If, for example y = x2 − x − 1, using the resultant to eliminate x between this relationship and f = x3 − x − 1 = 0 gives . If instead we eliminate with respect to the factors g and h of f, we obtain the corresponding factors for the polynomial for y, and then the 23-adic valuation applied to the constant (norm) term allows us to compute the valuations of y for g and h (which are both 1 in this instance.)
Gal(F / E), consisting of field automorphisms of F leaving E elementwise fixed. As an example, the Galois group Gal (Q(ζn) / Q) of the cyclotomic field extension of degree n (see above) is given by (Z/nZ)×, the group of invertible elements in Z/nZ. This is the first stepstone into Iwasawa theory
.
In order to include all possible extensions having certain properties, the Galois group concept is commonly applied to the (infinite) field extension / F of the algebraic closure
, leading to the absolute Galois group
G := Gal( / F) or just Gal(F), and to the extension F / Q. The fundamental theorem of Galois theory
links fields in between F and its algebraic closure and closed subgroups of Gal (F). For example, the abelianization (the biggest abelian quotient) Gab of G corresponds to a field referred to as the maximal abelian extension
Fab (called so since any further extension is not abelian, i.e., does not have an abelian Galois group). By the Kronecker–Weber theorem
, the maximal abelian extension of Q is the extension generated by all roots of unity. For more general number fields, class field theory
, specifically the Artin reciprocity law gives an answer by describing Gab in terms of the idele class group. Also notable is the Hilbert class field
, the maximal abelian unramified field extension of F. It can be shown to be finite over F, its Galois group over F is isomorphic to the class group of F, in particular its degree equals the class number h of F (see above).
In certain situations, the Galois group acts
on other mathematical objects, for example a group. Such a group is then also referred to as a Galois module. This enables the use of group cohomology
for the Galois group Gal(F), also known as Galois cohomology
, which in the first place measures the failure of exactness of taking Gal(F)-invariants, but offers deeper insights (and questions) as well. For example, the Galois group G of a field extension L / F acts on L×, the nonzero elements of L. This Galois module plays a significant role in many arithmetic dualities
, such as Poitou-Tate duality. The Brauer group
of F, originally conceived to classify division algebra
s over F, can be recast as a cohomology group, namely H2(Gal (F), ×).
reifies that idea in topology
and geometry
.
known as function fields
of algebraic curve
s over finite field
s. An example is Fp(T). They are similar in many respects, for example in that number rings are one-dimensional regular rings, as are the coordinate rings (the quotient fields of which is the function field in question) of curves. Therefore, both types of field are called global field
s. In accordance with the philosophy laid out above, they can be studied at a local level first, that is to say, by looking at the corresponding local field
s. For number fields F, the local fields are the completions of F at all places, including the archimedean ones (see local analysis
). For function fields, the local fields are completions of the local rings at all points of the curve for function fields.
Many results valid for function fields also hold, at least if reformulated properly, for number fields. However, the study of number fields often poses difficulties and phenomena not encountered in function fields. For example, in function fields, there is no dichotomy into non-archimedean and archimedean places. Nonetheless, function fields often serves as a source of intuition what should be expected in the number field case.
at the archimedean places and p-adic analysis
at the nonarchimedean places) can be used. This implication does not hold, however, for more general types of equations. However, the idea of passing from local data to global ones proves fruitful in class field theory, for example, where local class field theory is used to obtain global insights mentioned above. This is also related to the fact that the Galois groups of the completions Fv can be explicitly determined, whereas the Galois groups of global fields, even of Q are far less understood.
is set up. A multiplicative variant is referred to as ideles.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an algebraic number field (or simply number field) F is a finite (and hence algebraic
Algebraic extension
In abstract algebra, a field extension L/K is called algebraic if every element of L is algebraic over K, i.e. if every element of L is a root of some non-zero polynomial with coefficients in K. Field extensions that are not algebraic, i.e...
) field extension
Field extension
In abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
of the field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
of rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s Q. Thus F is a field that contains Q and has finite dimension when considered as a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
over Q.
The study of algebraic number fields, and, more generally, of algebraic extensions of the field of rational numbers, is the central topic of algebraic number theory
Algebraic number theory
Algebraic number theory is a major branch of number theory which studies algebraic structures related to algebraic integers. This is generally accomplished by considering a ring of algebraic integers O in an algebraic number field K/Q, and studying their algebraic properties such as factorization,...
.
Prerequisites
The notion of algebraic number field relies on the concept of a fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
. Fields consists of a set of elements together with four operations, namely addition
Addition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
, subtraction
Subtraction
In arithmetic, subtraction is one of the four basic binary operations; it is the inverse of addition, meaning that if we start with any number and add any number and then subtract the same number we added, we return to the number we started with...
, multiplication
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
and division
Division (mathematics)
right|thumb|200px|20 \div 4=5In mathematics, especially in elementary arithmetic, division is an arithmetic operation.Specifically, if c times b equals a, written:c \times b = a\,...
by nonzero elements. A prominent example of a field is the field of rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s, commonly denoted Q, together with its usual operations of addition etc.
Another notion needed to define algebraic number fields is vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s. To the extent needed here, vector spaces can be thought of as consisting of sequences (or tuple
Tuple
In mathematics and computer science, a tuple is an ordered list of elements. In set theory, an n-tuple is a sequence of n elements, where n is a positive integer. There is also one 0-tuple, an empty sequence. An n-tuple is defined inductively using the construction of an ordered pair...
s)
whose entries are elements of a fixed field, such as the field Q. Any two such sequences can be added by adding the entries one per one. In addition, any sequence can be multiplied by a single element c of the fixed field. These two operations known as vector addition and scalar multiplication
Scalar multiplication
In mathematics, scalar multiplication is one of the basic operations defining a vector space in linear algebra . In an intuitive geometrical context, scalar multiplication of a real Euclidean vector by a positive real number multiplies the magnitude of the vector without changing its direction...
satisfy a number of properties that serve to define vector spaces abstractly. Vector spaces are allowed to be "infinite-dimensional", that is to say that the sequences constituting the vector spaces are of infinite length. If, however, the vector space consists of finite sequences,
the vector space is said to be of finite dimension, n.
Definition
An algebraic number field (or simply number field) is a finite degreeDegree of a field extension
In mathematics, more specifically field theory, the degree of a field extension is a rough measure of the "size" of the extension. The concept plays an important role in many parts of mathematics, including algebra and number theory — indeed in any area where fields appear prominently.-...
field extension
Field extension
In abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
of the field of rational numbers. Its degree as an extension of Q is simply called its degree.
Examples
- The smallest and most basic number field is the field Q of rational numbers. Many properties of general number fields, such as unique factorization, are modelled after the properties of Q.
- The Gaussian rationalGaussian rationalIn mathematics, a Gaussian rational number is a complex number of the form p + qi, where p and q are both rational numbers....
s, denoted Q(i) (read as "Q adjoined i"), form the first nontrivial example of a number field. Its elements are expressions of the form
-
- a+bi
- where both a and b are rational numbers and i is the imaginary unitImaginary unitIn mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial . The imaginary unit is denoted by , , or the Greek...
. Such expressions may be added, subtracted, and multiplied according to the usual rules of arithmetic and then simplified using the identity
-
- i2 = −1.
- Explicitly,
-
- (a + bi) + (c + di) = (a + c) + (b + d)i,
- (a + bi) (c + di) = (ac − bd) + (ad + bc)i.
- Non-zero Gaussian rational numbers are invertible, which can be seen from the identity
- It follows that the Gaussian rationals form a number field which is two-dimensional as a vector space over Q.
- More generally, for any square-freeSquare-freeIn mathematics, an element r of a unique factorization domain R is called square-free if it is not divisible by a non-trivial square. That is, every s such that s^2\mid r is a unit of R....
integer d, the quadratic fieldQuadratic fieldIn algebraic number theory, a quadratic field is an algebraic number field K of degree two over Q. It is easy to show that the map d ↦ Q is a bijection from the set of all square-free integers d ≠ 0, 1 to the set of all quadratic fields...
-
- Q(√)
- is a number field obtained by adjoining the square root of d to the field of rational numbers. Arithmetic operations in this field are defined in analogy with the case of gaussian rational numbers, d = − 1.
- Cyclotomic fieldCyclotomic fieldIn number theory, a cyclotomic field is a number field obtained by adjoining a complex primitive root of unity to Q, the field of rational numbers...
-
- Q(ζn), ζn = exp (2πi / n)
- is a number field obtained from Q by adjoining a primitive nth root of unity ζn. This field contains all complex nth roots of unity and its dimension over Q is equal to φ(n), where φ is the Euler totient function.
- The real numberReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s, R, and the complex numberComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s, C, are fields which have infinite dimension as Q-vector spaces, hence, they are not number fields. This follows from the uncountability of R and C as sets, whereas every number field is necessarily countable.
- The set Q2 of ordered pairOrdered pairIn mathematics, an ordered pair is a pair of mathematical objects. In the ordered pair , the object a is called the first entry, and the object b the second entry of the pair...
s of rational numbers, with the entrywise addition and multiplication is a two-dimensional commutative algebra over Q. However, it is not a field, since it has zero divisorZero divisorIn abstract algebra, a nonzero element a of a ring is a left zero divisor if there exists a nonzero b such that ab = 0. Similarly, a nonzero element a of a ring is a right zero divisor if there exists a nonzero c such that ca = 0. An element that is both a left and a right zero divisor is simply...
s:
· (0, 1) = (1 · 0, 0 · 1) = (0, 0).
Algebraicity and ring of integers
Generally, in abstract algebraAbstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, a field extension F / E is algebraic if every element f of the bigger field F is the zero of a polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
with coefficients e0, ..., em in E:
- p(f) = emfm + em−1fm−1 + ... + e1f + e0 = 0.
It is a fact that every finite field extension is algebraic (proof: for x in F simply consider x, x^2, x^3 ...we get a linear dependence, i.e. a polynomial x is a root of!). In particular this applies to algebraic number fields, so any element f of an algebraic number field F can be written as a zero of a polynomial with rational coefficients. Therefore, elements of F are also referred to as algebraic numbers. Given a polynomial p such that p(f) = 0, it can be arranged such that the leading coefficient em is one, by dividing all coefficients by it, if necessary. A polynomial with this property is known as a monic polynomial. In general it will have rational coefficients. If, however, its coefficients are actually all integers, f is called an algebraic integer
Algebraic integer
In number theory, an algebraic integer is a complex number that is a root of some monic polynomial with coefficients in . The set of all algebraic integers is closed under addition and multiplication and therefore is a subring of complex numbers denoted by A...
. Any (usual) integer z ∈ Z is an algebraic integer, as it is the zero of the linear monic polynomial:
- p(t) = t − z.
It can be shown that any algebraic integer that is also a rational number must actually be an integer, whence the name "algebraic integer". Again using abstract algebra, specifically the notion of a finitely generated module, it can be shown that the sum and the product of any two algebraic integers is still an algebraic integer, it follows that the algebraic integers in F form a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
denoted OF called the ring of integers of F. It is a subring
Subring
In mathematics, a subring of R is a subset of a ring, is itself a ring with the restrictions of the binary operations of addition and multiplication of R, and which contains the multiplicative identity of R...
of (that is, a ring contained in) F. A field contains no zero divisors and this property is inherited by any subring. Therefore, the ring of integers of F is an integral domain. The field F is the field of fractions
Field of fractions
In abstract algebra, the field of fractions or field of quotients of an integral domain is the smallest field in which it can be embedded. The elements of the field of fractions of the integral domain R have the form a/b with a and b in R and b ≠ 0...
of the integral domain OF. This way one can get back and forth between the algebraic number field F and its ring of integers OF. Rings of algebraic integers have three distinctive properties: firstly, OF is an integral domain that is integrally closed
Integrally closed
In mathematics, more specifically in abstract algebra, the concept of integrally closed has two meanings, one for groups and one for rings. -Commutative rings:...
in its field of fractions F. Secondly, OF is a Noetherian ring
Noetherian ring
In mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element...
. Finally, every nonzero prime ideal
Prime ideal
In algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...
of OF is maximal
Maximal ideal
In mathematics, more specifically in ring theory, a maximal ideal is an ideal which is maximal amongst all proper ideals. In other words, I is a maximal ideal of a ring R if I is an ideal of R, I ≠ R, and whenever J is another ideal containing I as a subset, then either J = I or J = R...
or, equivalently, the Krull dimension
Krull dimension
In commutative algebra, the Krull dimension of a ring R, named after Wolfgang Krull , is the supremum of the number of strict inclusions in a chain of prime ideals. The Krull dimension need not be finite even for a Noetherian ring....
of this ring is one. An abstract commutative ring with these three properties is called a Dedekind ring (or Dedekind domain), in honor of Richard Dedekind
Richard Dedekind
Julius Wilhelm Richard Dedekind was a German mathematician who did important work in abstract algebra , algebraic number theory and the foundations of the real numbers.-Life:...
, who undertook a deep study of rings of algebraic integers.
Unique factorization and class number
For general Dedekind rings, in particular rings of integers, there is a unique factorization of idealsIdeal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
into a product of prime ideal
Prime ideal
In algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...
s. However, unlike Z as the ring of integers of Q, the ring of integers of a proper extension of Q need not admit unique factorization
Unique factorization domain
In mathematics, a unique factorization domain is, roughly speaking, a commutative ring in which every element, with special exceptions, can be uniquely written as a product of prime elements , analogous to the fundamental theorem of arithmetic for the integers...
of numbers into a product of prime numbers or, more precisely, prime element
Prime element
In abstract algebra, an element p of a commutative ring R is said to be prime if it is not zero, not a unit and whenever p divides ab for some a and b in R, then p divides a or p divides b...
s. This happens already for quadratic integer
Quadratic integer
In number theory, quadratic integers are a generalization of the rational integers to quadratic fields. Important examples include the Gaussian integers and the Eisenstein integers. Though they have been studied for more than a hundred years, many open problems remain.- Definition :Quadratic...
s, for example in OQ(√) = Z[√], the unicity of the factorization fails:
- 6 = 2 · 3 = (1 + √) · (1 − √),
–using the norm it can be shown that these two factorization are actually inequivalent in the sense that the factors do not just differ by a unit
Unit (ring theory)
In mathematics, an invertible element or a unit in a ring R refers to any element u that has an inverse element in the multiplicative monoid of R, i.e. such element v that...
in OQ(√). Euclidean domain
Euclidean domain
In mathematics, more specifically in abstract algebra and ring theory, a Euclidean domain is a ring that can be endowed with a certain structure – namely a Euclidean function, to be described in detail below – which allows a suitable generalization of the Euclidean algorithm...
s are unique factorization domains; for example Z[i], the ring of Gaussian integer
Gaussian integer
In number theory, a Gaussian integer is a complex number whose real and imaginary part are both integers. The Gaussian integers, with ordinary addition and multiplication of complex numbers, form an integral domain, usually written as Z[i]. The Gaussian integers are a special case of the quadratic...
s, and Z[ω], the ring of Eisenstein integer
Eisenstein integer
In mathematics, Eisenstein integers , also known as Eulerian integers , are complex numbers of the formz = a + b\omega \,\!where a and b are integers and...
s, where ω is a third root of unity (unequal to 1), have this property.
ζ-functions, L-functions and class number formula
The failure of unique factorization is measured by the class number, commonly denoted h, the cardinality of the so-called ideal class groupIdeal class group
In mathematics, the extent to which unique factorization fails in the ring of integers of an algebraic number field can be described by a certain group known as an ideal class group...
. This group is always finite. The ring of integers OF possesses unique factorization if and only if it is a principal ring or, equivalently, if F has class number 1. Given a number field, the class number is often difficult to compute. The class number problem, going back to Gauss
Gauss
Gauss may refer to:*Carl Friedrich Gauss, German mathematician and physicist*Gauss , a unit of magnetic flux density or magnetic induction*GAUSS , a software package*Gauss , a crater on the moon...
, is concerned with the existence of imaginary quadratic number fields (i.e., Q(√), d ≥ 1) with prescribed class number. The class number formula
Class number formula
In number theory, the class number formula relates many important invariants of a number field to a special value of its Dedekind zeta function-General statement of the class number formula:...
relates h to other fundamental invariants of F. It involves the Dedekind zeta function
Dedekind zeta function
In mathematics, the Dedekind zeta function of an algebraic number field K, generally denoted ζK, is a generalization of the Riemann zeta function—which is obtained by specializing to the case where K is the rational numbers Q...
ζF(s), a function in a complex variable s, defined by
 .
.(The product is over all prime ideals of OF,
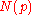 denotes the norm of the prime ideal or, equivalently, the (finite) number of elements in the residue field
denotes the norm of the prime ideal or, equivalently, the (finite) number of elements in the residue fieldResidue field
In mathematics, the residue field is a basic construction in commutative algebra. If R is a commutative ring and m is a maximal ideal, then the residue field is the quotient ring k = R/m, which is a field...
 . The infinite product converges only for Re(s) > 1, in general analytic continuation
. The infinite product converges only for Re(s) > 1, in general analytic continuationAnalytic continuation
In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which...
and the functional equation
Functional equation
In mathematics, a functional equation is any equation that specifies a function in implicit form.Often, the equation relates the value of a function at some point with its values at other points. For instance, properties of functions can be determined by considering the types of functional...
for the zeta-function are needed to define the function for all s).
The Dedekind zeta-function generalizes the Riemann zeta-function in that ζQ(s) = ζ(s).
The class number formula states that ζF(s) has a simple pole at s = 1 and at this point (its meromorphic continuation to the whole complex plane) the residue
Residue (complex analysis)
In mathematics, more specifically complex analysis, the residue is a complex number proportional to the contour integral of a meromorphic function along a path enclosing one of its singularities...
is given by

Here r1 and r2 classically denote the number of real embeddings and pairs of complex embeddings of F, respectively. Moreover, Reg is the regulator of F, w the number of roots of unity
Root of unity
In mathematics, a root of unity, or de Moivre number, is any complex number that equals 1 when raised to some integer power n. Roots of unity are used in many branches of mathematics, and are especially important in number theory, the theory of group characters, field theory, and the discrete...
in F and D is the discriminant of F.
Dirichlet L-functions L(χ, s) are a more refined variant of ζ(s). Both types of functions encode the arithmetic behavior of Q and F, respectively. For example, Dirichlet's theorem
Dirichlet's theorem on arithmetic progressions
In number theory, Dirichlet's theorem, also called the Dirichlet prime number theorem, states that for any two positive coprime integers a and d, there are infinitely many primes of the form a + nd, where n ≥ 0. In other words, there are infinitely many primes which are...
asserts that in any arithmetic progression
Arithmetic progression
In mathematics, an arithmetic progression or arithmetic sequence is a sequence of numbers such that the difference between the consecutive terms is constant...
- a, a + m, a + 2m, ...
with coprime
Coprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
a and m, there are infinitely many prime numbers. This theorem is implied by the fact that the Dirichlet L-function is nonzero at s = 1. Using much more advanced techniques including algebraic K-theory
Algebraic K-theory
In mathematics, algebraic K-theory is an important part of homological algebra concerned with defining and applying a sequenceof functors from rings to abelian groups, for all integers n....
and Tamagawa measures, modern number theory deals with a description, if largely conjectural (see Tamagawa number conjecture), of values of more general L-function
L-function
The theory of L-functions has become a very substantial, and still largely conjectural, part of contemporary analytic number theory. In it, broad generalisations of the Riemann zeta function and the L-series for a Dirichlet character are constructed, and their general properties, in most cases...
s.
Integral basis
An integral basis for a number field F of degree n is a set- B = {b1, …, bn}
of n algebraic integers in F such that every element of the ring of integers OF of F can be written uniquely as a Z-linear combination of elements of B; that is, for any x in OF we have
- x = m1b1 + … + mnbn,
where the mi are (ordinary) integers. It is then also the case that any element of F can be written uniquely as
- m1b1 + … + mnbn,
where now the mi are rational numbers. The algebraic integers of F are then precisely those elements of F where the mi are all integers.
Working locally
Local ring
In abstract algebra, more particularly in ring theory, local rings are certain rings that are comparatively simple, and serve to describe what is called "local behaviour", in the sense of functions defined on varieties or manifolds, or of algebraic number fields examined at a particular place, or...
and using tools such as the Frobenius map, it is always possible to explicitly compute such a basis, and it is now standard for computer algebra system
Computer algebra system
A computer algebra system is a software program that facilitates symbolic mathematics. The core functionality of a CAS is manipulation of mathematical expressions in symbolic form.-Symbolic manipulations:...
s to have built-in programs to do this.
Power basis
Let F be a number field of degree n. Among all possible bases of F (seen as a Q-vector space), there are particular ones known as power bases, that are bases of the form- Bx = {1, x, x2, ..., xn−1}
for some element x ∈ F. By the primitive element theorem
Primitive element theorem
In mathematics, more specifically in the area of modern algebra known as field theory, the primitive element theorem or Artin's theorem on primitive elements is a result characterizing the finite degree field extensions that possess a primitive element...
, for there exists such an x, called a primitive element. If x can be chosen in OF and such that Bx is a basis of OF as a free Z-module, then Bx is called a power integral basis, and the field F is called a monogenic field
Monogenic field
In mathematics, a monogenic field is an algebraic number field K for which there exists an element a such that the ring of integers OK is the polynomial ring Z[a]...
. An example of a number field that is not monogenic was first given by Dedekind. His example is the field obtained by adjoining a root of the polynomial .
The regular representation, trace and determinant
Using the multiplication in F, the elements of the field F may be represented by n-by-n matrices- A = A(x)=(aij)1 ≤ i, j ≤ n,
by requiring
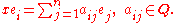
Here e1, ..., en is a fixed basis for F, viewed as a Q-vector space. The rational numbers aij are uniquely determined by x and the choice of a basis since any element of F can be uniquely represented as a linear combination
Linear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
of the basis elements. This way of associating a matrix to any element of the field F is called the regular representation
Regular representation
In mathematics, and in particular the theory of group representations, the regular representation of a group G is the linear representation afforded by the group action of G on itself by translation....
. The square matrix A represents the effect of multiplication by x in the given basis. It follows that if the element y of F is represented by a matrix B, then the product xy is represented by the matrix product AB. Invariant
Invariant (mathematics)
In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
s of matrices, such as the trace
Trace (linear algebra)
In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
, determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
, and characteristic polynomial
Characteristic polynomial
In linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....
, depend solely on the field element x and not on the basis. In particular, the trace of the matrix A(x) is called the trace
Field trace
In mathematics, the field trace is a function defined with respect to a finite field extension L/K. It is a K-linear map from L to K...
of the field element x and denoted Tr(x), and the determinant is called the norm
Field norm
In mathematics, the norm is a mapping defined in field theory, to map elements of a larger field into a smaller one.-Formal definitions:1. Let K be a field and L a finite extension of K...
of x and denoted N(x).
By definition, standard properties of traces and determinants of matrices carry over to Tr and N: Tr(x) is a linear function
Linear function
In mathematics, the term linear function can refer to either of two different but related concepts:* a first-degree polynomial function of one variable;* a map between two vector spaces that preserves vector addition and scalar multiplication....
of x, as expressed by Tr(x + y) = Tr(x) + Tr(y), Tr(λx) = λ Tr(x), and the norm is a multiplicative homogeneous function
Homogeneous function
In mathematics, a homogeneous function is a function with multiplicative scaling behaviour: if the argument is multiplied by a factor, then the result is multiplied by some power of this factor. More precisely, if is a function between two vector spaces over a field F, and k is an integer, then...
of degree n: N(xy) = N(x) N(y), N(λx) = λn N(x). Here λ is a rational number, and x, y are any two elements of F.
The trace form derives is a bilinear form defined by means of the trace, as Tr(x y). The integral trace form, an integer-valued symmetric matrix is defined as tij = Tr(bibj), where b1, ..., bn is an integral basis for F. The discriminant
Discriminant of an algebraic number field
In mathematics, the discriminant of an algebraic number field is a numerical invariant that, loosely speaking, measures the size of the algebraic number field...
of F is defined as det(t). It is an integer, and is an invariant property of the field F, not depending on the choice of integral basis.
The matrix associated to an element x of F can also be used to give other, equivalent descriptions of algebraic integers. An element x of F is an algebraic integer if and only if the characteristic polynomial pA of the matrix A associated to x is a monic polynomial with integer coefficients. Suppose that the matrix A that represents an element x has integer entries in some basis e. By the Cayley–Hamilton theorem
Cayley–Hamilton theorem
In linear algebra, the Cayley–Hamilton theorem states that every square matrix over a commutative ring satisfies its own characteristic equation....
, pA(A) = 0, and it follows that pA(x) = 0, so that x is an algebraic integer. Conversely, if x is an element of F which is a root of a monic polynomial with integer coefficients then the same property holds for the corresponding matrix A. In this case it can be proven that A is an integer matrix
Integer matrix
In mathematics, an integer matrix is a matrix whose entries are all integers. Examples include binary matrices, the zero matrix, the unit matrix, and the adjacency matrices used in graph theory, amongst many others...
in a suitable basis of F. Note that the property of being an algebraic integer is defined in a way that is independent of a choice of a basis in F.
Example
Consider F = Q(x), where x satisfies x3 − 11x2 + x + 1 = 0. Then an integral basis is [1, x, 1/2(x2 + 1)], and the corresponding integral trace form is
The "3" in the upper left hand corner of this matrix is the trace of the matrix of the map defined by the first basis element (1) in the regular representation of F on F. This basis element induces the identity map on the 3-dimensional vector space, F. The trace of the matrix of the identity map on a 3-dimensional vector space is 3.
The determinant of this is 1304 = 23 163, the field discriminant; in comparison the root discriminant
Discriminant
In algebra, the discriminant of a polynomial is an expression which gives information about the nature of the polynomial's roots. For example, the discriminant of the quadratic polynomialax^2+bx+c\,is\Delta = \,b^2-4ac....
, or discriminant of the polynomial, is 5216 = 25 163.
Places
Mathematicians of the nineteenth century assumed that algebraic numbers were a type of complex number. This situation changed with the discovery of p-adic numberP-adic number
In mathematics, and chiefly number theory, the p-adic number system for any prime number p extends the ordinary arithmetic of the rational numbers in a way different from the extension of the rational number system to the real and complex number systems...
s by Hensel
Kurt Hensel
Kurt Wilhelm Sebastian Hensel was a German mathematician born in Königsberg, Prussia.He was the son of the landowner and entrepreneur Sebastian Hensel, brother of the philosopher Paul Hensel, grandson of the composer Fanny Mendelssohn and the painter Wilhelm Hensel, and a descendant of the...
in 1897; and now it is standard to consider all of the various possible embeddings of a number field F into its various topological completion
Completion (ring theory)
In abstract algebra, a completion is any of several related functors on rings and modules that result in complete topological rings and modules. Completion is similar to localization, and together they are among the most basic tools in analysing commutative rings. Complete commutative rings have...
s at once.
A place of a number field F is an equivalence class of absolute values
Absolute value (algebra)
In mathematics, an absolute value is a function which measures the "size" of elements in a field or integral domain. More precisely, if D is an integral domain, then an absolute value is any mapping | x | from D to the real numbers R satisfying:* | x | ≥ 0,*...
on F. Essentially, an absolute value is a notion to measure the size of elements f of F. Two such absolute values are considered equivalent if they give rise to the same notion of smallness (or proximity). In general, they fall into three regimes. Firstly (and mostly irrelevant), the trivial absolute value | |0, which takes the value 1 on all non-zero f in F. The second and third classes are Archimedean places and non-Archimedean (or ultrametric) places. The completion of F with respect to a place is given in both cases by taking Cauchy sequence
Cauchy sequence
In mathematics, a Cauchy sequence , named after Augustin-Louis Cauchy, is a sequence whose elements become arbitrarily close to each other as the sequence progresses...
s in F and dividing out null sequences, that is, sequences (xn)n ∈ N such that |xn| tends to zero when n tends to infinity. This can be shown to be a field again, the so-called completion of F at the given place.
For F = Q, the following non-trivial norms occur (Ostrowski's theorem
Ostrowski's theorem
Ostrowski's theorem, due to Alexander Ostrowski , states that any non-trivial absolute value on the rational numbers Q is equivalent to either the usual real absolute value or a p-adic absolute value.- Definitions :...
): the (usual) absolute value
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
, which gives rise to the complete topological field of the real numbers R. On the other hand, for any prime number p, the p-adic
P-adic number
In mathematics, and chiefly number theory, the p-adic number system for any prime number p extends the ordinary arithmetic of the rational numbers in a way different from the extension of the rational number system to the real and complex number systems...
absolute values is defined by
- |q|p = p−n, where q = pn a/b and a and b are integers not divisible by p.
In contrast to the usual absolute value, the p-adic norm gets smaller when q is multiplied by p, leading to quite different behavior of Qp vis-à-vis R.
Archimedean places
Calculating the archimedean places of F is done as follows: let x be a primitive element of F, with minimal polynomial (over Q) f. Over R, f will generally no longer be irreducible, but its irreducible (real) factors are either of degree one or two. Since there are no repeated roots, there are no repeated factors. The roots r of factors of degree one are necessarily real, and replacing x by r gives an embedding of F into R; the number of such embeddings is equal to the number of real roots of f. Restricting the standard absolute value on R to F gives an archimedean absolute value on F; such an absolute value is also referred to as a real place of F. On the other hand, the roots of factors of degree two are pairs of conjugateComplex conjugate
In mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...
complex numbers, which allows for two conjugate embeddings into C. Either one of this pair of embeddings can be used to define an absolute value on F, which is the same for both embeddings since they are conjugate. This absolute value is called a complex place of F.
If all roots of f above are real or, equivalently, any embedding F ⊂ C is actually inside R, F is called totally real
Totally real number field
In number theory, a number field K is called totally real if for each embedding of K into the complex numbers the image lies inside the real numbers...
.
Nonarchimedian or ultrametric places
To find the nonarchimedean places, let again f and x be as above. In Qp, f splits in factors of various degrees, none of which are repeated, and the degrees of which add up to n, the degree of f. For each of these p-adically irreducible factors t, we may suppose that x satisfies t and obtain an embedding of F into an algebraic extension of finite degree over Qp. Such a local fieldLocal field
In mathematics, a local field is a special type of field that is a locally compact topological field with respect to a non-discrete topology.Given such a field, an absolute value can be defined on it. There are two basic types of local field: those in which the absolute value is archimedean and...
behaves in many ways like a number field, and the p-adic numbers may similarly play the role of the rationals; in particular, we can define the norm and trace in exactly the same way, now giving functions mapping to Qp. By using this p-adic norm map Nt for the place t, we may define an absolute value corresponding to a given p-adically irreducible factor t of degree m by |θ|t = |Nt(θ)|p1/m. Such an absolute value is called an ultrametric, non-Archimedean or p-adic place of F.
For any ultrametric place v we have that |x|v ≤ 1 for any x in OF, since the minimal polynomial for x has integer factors, and hence its p-adic factorization has factors in Zp. Consequently, the norm term (constant term) for each factor is a p-adic integer, and one of these is the integer used for defining the absolute value for v.
Prime ideals in OF
For an ultrametric place v, the subset of OF defined by |x|v < 1 is an idealIdeal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
P of OF. This relies on the ultrametricity of v: given x and y in P, then
- |x + y|v ≤ max (|x|v, |y|v) < 1.
Actually, P is even a prime ideal
Prime ideal
In algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...
.
Conversely, given a prime ideal P of OF, a discrete valuation can be defined by setting vP(x) = n where n is the biggest integer such that x ∈ Pn, the n-fold power of the ideal. This valuation can be turned into a ultrametic place. Under this correspondence, (equivalence classes) of ultrametric places of F correspond to prime ideals of OF. For F = Q, this gives back Ostrowski's theorem: any prime ideal in Z (which is necessarily by a single prime number) corresponds to an non-archimedean place and vice versa. However, for more general number fields, the situation becomes more involved, as will be explained below.
Yet another, equivalent way of describing ultrametric places is by means of localizations
Localization of a ring
In abstract algebra, localization is a systematic method of adding multiplicative inverses to a ring. Given a ring R and a subset S, one wants to construct some ring R* and ring homomorphism from R to R*, such that the image of S consists of units in R*...
of OF. Given an ultrametric place v on a number field F, the corresponding localization is the subring T of F of all elements x such that | x |v ≤ 1. By the ultrametric property T is a ring. Moreover, it contains OF. For every element x of F, at least one of x or x−1 is contained in T. Actually, since F×/T× can be shown to be isomorphic to the integers, T is a discrete valuation ring
Discrete valuation ring
In abstract algebra, a discrete valuation ring is a principal ideal domain with exactly one non-zero maximal ideal.This means a DVR is an integral domain R which satisfies any one of the following equivalent conditions:...
, in particular a local ring
Local ring
In abstract algebra, more particularly in ring theory, local rings are certain rings that are comparatively simple, and serve to describe what is called "local behaviour", in the sense of functions defined on varieties or manifolds, or of algebraic number fields examined at a particular place, or...
. Actually, T is just the localization of OF at the prime ideal P. Conversely, P is the maximal ideal of T.
Altogether, there is a three-way equivalence between ultrametric absolute values, prime ideals, and localizations on a number field.
Ramification

Ramification
In mathematics, ramification is a geometric term used for 'branching out', in the way that the square root function, for complex numbers, can be seen to have two branches differing in sign...
, generally speaking, describes a geometric phenomenon that can occur with finite-to-one maps (that is, maps f: X → Y such that the preimages of all points y in Y consist only of finitely many points): the cardinality of the fibers f−1(y) will generally have the same number of points, but it occurs that, in special points y, this number drops. For example, the map
- C → C, z ↦ zn
has n points in each fiber over t, namely the n (complex) roots of t, except in t = 0, where the fiber consists of only one element, z = 0. One says that the map is "ramified" in zero. This is an example of a branched covering
Branched covering
In mathematics, branched covering is a term mainly used in algebraic geometry, to describe morphisms f from an algebraic variety V to another one W, the two dimensions being the same, and the typical fibre of f being of dimension 0....
of Riemann surface
Riemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
s. This intuition also serves to define ramification in algebraic number theory
Splitting of prime ideals in Galois extensions
In mathematics, the interplay between the Galois group G of a Galois extension L of a number field K, and the way the prime ideals P of the ring of integers OK factorise as products of prime ideals of OL, provides one of the richest parts of algebraic number theory...
. Given a (necessarily finite) extension of number fields F / E, a prime ideal p of OE generates the ideal pOF of OF. This ideal may or may not be a prime ideal, but, according to the Lasker–Noether theorem (see above), always is given by
- pOF = q1e1 q2e2 ... qmem
with uniquely determined prime ideals qi of OF and numbers (called ramification indices) ei. Whenever one ramification index is bigger than one, the prime p is said to ramify in F.
The connection between this definition and the geometric situation is delivered by the map of spectra
Spectrum of a ring
In abstract algebra and algebraic geometry, the spectrum of a commutative ring R, denoted by Spec, is the set of all proper prime ideals of R...
of rings Spec OF → Spec OE. In fact, unramified morphisms of scheme
Scheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
s in algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
are a direct generalization of unramified extensions of number fields.
Ramification is a purely local property, i.e., depends only on the completions around the primes p and qi. The inertia group measures the difference between the local Galois groups at some place and the Galois groups of the involved finite residue fields.
An example
The following example illustrates the notions introduced above. In order to compute the ramification index of Q(x), where- f(x) = x3 − x − 1 = 0,
at 23, it suffices to consider the field extension Q23(x) / Q23. Up to 529 = 232 (i.e., modulo
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
529) f can be factored as
- f(x) = (x + 181)(x2 − 181x − 38) = gh.
Substituting x = y + 10 in the first factor g modulo 529 yields y + 191, so the valuation | y |g for y given by g is | −191 |23 = 1. On the other hand the same substitution in h yields Since 161 = 7 × 23,
- |y|h = √ = 1 / √.
Since possible values for the absolute value of the place defined by the factor h are not confined to integer powers of 23, but instead are integer powers of the square root of 23, the ramification index of the field extension at 23 is two.
The valuations of any element of F can be computed in this way using resultants. If, for example y = x2 − x − 1, using the resultant to eliminate x between this relationship and f = x3 − x − 1 = 0 gives . If instead we eliminate with respect to the factors g and h of f, we obtain the corresponding factors for the polynomial for y, and then the 23-adic valuation applied to the constant (norm) term allows us to compute the valuations of y for g and h (which are both 1 in this instance.)
Dedekind discriminant theorem
Much of the significance of the discriminant lies in the fact that ramified ultrametric places are all places obtained from factorizations in Qp where p divides the discriminant. This is even true of the polynomial discriminant; however the converse is also true, that if a prime p divides the discriminant, then there is a p-place which ramifies. For this converse the field discriminant is needed. This is the Dedekind discriminant theorem. In the example above, the discriminant of the number field Q(x) with x3 − x − 1 = 0 is −23, and as we have seen the 23-adic place ramifies. The Dedekind discriminant tells us it is the only ultrametric place which does. The other ramified place comes from the absolute value on the complex embedding of F.Galois groups and Galois cohomology
Generally in abstract algebra, field extensions F / E can be studied by examining the Galois groupGalois group
In mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
Gal(F / E), consisting of field automorphisms of F leaving E elementwise fixed. As an example, the Galois group Gal (Q(ζn) / Q) of the cyclotomic field extension of degree n (see above) is given by (Z/nZ)×, the group of invertible elements in Z/nZ. This is the first stepstone into Iwasawa theory
Iwasawa theory
In number theory, Iwasawa theory is the study of objects of arithmetic interest over infinite towers of number fields. It began as a Galois module theory of ideal class groups, initiated by Kenkichi Iwasawa, in the 1950s, as part of the theory of cyclotomic fields. In the early 1970s, Barry Mazur...
.
In order to include all possible extensions having certain properties, the Galois group concept is commonly applied to the (infinite) field extension / F of the algebraic closure
Algebraic closure
In mathematics, particularly abstract algebra, an algebraic closure of a field K is an algebraic extension of K that is algebraically closed. It is one of many closures in mathematics....
, leading to the absolute Galois group
Absolute Galois group
In mathematics, the absolute Galois group GK of a field K is the Galois group of Ksep over K, where Ksep is a separable closure of K. Alternatively it is the group of all automorphisms of the algebraic closure of K that fix K. The absolute Galois group is unique up to isomorphism...
G := Gal( / F) or just Gal(F), and to the extension F / Q. The fundamental theorem of Galois theory
Fundamental theorem of Galois theory
In mathematics, the fundamental theorem of Galois theory is a result that describes the structure of certain types of field extensions.In its most basic form, the theorem asserts that given a field extension E /F which is finite and Galois, there is a one-to-one correspondence between its...
links fields in between F and its algebraic closure and closed subgroups of Gal (F). For example, the abelianization (the biggest abelian quotient) Gab of G corresponds to a field referred to as the maximal abelian extension
Abelian extension
In abstract algebra, an abelian extension is a Galois extension whose Galois group is abelian. When the Galois group is a cyclic group, we have a cyclic extension. More generally, a Galois extension is called solvable if its Galois group is solvable....
Fab (called so since any further extension is not abelian, i.e., does not have an abelian Galois group). By the Kronecker–Weber theorem
Kronecker–Weber theorem
In algebraic number theory, the Kronecker–Weber theorem states that every finite abelian extension of the field of rational numbers Q, or in other words, every algebraic number field whose Galois group over Q is abelian, is a subfield of a cyclotomic field, i.e. a field obtained by adjoining a root...
, the maximal abelian extension of Q is the extension generated by all roots of unity. For more general number fields, class field theory
Class field theory
In mathematics, class field theory is a major branch of algebraic number theory that studies abelian extensions of number fields.Most of the central results in this area were proved in the period between 1900 and 1950...
, specifically the Artin reciprocity law gives an answer by describing Gab in terms of the idele class group. Also notable is the Hilbert class field
Hilbert class field
In algebraic number theory, the Hilbert class field E of a number field K is the maximal abelian unramified extension of K. Its degree over K equals the class number of K and the Galois group of E over K is canonically isomorphic to the ideal class group of K using Frobenius elements for prime...
, the maximal abelian unramified field extension of F. It can be shown to be finite over F, its Galois group over F is isomorphic to the class group of F, in particular its degree equals the class number h of F (see above).
In certain situations, the Galois group acts
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
on other mathematical objects, for example a group. Such a group is then also referred to as a Galois module. This enables the use of group cohomology
Group cohomology
In abstract algebra, homological algebra, algebraic topology and algebraic number theory, as well as in applications to group theory proper, group cohomology is a way to study groups using a sequence of functors H n. The study of fixed points of groups acting on modules and quotient modules...
for the Galois group Gal(F), also known as Galois cohomology
Galois cohomology
In mathematics, Galois cohomology is the study of the group cohomology of Galois modules, that is, the application of homological algebra to modules for Galois groups...
, which in the first place measures the failure of exactness of taking Gal(F)-invariants, but offers deeper insights (and questions) as well. For example, the Galois group G of a field extension L / F acts on L×, the nonzero elements of L. This Galois module plays a significant role in many arithmetic dualities
Duality (mathematics)
In mathematics, a duality, generally speaking, translates concepts, theorems or mathematical structures into other concepts, theorems or structures, in a one-to-one fashion, often by means of an involution operation: if the dual of A is B, then the dual of B is A. As involutions sometimes have...
, such as Poitou-Tate duality. The Brauer group
Brauer group
In mathematics, the Brauer group of a field K is an abelian group whose elements are Morita equivalence classes of central simple algebras of finite rank over K and addition is induced by the tensor product of algebras. It arose out of attempts to classify division algebras over a field and is...
of F, originally conceived to classify division algebra
Division algebra
In the field of mathematics called abstract algebra, a division algebra is, roughly speaking, an algebra over a field, in which division is possible.- Definitions :...
s over F, can be recast as a cohomology group, namely H2(Gal (F), ×).
Local-global principle
Generally speaking, the term "local to global" refers to the idea that a global problem is first done at a local level, which tends to simplify the questions. Then, of course, the information gained in the local analysis has to be put together to get back to some global statement. For example, the notion of sheavesSheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
reifies that idea in topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
and geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
.
Local and global fields
Number fields share a great deal of similarity with another class of fields much used in algebraic geometryAlgebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
known as function fields
Function field of an algebraic variety
In algebraic geometry, the function field of an algebraic variety V consists of objects which are interpreted as rational functions on V...
of algebraic curve
Algebraic curve
In algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...
s over finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
s. An example is Fp(T). They are similar in many respects, for example in that number rings are one-dimensional regular rings, as are the coordinate rings (the quotient fields of which is the function field in question) of curves. Therefore, both types of field are called global field
Global field
In mathematics, the term global field refers to either of the following:*an algebraic number field, i.e., a finite extension of Q, or*a global function field, i.e., the function field of an algebraic curve over a finite field, equivalently, a finite extension of Fq, the field of rational functions...
s. In accordance with the philosophy laid out above, they can be studied at a local level first, that is to say, by looking at the corresponding local field
Local field
In mathematics, a local field is a special type of field that is a locally compact topological field with respect to a non-discrete topology.Given such a field, an absolute value can be defined on it. There are two basic types of local field: those in which the absolute value is archimedean and...
s. For number fields F, the local fields are the completions of F at all places, including the archimedean ones (see local analysis
Local analysis
In mathematics, the term local analysis has at least two meanings - both derived from the idea of looking at a problem relative to each prime number p first, and then later trying to integrate the information gained at each prime into a 'global' picture...
). For function fields, the local fields are completions of the local rings at all points of the curve for function fields.
Many results valid for function fields also hold, at least if reformulated properly, for number fields. However, the study of number fields often poses difficulties and phenomena not encountered in function fields. For example, in function fields, there is no dichotomy into non-archimedean and archimedean places. Nonetheless, function fields often serves as a source of intuition what should be expected in the number field case.
The Hasse principle
A prototypical question, posed at a global level, is whether some polynomial equation has a solution in F. If this is the case, this solution is also a solution in all completions. The local-global principle or Hasse principle asserts that for quadratic equations, the converse holds, as well. Thereby, checking whether such an equation has a solution can be done on all the completions of F, which is often easier, since analytic methods (classical analytic tools such as intermediate value theoremIntermediate value theorem
In mathematical analysis, the intermediate value theorem states that for each value between the least upper bound and greatest lower bound of the image of a continuous function there is at least one point in its domain that the function maps to that value....
at the archimedean places and p-adic analysis
P-adic analysis
In mathematics, p-adic analysis is a branch of number theory that deals with the mathematical analysis of functions of p-adic numbers....
at the nonarchimedean places) can be used. This implication does not hold, however, for more general types of equations. However, the idea of passing from local data to global ones proves fruitful in class field theory, for example, where local class field theory is used to obtain global insights mentioned above. This is also related to the fact that the Galois groups of the completions Fv can be explicitly determined, whereas the Galois groups of global fields, even of Q are far less understood.
Adeles and ideles
In order to assemble local data pertaining to all local fields attached to F, the adele ringAdele ring
In algebraic number theory and topological algebra, the adele ring is a topological ring which is built on the field of rational numbers . It involves all the completions of the field....
is set up. A multiplicative variant is referred to as ideles.
See also
- Dirichlet's unit theoremDirichlet's unit theoremIn mathematics, Dirichlet's unit theorem is a basic result in algebraic number theory due to Gustav Lejeune Dirichlet. It determines the rank of the group of units in the ring OK of algebraic integers of a number field K...
, S-unitS-unitIn mathematics, in the field of algebraic number theory, an S-unit generalises the idea of unit of the ring of integers of the field. Many of the results which hold for units are also valid for S-units.-Definition:... - Kummer extension
- Minkowski's theoremMinkowski's theoremIn mathematics, Minkowski's theorem is the statement that any convex set in Rn which is symmetric with respect to the origin and with volume greater than 2n d contains a non-zero lattice point...
, Geometry of numbersGeometry of numbersIn number theory, the geometry of numbers studies convex bodies and integer vectors in n-dimensional space. The geometry of numbers was initiated by .... - Chebotarev's density theoremChebotarev's density theoremChebotarev's density theorem in algebraic number theory describes statistically the splitting of primes in a given Galois extension K of the field Q of rational numbers. Generally speaking, a prime integer will factor into several ideal primes in the ring of algebraic integers of K. There are only...
- Ray class group
- Decomposition group
- Genus fieldGenus fieldIn algebraic number theory, the genus field G of a number field K is the maximal abelian extension of K which is obtained by composing an absolutely abelian field with K and which is unramified at all finite primes of K...