Integrally closed domain
Encyclopedia
In commutative algebra
, an integrally closed domain A is an integral domain whose integral closure in the field of fractions of A is A itself. Many well-studied domains are integrally closed: Field
s, the ring of integers Z, unique factorization domain
s and regular local rings are all integrally closed.
To give a non-example, let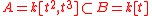
(k a field). A and B have the same field of fractions, and B is the integral closure of A (since B is a UFD.) In other words, A is not integrally closed. This is related to the fact that the plane curve 
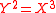has a singularity at the origin.
Let A be an integrally closed domain with field of fractions K and a finite extension L of K. Then x in L is integral over A if and only if its minimal polynomial over K has coefficients in A. This implies in particular that an integral element over an integrally closed domain has a minimal polynomial over A: this is stronger than that an integral element satisfying some monic polynomial. In fact, the statement is false without "integrally closed" (consider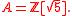
)
Integrally closed domains also play a role in the hypothesis of the Going-down theorem. The theorem states that if A⊆B is an integral extension of domains and A is an integrally closed domain, then the going-down property
holds for the extension A⊆B.
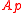over prime ideals 
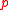of height 1.
For a noetherian local domain A of dimension one, the following are equivalent.
, Grothendieck
, and Matsumura define a normal ring to be a ring whose localizations at prime ideals are integrally closed domains. Such a ring is necessarily a reduced ring
, and this is sometimes included in the definition. In general, if A is a Noetherian
ring whose localizations at maximal ideals are all domains, then A is a finite product of domains. In particular if A is a Noetherian, normal ring, then the domains in the product are integrally closed domains. Conversely, any finite product of integrally closed domains is normal.
Let A be a noetherian ring. Then A is normal if and only if it satisfies the following: for any prime ideal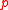
,
Item (i) is often phrased as "regular in codimension 1". Note (i) implies that the set of associated primes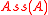
has no embedded primes, and, when (i) is the case, (ii) means that 
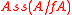has no embedded prime for any nonzero zero-divisor f. In particular, a Cohen-Macaulay ring
satisfies (ii). Geometrically, we have the following: if X is a local complete intersection in a nonsingular variety; e.g., X itself is nonsingular, then X is Cohen-Macaulay; i.e., the stalks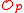
of the structure sheaf are Cohen-Macaulay for all prime ideals p. Then we can say: X is normal
(i.e., the stalks of its structure sheaf are all normal) if and only if it is regular in codimension 1.
Let A be a domain and K its field of fractions. x in K is said to be almost integral over A if there is a
such that 
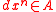for all 
. Then A is said to be completely integrally closed if every almost integral element of K is contained in A. A completely integrally closed domain is integrally closed. Conversely, a noetherian integrally closed domain is completely integrally closed.
Assume A is completely integrally closed. Then the formal power series ring
is completely integrally closed. This is significant since the analog is false for an integrally closed domain: let R be a valuation domain of height at least 2 (which is integrally closed.) Then 
is not integrally closed. Let L be a field extension of K. Then the integral closure of A in L is completely integrally closed.
1 → 2 results immediately from the preservation of integral closure under localization; 2 → 3 is trivial; 3 → 1 results from the preservation of integral closure under localization, the exactness of localization, and the property that an A-module M is zero if and only if its localization with respect to every maximal ideal is zero.
In contrast, the "integrally closed" does not pass over quotient, for Z[t]/(t2+4) is not integrally closed.
The localization of a completely integrally closed need not be completely integrally closed.
Commutative algebra
Commutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
, an integrally closed domain A is an integral domain whose integral closure in the field of fractions of A is A itself. Many well-studied domains are integrally closed: Field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
s, the ring of integers Z, unique factorization domain
Unique factorization domain
In mathematics, a unique factorization domain is, roughly speaking, a commutative ring in which every element, with special exceptions, can be uniquely written as a product of prime elements , analogous to the fundamental theorem of arithmetic for the integers...
s and regular local rings are all integrally closed.
To give a non-example, let
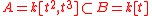(k a field). A and B have the same field of fractions, and B is the integral closure of A (since B is a UFD.) In other words, A is not integrally closed. This is related to the fact that the plane curve 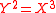has a singularity at the origin.Let A be an integrally closed domain with field of fractions K and a finite extension L of K. Then x in L is integral over A if and only if its minimal polynomial over K has coefficients in A. This implies in particular that an integral element over an integrally closed domain has a minimal polynomial over A: this is stronger than that an integral element satisfying some monic polynomial. In fact, the statement is false without "integrally closed" (consider
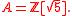)Integrally closed domains also play a role in the hypothesis of the Going-down theorem. The theorem states that if A⊆B is an integral extension of domains and A is an integrally closed domain, then the going-down property
Going up and going down
In commutative algebra, a branch of mathematics, going up and going down are terms which refer to certain properties of chains of prime ideals in integral extensions....
holds for the extension A⊆B.
Examples
The following are integrally closed domains.- Any principal ideal domain (in particular, any field).
- Any unique factorization domainUnique factorization domainIn mathematics, a unique factorization domain is, roughly speaking, a commutative ring in which every element, with special exceptions, can be uniquely written as a product of prime elements , analogous to the fundamental theorem of arithmetic for the integers...
(in particular, any polynomial ring over a unique factorization domain.) - Any GCD domainGCD domainIn mathematics, a GCD domain is an integral domain R with the property that any two non-zero elements have a greatest common divisor . Equivalently, any two non-zero elements of R have a least common multiple ....
(in particular, any Bezout domainBézout domainIn mathematics, a Bézout domain is an integral domain in which the sum of two principal ideals is again a principal ideal. This means that for every pair of elements a Bézout identity holds, and that every finitely generated ideal is principal...
or valuation domain). - Any Dedekind domainDedekind domainIn abstract algebra, a Dedekind domain or Dedekind ring, named after Richard Dedekind, is an integral domain in which every nonzero proper ideal factors into a product of prime ideals. It can be shown that such a factorization is then necessarily unique up to the order of the factors...
- Any symmetric algebraSymmetric algebraIn mathematics, the symmetric algebra S on a vector space V over a field K is the free commutative unital associative algebra over K containing V....
over a field (since every symmetric algebra is isomorphic to a polynomial ring in several variables over a field)
Noetherian integrally closed domain
If A is a noetherian integrally closed domain, then A is the intersection of all localizations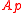 over prime ideals 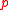of height 1.For a noetherian local domain A of dimension one, the following are equivalent.
- A is integrally closed.
- The maximal ideal of A is principal.
- A is a discrete valuation ringDiscrete valuation ringIn abstract algebra, a discrete valuation ring is a principal ideal domain with exactly one non-zero maximal ideal.This means a DVR is an integral domain R which satisfies any one of the following equivalent conditions:...
(equivalently A is Dedekind.) - A is a regular local ring.
Related notions
Authors including SerreJean-Pierre Serre
Jean-Pierre Serre is a French mathematician. He has made contributions in the fields of algebraic geometry, number theory, and topology.-Early years:...
, Grothendieck
Alexander Grothendieck
Alexander Grothendieck is a mathematician and the central figure behind the creation of the modern theory of algebraic geometry. His research program vastly extended the scope of the field, incorporating major elements of commutative algebra, homological algebra, sheaf theory, and category theory...
, and Matsumura define a normal ring to be a ring whose localizations at prime ideals are integrally closed domains. Such a ring is necessarily a reduced ring
Reduced ring
In ring theory, a ring R is called a reduced ring if it has no non-zero nilpotent elements. Equivalently, a ring is reduced if it has no non-zero elements with square zero, that is, x2 = 0 implies x = 0...
, and this is sometimes included in the definition. In general, if A is a Noetherian
Noetherian ring
In mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element...
ring whose localizations at maximal ideals are all domains, then A is a finite product of domains. In particular if A is a Noetherian, normal ring, then the domains in the product are integrally closed domains. Conversely, any finite product of integrally closed domains is normal.
Let A be a noetherian ring. Then A is normal if and only if it satisfies the following: for any prime ideal
,
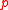- (i) If
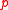has height 
, then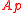 
is regularRegular local ringIn commutative algebra, a regular local ring is a Noetherian local ring having the property that the minimal number of generators of its maximal ideal is equal to its Krull dimension. In symbols, let A be a Noetherian local ring with maximal ideal m, and suppose a1, ..., an is a minimal set of...
(i.e.,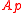
is a discrete valuation ringDiscrete valuation ringIn abstract algebra, a discrete valuation ring is a principal ideal domain with exactly one non-zero maximal ideal.This means a DVR is an integral domain R which satisfies any one of the following equivalent conditions:...
.) - (ii) If
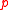has height 
, then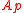 
has depth 
.
Item (i) is often phrased as "regular in codimension 1". Note (i) implies that the set of associated primes
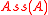has no embedded primes, and, when (i) is the case, (ii) means that 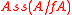has no embedded prime for any nonzero zero-divisor f. In particular, a Cohen-Macaulay ringCohen-Macaulay ring
In mathematics, a Cohen–Macaulay ring is a particular type of commutative ring, possessing some of the algebraic-geometric properties of a nonsingular variety, such as local equidimensionality....
satisfies (ii). Geometrically, we have the following: if X is a local complete intersection in a nonsingular variety; e.g., X itself is nonsingular, then X is Cohen-Macaulay; i.e., the stalks
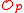of the structure sheaf are Cohen-Macaulay for all prime ideals p. Then we can say: X is normalNormal scheme
In mathematics, in the field of algebraic geometry, a normal scheme is a scheme X for which every stalk of its structure sheaf OX is an integrally closed local ring; that is, each stalk is an integral domain such that its integral closure in its field of fractions is equal to itself.Any reduced...
(i.e., the stalks of its structure sheaf are all normal) if and only if it is regular in codimension 1.
Let A be a domain and K its field of fractions. x in K is said to be almost integral over A if there is a
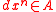such that for all . Then A is said to be completely integrally closed if every almost integral element of K is contained in A. A completely integrally closed domain is integrally closed. Conversely, a noetherian integrally closed domain is completely integrally closed.Assume A is completely integrally closed. Then the formal power series ring
is completely integrally closed. This is significant since the analog is false for an integrally closed domain: let R be a valuation domain of height at least 2 (which is integrally closed.) Then is not integrally closed. Let L be a field extension of K. Then the integral closure of A in L is completely integrally closed."Integrally closed" under constructions
The following conditions are equivalent for an integral domain A:- A is integrally closed;
- Ap (the localization of A with respect to p) is integrally closed for every prime idealPrime idealIn algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...
p; - Am is integrally closed for every maximal idealMaximal idealIn mathematics, more specifically in ring theory, a maximal ideal is an ideal which is maximal amongst all proper ideals. In other words, I is a maximal ideal of a ring R if I is an ideal of R, I ≠ R, and whenever J is another ideal containing I as a subset, then either J = I or J = R...
m.
1 → 2 results immediately from the preservation of integral closure under localization; 2 → 3 is trivial; 3 → 1 results from the preservation of integral closure under localization, the exactness of localization, and the property that an A-module M is zero if and only if its localization with respect to every maximal ideal is zero.
In contrast, the "integrally closed" does not pass over quotient, for Z[t]/(t2+4) is not integrally closed.
The localization of a completely integrally closed need not be completely integrally closed.