
Subgroup
Encyclopedia
In group theory
, given a group
G under a binary operation
*, a subset
H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H. This is usually represented notationally by H ≤ G, read as "H is a subgroup of G".
A proper subgroup of a group G is a subgroup H which is a proper subset
of G (i.e. H ≠ G). The trivial subgroup of any group is the subgroup {e} consisting of just the identity element. If H is a subgroup of G, then G is sometimes called an overgroup of H.
The same definitions apply more generally when G is an arbitrary semigroup
, but this article will only deal with subgroups of groups. The group G is sometimes denoted by the ordered pair (G,*), usually to emphasize the operation * when G carries multiple algebraic or other structures.
This article will write ab for a*b, as is usual.
aH = {ah : h in H}. Because a is invertible, the map φ : H → aH given by φ(h) = ah is a bijection
. Furthermore, every element of G is contained in precisely one left coset of H; the left cosets are the equivalence classes corresponding to the equivalence relation
a1 ~ a2 if and only if
a1−1a2 is in H. The number of left cosets of H is called the index
of H in G and is denoted by [G : H].
Lagrange's theorem
states that for a finite group G and a subgroup H,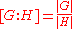
where |G| and |H| denote the order
s of G and H, respectively. In particular, the order of every subgroup of G (and the order of every element of G) must be a divisor
of |G|.
Right cosets are defined analogously: Ha = {ha : h in H}. They are also the equivalence classes for a suitable equivalence relation and their number is equal to [G : H].
If aH = Ha for every a in G, then H is said to be a normal subgroup
. Every subgroup of index 2 is normal: the left cosets, and also the right cosets, are simply the subgroup and its complement. More generally, if p is the lowest prime dividing the order of a finite group G, then any subgroup of index p (if such exists) is normal.
Z8 whose elements are
and whose group operation is addition modulo eight
. Its Cayley table
is
This group has a pair of nontrivial subgroups: J={0,4} and H={0,2,4,6}, where J is also a subgroup of H. The Cayley table for H is the top-left quadrant of the Cayley table for G. The group G is cyclic
, and so are its subgroups. In general, subgroups of cyclic groups are also cyclic.
The trivial group
and two-element groups Z2. These small subgroups are not counted in the following list.
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, given a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
G under a binary operation
Binary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
*, a subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H. This is usually represented notationally by H ≤ G, read as "H is a subgroup of G".
A proper subgroup of a group G is a subgroup H which is a proper subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of G (i.e. H ≠ G). The trivial subgroup of any group is the subgroup {e} consisting of just the identity element. If H is a subgroup of G, then G is sometimes called an overgroup of H.
The same definitions apply more generally when G is an arbitrary semigroup
Semigroup
In mathematics, a semigroup is an algebraic structure consisting of a set together with an associative binary operation. A semigroup generalizes a monoid in that there might not exist an identity element...
, but this article will only deal with subgroups of groups. The group G is sometimes denoted by the ordered pair (G,*), usually to emphasize the operation * when G carries multiple algebraic or other structures.
This article will write ab for a*b, as is usual.
Basic properties of subgroups
- A subset H of the group G is a subgroup of G if and only if it is nonempty and closed under products and inverses. (The closure conditions mean the following: whenever a and b are in H, then ab and a−1 are also in H. These two conditions can be combined into one equivalent condition: whenever a and b are in H, then ab−1 is also in H.) In the case that H is finite, then H is a subgroup if and only ifIf and only ifIn logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
H is closed under products. (In this case, every element a of H generates a finite cyclic subgroup of H, and the inverse of a is then a−1 = an − 1, where n is the order of a.) - The above condition can be stated in terms of a homomorphismHomomorphismIn abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
; that is, H is a subgroup of a group G if and only if H is a subset of G and there is an inclusion homomorphism (i.e., i(a) = a for every a) from H to G. - The identityIdentity elementIn mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
of a subgroup is the identity of the group: if G is a group with identity eG, and H is a subgroup of G with identity eH, then eH = eG. - The inverseInverse elementIn abstract algebra, the idea of an inverse element generalises the concept of a negation, in relation to addition, and a reciprocal, in relation to multiplication. The intuition is of an element that can 'undo' the effect of combination with another given element...
of an element in a subgroup is the inverse of the element in the group: if H is a subgroup of a group G, and a and b are elements of H such that ab = ba = eH, then ab = ba = eG. - The intersectionIntersection (set theory)In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
of subgroups A and B is again a subgroup. The unionUnion (set theory)In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
of subgroups A and B is a subgroup if and only if either A or B contains the other, since for example 2 and 3 are in the union of 2Z and 3Z but their sum 5 is not. Another example is the union of the x-axis and the y-axis in the plane (with the addition operation); each of these objects is a subgroup but their union is not. This also serves as an example of two subgroups, whose intersection is precisely the identity. - If S is a subset of G, then there exists a minimum subgroup containing S, which can be found by taking the intersection of all of subgroups containing S; it is denoted by
and is said to be the subgroup generated by SGenerating set of a groupIn abstract algebra, a generating set of a group is a subset that is not contained in any proper subgroup of the group. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination of finitely many elements of the subset and their...
. An element of G is inif and only if it is a finite product of elements of S and their inverses. - Every element a of a group G generates the cyclic subgroup . If is isomorphicGroup isomorphismIn abstract algebra, a group isomorphism is a function between two groups that sets up a one-to-one correspondence between the elements of the groups in a way that respects the given group operations. If there exists an isomorphism between two groups, then the groups are called isomorphic...
to Z/nZ for some positive integer n, then n is the smallest positive integer for which an = e, and n is called the order of a. If is isomorphic to Z, then a is said to have infinite order. - The subgroups of any given group form a complete latticeComplete latticeIn mathematics, a complete lattice is a partially ordered set in which all subsets have both a supremum and an infimum . Complete lattices appear in many applications in mathematics and computer science...
under inclusion, called the lattice of subgroupsLattice of subgroupsIn mathematics, the lattice of subgroups of a group G is the lattice whose elements are the subgroups of G, with the partial order relation being set inclusion....
. (While the infimumInfimumIn mathematics, the infimum of a subset S of some partially ordered set T is the greatest element of T that is less than or equal to all elements of S. Consequently the term greatest lower bound is also commonly used...
here is the usual set-theoretic intersection, the supremumSupremumIn mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...
of a set of subgroups is the subgroup generated by the set-theoretic union of the subgroups, not the set-theoretic union itself.) If e is the identity of G, then the trivial group {e} is the minimum subgroup of G, while the maximum subgroup is the group G itself.
Cosets and Lagrange's theorem
Given a subgroup H and some a in G, we define the left cosetCoset
In mathematics, if G is a group, and H is a subgroup of G, and g is an element of G, thenA coset is a left or right coset of some subgroup in G...
aH = {ah : h in H}. Because a is invertible, the map φ : H → aH given by φ(h) = ah is a bijection
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
. Furthermore, every element of G is contained in precisely one left coset of H; the left cosets are the equivalence classes corresponding to the equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
a1 ~ a2 if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
a1−1a2 is in H. The number of left cosets of H is called the index
Index of a subgroup
In mathematics, specifically group theory, the index of a subgroup H in a group G is the "relative size" of H in G: equivalently, the number of "copies" of H that fill up G. For example, if H has index 2 in G, then intuitively "half" of the elements of G lie in H...
of H in G and is denoted by [G : H].
Lagrange's theorem
Lagrange's theorem (group theory)
Lagrange's theorem, in the mathematics of group theory, states that for any finite group G, the order of every subgroup H of G divides the order of G. The theorem is named after Joseph Lagrange....
states that for a finite group G and a subgroup H,
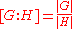
where |G| and |H| denote the order
Order (group theory)
In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
s of G and H, respectively. In particular, the order of every subgroup of G (and the order of every element of G) must be a divisor
Divisor
In mathematics, a divisor of an integer n, also called a factor of n, is an integer which divides n without leaving a remainder.-Explanation:...
of |G|.
Right cosets are defined analogously: Ha = {ha : h in H}. They are also the equivalence classes for a suitable equivalence relation and their number is equal to [G : H].
If aH = Ha for every a in G, then H is said to be a normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
. Every subgroup of index 2 is normal: the left cosets, and also the right cosets, are simply the subgroup and its complement. More generally, if p is the lowest prime dividing the order of a finite group G, then any subgroup of index p (if such exists) is normal.
Example: Subgroups of Z8
Let G be the cyclic groupCyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
Z8 whose elements are

and whose group operation is addition modulo eight
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
. Its Cayley table
Cayley table
A Cayley table, after the 19th century British mathematician Arthur Cayley, describes the structure of a finite group by arranging all the possible products of all the group's elements in a square table reminiscent of an addition or multiplication table...
is
| + | 0 | 2 | 4 | 6 | 1 | 3 | 5 | 7 |
|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 2 | 4 | 6 | 1 | 3 | 5 | 7 |
| 2 | 2 | 4 | 6 | 0 | 3 | 5 | 7 | 1 |
| 4 | 4 | 6 | 0 | 2 | 5 | 7 | 1 | 3 |
| 6 | 6 | 0 | 2 | 4 | 7 | 1 | 3 | 5 |
| 1 | 1 | 3 | 5 | 7 | 2 | 4 | 6 | 0 |
| 3 | 3 | 5 | 7 | 1 | 4 | 6 | 0 | 2 |
| 5 | 5 | 7 | 1 | 3 | 6 | 0 | 2 | 4 |
| 7 | 7 | 1 | 3 | 5 | 0 | 2 | 4 | 6 |
This group has a pair of nontrivial subgroups: J={0,4} and H={0,2,4,6}, where J is also a subgroup of H. The Cayley table for H is the top-left quadrant of the Cayley table for G. The group G is cyclic
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
, and so are its subgroups. In general, subgroups of cyclic groups are also cyclic.
Example: Subgroups of S4
Every group has as many small subgroups as neutral elements on the main diagonal:The trivial group
Trivial group
In mathematics, a trivial group is a group consisting of a single element. All such groups are isomorphic so one often speaks of the trivial group. The single element of the trivial group is the identity element so it usually denoted as such, 0, 1 or e depending on the context...
and two-element groups Z2. These small subgroups are not counted in the following list.

