Multiplicative group
Encyclopedia
In mathematics
and group theory
the term multiplicative group refers to one of the following concepts, depending on the context
-th roots of unity is by definition the kernel of the 
-power map on the multiplicative group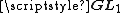 
, considered as a group scheme
. That is, for any integer
we can consider the morphism on the multiplicative group that takes 
-th powers, and take an appropriate fiber product in the sense of scheme theory of it, with the morphism 
that serves as the identity.
The resulting group scheme is written
. It gives rise to a reduced scheme, when we take it over a field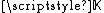 
, if and only if
the characteristic of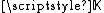
does not divide 
. This makes it a source of some key examples of non-reduced schemes (schemes with nilpotent elements in their structure sheaves); for example 
over a finite field
with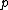
elements for any prime number
.
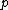This phenomenon is not easily expressed in the classical language of algebraic geometry. It turns out to be of major importance, for example, in expressing the duality theory of abelian varieties in characteristic
(theory of Pierre Cartier
). The Galois cohomology of this group scheme is a way of expressing Kummer theory
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
the term multiplicative group refers to one of the following concepts, depending on the context
- any group
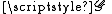whose binary operationBinary operationIn mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
is written in multiplicative notation (instead of being written in additive notation as usual for abelian groupAbelian groupIn abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s), - the underlying group under multiplication of the invertible elements of a fieldField (mathematics)In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
, ringRing (mathematics)In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
, or other structure having multiplication as one of its operations. In the case of a field F, the group is {F - {0}, •}, where 0 refers to the zero elementZero elementIn mathematics, a zero element is one of several generalizations of the number zero to other algebraic structures. These alternate meanings may or may not reduce to the same thing, depending on the context.-Additive identities:...
of the F and the binary operationBinary operationIn mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
• is the field multiplicationMultiplicationMultiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
, - the algebraic torusAlgebraic torusIn mathematics, an algebraic torus is a type of commutative affine algebraic group. These groups were named by analogy with the theory of tori in Lie group theory...
.
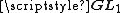Group scheme of roots of unity
The group scheme of-th roots of unity is by definition the kernel of the -power map on the multiplicative group 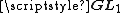, considered as a group schemeGroup scheme
In mathematics, a group scheme is a type of algebro-geometric object equipped with a composition law. Group schemes arise naturally as symmetries of schemes, and they generalize algebraic groups, in the sense that all algebraic groups have group scheme structure, but group schemes are not...
. That is, for any integer
we can consider the morphism on the multiplicative group that takes -th powers, and take an appropriate fiber product in the sense of scheme theory of it, with the morphism that serves as the identity.The resulting group scheme is written
. It gives rise to a reduced scheme, when we take it over a field 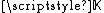, if and only ifIf and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
the characteristic of
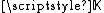does not divide . This makes it a source of some key examples of non-reduced schemes (schemes with nilpotent elements in their structure sheaves); for example 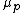over a finite fieldFinite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
with
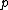elements for any prime numberPrime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
.This phenomenon is not easily expressed in the classical language of algebraic geometry. It turns out to be of major importance, for example, in expressing the duality theory of abelian varieties in characteristic
(theory of Pierre CartierPierre Cartier (mathematician)
Pierre Cartier is a mathematician. An associate of the Bourbaki group and at one time a colleague of Alexander Grothendieck, his interests have ranged over algebraic geometry, representation theory, mathematical physics, and category theory....
). The Galois cohomology of this group scheme is a way of expressing Kummer theory
Kummer theory
In abstract algebra and number theory, Kummer theory provides a description of certain types of field extensions involving the adjunction of nth roots of elements of the base field. The theory was originally developed by Ernst Eduard Kummer around the 1840s in his pioneering work on Fermat's last...
.
See also
- multiplicative group of integers modulo nMultiplicative group of integers modulo nIn modular arithmetic the set of congruence classes relatively prime to the modulus n form a group under multiplication called the multiplicative group of integers modulo n. It is also called the group of primitive residue classes modulo n. In the theory of rings, a branch of abstract algebra, it...
- additive groupAdditive groupAn additive group may refer to:*an abelian group, when it is written using the symbol + for its binary operation*a group scheme representing the underlying-additive-group functor...