In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, the Laurent series of a complex function f(z) is a representation of that function as a power series which includes terms of negative degree. It may be used to express complex functions in cases where
a Taylor series

Taylor series

In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....

 expansion cannot be applied. The Laurent series was named
after and first published by Pierre Alphonse Laurent

Pierre Alphonse Laurent

Pierre Alphonse Laurent was a French mathematician best known as the discoverer of the Laurent series, an expansion of a function into an infinite power series, generalizing the Taylor series expansion. He was born in Paris, France...

 in 1843.
Karl Weierstrass

Karl Weierstrass

Karl Theodor Wilhelm Weierstrass was a German mathematician who is often cited as the "father of modern analysis".- Biography :Weierstrass was born in Ostenfelde, part of Ennigerloh, Province of Westphalia....

 may have discovered it first in 1841 but did not publish it at the time.

The Laurent series for a complex function f(z) about a point c is given by:


where the a_n are constants, defined by a line integral

Line integral

In mathematics, a line integral is an integral where the function to be integrated is evaluated along a curve.The function to be integrated may be a scalar field or a vector field...

which is a generalization of Cauchy's integral formula

Cauchy's integral formula

In mathematics, Cauchy's integral formula, named after Augustin-Louis Cauchy, is a central statement in complex analysis. It expresses the fact that a holomorphic function defined on a disk is completely determined by its values on the boundary of the disk, and it provides integral formulas for all...

:


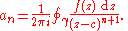
The path of integration γ is counterclockwise around a closed,
rectifiable path containing no self-intersections, enclosing
c and lying in an annulus

Annulus (mathematics)

In mathematics, an annulus is a ring-shaped geometric figure, or more generally, a term used to name a ring-shaped object. Or, it is the area between two concentric circles...

 A in which 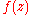is
holomorphic

Holomorphic function

In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...

 (analytic).