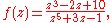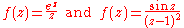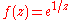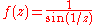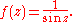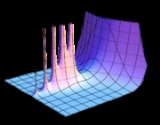
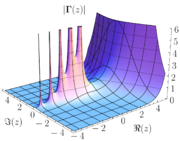
Meromorphic function
Encyclopedia
In complex analysis
, a meromorphic function on an open subset
D of the complex plane
is a function
that is holomorphic
on all D except a set of isolated point
s, which are poles for the function. (The terminology comes from the Ancient Greek
meros (μέρος), meaning part, as opposed to holos (ὅλος), meaning whole.)
Every meromorphic function on D can be expressed as the ratio between two holomorphic function
s (with the denominator not constant 0) defined on D: any pole must coincide with a zero of the denominator.
Intuitively then, a meromorphic function is a ratio of two well-behaved (holomorphic) functions. Such a function will still be well-behaved, except possibly at the points where the denominator of the fraction is zero. (If the denominator has a zero at z and the numerator does not, then the value of the function will be infinite; if both parts have a zero at z, then one must compare the multiplicities
of these zeros.)
From an algebraic point of view, if D is connected, then the set of meromorphic functions is the field of fractions
of the integral domain of the set of holomorphic functions. This is analogous to the relationship between
, the rational number
s, and
, the integer
s.
Additionally, in group theory
of the 1930s, a meromorphic function (or simply a meromorph) was a function from a group G into itself which preserves the product on the group. The image of this function was called an automorphism of G. (Similarly, a homomorphic function (or homomorph) was a function between groups which preserved the product while a homomorphism was the image of a homomorph.) This terminology has been replaced with use of endomorphism for the function itself with no special name given to the image of the function and thus meromorph no longer has an implied
meaning within group theory.
By using analytic continuation
to eliminate removable singularities, meromorphic functions can be added, subtracted, multiplied, and the quotient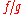
can be formed unless 
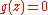on a connected component
of D. Thus, if D is connected, the meromorphic functions form a field
, in fact a field extension
of the complex numbers.
every point admits an open neighborhood
which is homeomorphic
to an open subset of the complex plane. Thereby the notion of a meromorphic function can be defined for every Riemann surface.
When D is the entire Riemann sphere
, the field of meromorphic functions is simply the field of rational functions in one variable over the complex field, since one can prove that any meromorphic function on the sphere is rational. (This is a special case of the so-called GAGA
principle.)
For every Riemann surface
, a meromorphic function is the same as a holomorphic function that maps to the Riemann sphere and which is not constant ∞. The poles correspond to those complex numbers which are mapped to ∞.
On a non-compact Riemann surface
every meromorphic function can be realized as a quotient of two (globally defined) holomorphic functions. In contrast, on a compact Riemann surface every holomorphic function is constant, while there always exist non-constant meromorphic functions.
Meromorphic functions on an elliptic curve
are also known as elliptic function
s.
, a meromorphic function is defined to be locally a quotient of two holomorphic functions. For example,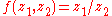
is a meromorphic function on the two-dimensional complex affine space. Here it is no longer true that every meromorphic function can be regarded as holomorphic function with values in the Riemann sphere
: There is a set of "indeterminacy" of codimension
two (in the given example this set consists of the origin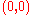
).
Unlike in dimension one, in higher dimensions there do exist complex manifold
s on which there are no non-constant holomorphic functions, for example, most complex tori
.
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
, a meromorphic function on an open subset
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
D of the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
is a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
that is holomorphic
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
on all D except a set of isolated point
Isolated point
In topology, a branch of mathematics, a point x of a set S is called an isolated point of S, if there exists a neighborhood of x not containing other points of S.In particular, in a Euclidean space ,...
s, which are poles for the function. (The terminology comes from the Ancient Greek
Ancient Greek
Ancient Greek is the stage of the Greek language in the periods spanning the times c. 9th–6th centuries BC, , c. 5th–4th centuries BC , and the c. 3rd century BC – 6th century AD of ancient Greece and the ancient world; being predated in the 2nd millennium BC by Mycenaean Greek...
meros (μέρος), meaning part, as opposed to holos (ὅλος), meaning whole.)
Every meromorphic function on D can be expressed as the ratio between two holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
s (with the denominator not constant 0) defined on D: any pole must coincide with a zero of the denominator.
Zero (complex analysis)
In complex analysis, a zero of a holomorphic function f is a complex number a such that f = 0.-Multiplicity of a zero:A complex number a is a simple zero of f, or a zero of multiplicity 1 of f, if f can be written asf=g\,where g is a holomorphic function g such that g is not zero.Generally, the...
of these zeros.)
From an algebraic point of view, if D is connected, then the set of meromorphic functions is the field of fractions
Field of fractions
In abstract algebra, the field of fractions or field of quotients of an integral domain is the smallest field in which it can be embedded. The elements of the field of fractions of the integral domain R have the form a/b with a and b in R and b ≠ 0...
of the integral domain of the set of holomorphic functions. This is analogous to the relationship between
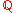, the rational numberRational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s, and
, the integerInteger
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s.
Additionally, in group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
of the 1930s, a meromorphic function (or simply a meromorph) was a function from a group G into itself which preserves the product on the group. The image of this function was called an automorphism of G. (Similarly, a homomorphic function (or homomorph) was a function between groups which preserved the product while a homomorphism was the image of a homomorph.) This terminology has been replaced with use of endomorphism for the function itself with no special name given to the image of the function and thus meromorph no longer has an implied
meaning within group theory.
Examples
- All rational functionRational functionIn mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
s such as
-
- are meromorphic on the whole complex plane.
- The functions
- as well as the gamma functionGamma functionIn mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
and the Riemann zeta function are meromorphic on the whole complex plane.- The function
- is defined in the whole complex plane except for the origin, 0. However, 0 is not a pole of this function, rather an essential singularityEssential singularityIn complex analysis, an essential singularity of a function is a "severe" singularity near which the function exhibits extreme behavior.The category essential singularity is a "left-over" or default group of singularities that are especially unmanageable: by definition they fit into neither of the...
. Thus, this function is not meromorphic in the whole complex plane. However, it is meromorphic (even holomorphic) on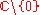
.
- The complex logarithmComplex logarithmIn complex analysis, a complex logarithm function is an "inverse" of the complex exponential function, just as the natural logarithm ln x is the inverse of the real exponential function ex. Thus, a logarithm of z is a complex number w such that ew = z. The notation for such a w is log z...
function
- The complex logarithm
- is not meromorphic on the whole complex plane, as it cannot be defined on the whole complex plane less an isolated set of points.
- The function
- is not meromorphic in the whole plane, since the point
is an accumulation pointLimit pointIn mathematics, a limit point of a set S in a topological space X is a point x in X that can be "approximated" by points of S in the sense that every neighbourhood of x with respect to the topology on X also contains a point of S other than x itself. Note that x does not have to be an element of S...
of poles and is thus not an isolated singularity. The function - is not meromorphic either, as it has an essential singularity at 0.
Properties
Since the poles of a meromorphic function are isolated, there are at most countably many. The set of poles can be infinite, as exemplified by the function
By using analytic continuation
Analytic continuation
In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which...
to eliminate removable singularities, meromorphic functions can be added, subtracted, multiplied, and the quotient
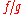can be formed unless 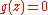on a connected componentConnected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
of D. Thus, if D is connected, the meromorphic functions form a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
, in fact a field extension
Field extension
In abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
of the complex numbers.
Meromorphic functions on Riemann surfaces
On a Riemann surfaceRiemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
every point admits an open neighborhood
which is homeomorphic
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
to an open subset of the complex plane. Thereby the notion of a meromorphic function can be defined for every Riemann surface.
When D is the entire Riemann sphere
Riemann sphere
In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
, the field of meromorphic functions is simply the field of rational functions in one variable over the complex field, since one can prove that any meromorphic function on the sphere is rational. (This is a special case of the so-called GAGA
Gaga
- Entertainment :* Lady Gaga , American recording artist* Gaga , a dancing technique* Rara, a type of Caribbean music called Gaga in the Dominican Republic* GNZ-004 Gaga, a mobile weapon in Mobile Suit Gundam 00- Sports :...
principle.)
For every Riemann surface
Riemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
, a meromorphic function is the same as a holomorphic function that maps to the Riemann sphere and which is not constant ∞. The poles correspond to those complex numbers which are mapped to ∞.
On a non-compact Riemann surface
Riemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
every meromorphic function can be realized as a quotient of two (globally defined) holomorphic functions. In contrast, on a compact Riemann surface every holomorphic function is constant, while there always exist non-constant meromorphic functions.
Meromorphic functions on an elliptic curve
Elliptic curve
In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
are also known as elliptic function
Elliptic function
In complex analysis, an elliptic function is a function defined on the complex plane that is periodic in two directions and at the same time is meromorphic...
s.
Higher dimensions
In several complex variablesSeveral complex variables
The theory of functions of several complex variables is the branch of mathematics dealing with functionson the space Cn of n-tuples of complex numbers...
, a meromorphic function is defined to be locally a quotient of two holomorphic functions. For example,
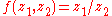is a meromorphic function on the two-dimensional complex affine space. Here it is no longer true that every meromorphic function can be regarded as holomorphic function with values in the Riemann sphereRiemann sphere
In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
: There is a set of "indeterminacy" of codimension
Codimension
In mathematics, codimension is a basic geometric idea that applies to subspaces in vector spaces, and also to submanifolds in manifolds, and suitable subsets of algebraic varieties.The dual concept is relative dimension.-Definition:...
two (in the given example this set consists of the origin
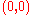).Unlike in dimension one, in higher dimensions there do exist complex manifold
Complex manifold
In differential geometry, a complex manifold is a manifold with an atlas of charts to the open unit disk in Cn, such that the transition maps are holomorphic....
s on which there are no non-constant holomorphic functions, for example, most complex tori
Complex torus
In mathematics, a complex torus is a particular kind of complex manifold M whose underlying smooth manifold is a torus in the usual sense...
.