Principal ideal domain
Encyclopedia
In abstract algebra
, a principal ideal domain, or PID, is an integral domain in which every ideal
is principal
, i.e., can be generated by a single element. More generally, a principal ideal ring
is a nonzero commutative ring whose ideals are principal, although some authors (e.g., Bourbaki) refer to PIDs as principal rings. The distinction is that a principal ideal ring may have zero divisor
s whereas a principal ideal domain cannot.
Principal ideal domains are thus mathematical objects which behave somewhat like the integers, with respect to divisibility: any element of a PID has a unique decomposition into prime elements (so an analogue of the fundamental theorem of arithmetic
holds); any two elements of a PID have a greatest common divisor
(although it may not be possible to find it using the Euclidean algorithm
). If x and y are elements of a PID without common divisors, then every element of the PID can be written in the form ax + by.
Principal ideal domains are noetherian
, they are integrally closed, they are unique factorization domain
s and Dedekind rings
. All Euclidean domain
s and all fields
are principal ideal domains.
Examples of integral domains that are not PIDs:
generated R-module, then
is a direct sum of cyclic modules, i.e., modules with one generator. The cyclic modules are isomorphic to 
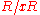for some 
.
If M is a free module over a principal ideal domain R, then every submodule of M is again free. This does not hold for modules over arbitrary rings, as the example
of modules over 
shows.
, which may be obtained as a generator of the ideal (a,b).
All Euclidean domain
s are principal ideal domains, but the converse is not true.
An example of a principal ideal domain that is not a Euclidean domain is the ring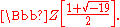
In this domain no q and r exist, with 0≤|r|<4, so that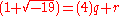
, despite 
and 4 having a greatest common divisor of 2.
Every principal ideal domain is a unique factorization domain
(UFD). The converse does not hold since for any field K, K[X,Y] is a UFD but is not a PID (to prove this look at the ideal generated by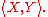
It is not the whole ring since it contains no polynomials of degree 0, but it cannot be generated by any one single element).
The previous three statements give the definition of a Dedekind domain
, and hence every principal ideal domain is a Dedekind domain.
Let A be an integral domain. Then the following are equivalent.
A field norm
is a Dedekind-Hasse norm; thus, (5) shows that a Euclidean domain is a PID. (4) compares to:
An integral domain is a Bézout domain
if and only if any two elements in it has a gcd that is a linear combination of the two. A Bézout domain is thus a GCD domain, and (4) gives yet another proof that a PID is a UFD.
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, a principal ideal domain, or PID, is an integral domain in which every ideal
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
is principal
Principal ideal
In ring theory, a branch of abstract algebra, a principal ideal is an ideal I in a ring R that is generated by a single element a of R.More specifically:...
, i.e., can be generated by a single element. More generally, a principal ideal ring
Principal ideal ring
In mathematics, a principal right ideal ring is a ring R in which every right ideal is of the form xR for some element x of R...
is a nonzero commutative ring whose ideals are principal, although some authors (e.g., Bourbaki) refer to PIDs as principal rings. The distinction is that a principal ideal ring may have zero divisor
Zero divisor
In abstract algebra, a nonzero element a of a ring is a left zero divisor if there exists a nonzero b such that ab = 0. Similarly, a nonzero element a of a ring is a right zero divisor if there exists a nonzero c such that ca = 0. An element that is both a left and a right zero divisor is simply...
s whereas a principal ideal domain cannot.
Principal ideal domains are thus mathematical objects which behave somewhat like the integers, with respect to divisibility: any element of a PID has a unique decomposition into prime elements (so an analogue of the fundamental theorem of arithmetic
Fundamental theorem of arithmetic
In number theory, the fundamental theorem of arithmetic states that any integer greater than 1 can be written as a unique product of prime numbers...
holds); any two elements of a PID have a greatest common divisor
Greatest common divisor
In mathematics, the greatest common divisor , also known as the greatest common factor , or highest common factor , of two or more non-zero integers, is the largest positive integer that divides the numbers without a remainder.For example, the GCD of 8 and 12 is 4.This notion can be extended to...
(although it may not be possible to find it using the Euclidean algorithm
Euclidean algorithm
In mathematics, the Euclidean algorithm is an efficient method for computing the greatest common divisor of two integers, also known as the greatest common factor or highest common factor...
). If x and y are elements of a PID without common divisors, then every element of the PID can be written in the form ax + by.
Principal ideal domains are noetherian
Noetherian ring
In mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element...
, they are integrally closed, they are unique factorization domain
Unique factorization domain
In mathematics, a unique factorization domain is, roughly speaking, a commutative ring in which every element, with special exceptions, can be uniquely written as a product of prime elements , analogous to the fundamental theorem of arithmetic for the integers...
s and Dedekind rings
Dedekind domain
In abstract algebra, a Dedekind domain or Dedekind ring, named after Richard Dedekind, is an integral domain in which every nonzero proper ideal factors into a product of prime ideals. It can be shown that such a factorization is then necessarily unique up to the order of the factors...
. All Euclidean domain
Euclidean domain
In mathematics, more specifically in abstract algebra and ring theory, a Euclidean domain is a ring that can be endowed with a certain structure – namely a Euclidean function, to be described in detail below – which allows a suitable generalization of the Euclidean algorithm...
s and all fields
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
are principal ideal domains.
- Commutative ringCommutative ringIn ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
s ⊃ integral domains ⊃ integrally closed domainIntegrally closed domainIn commutative algebra, an integrally closed domain A is an integral domain whose integral closure in the field of fractions of A is A itself...
s ⊃ unique factorization domainUnique factorization domainIn mathematics, a unique factorization domain is, roughly speaking, a commutative ring in which every element, with special exceptions, can be uniquely written as a product of prime elements , analogous to the fundamental theorem of arithmetic for the integers...
s ⊃ principal ideal domains ⊃ Euclidean domainEuclidean domainIn mathematics, more specifically in abstract algebra and ring theory, a Euclidean domain is a ring that can be endowed with a certain structure – namely a Euclidean function, to be described in detail below – which allows a suitable generalization of the Euclidean algorithm...
s ⊃ fieldField (mathematics)In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
s
Examples
Examples include:- K: any fieldField (mathematics)In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
, - Z: the ringRing (mathematics)In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
of integerIntegerThe integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s, - K[x]: rings of polynomialPolynomialIn mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s in one variable with coefficients in a field. (The converse is also true; that is, if A[x] is a PID, then A is a field.) Furthermore, a ring of formal power series over a field is a PID since every ideal is of the form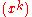
. - Z[i]: the ring of Gaussian integers
- Z[ω] (where ω is a primitive cube root of 1): the Eisenstein integers
Examples of integral domains that are not PIDs:
- Z[x]: the ring of all polynomials with integer coefficients --- it is not principal because the ideal generated by 2 and X is an example of an ideal that cannot be generated by a single polynomial.
- K[x,y]: The ideal (x,y) is not principal.
Modules
The key result is the structure theorem: If R is a principal ideal domain, and M is a finitelygenerated R-module, then
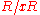is a direct sum of cyclic modules, i.e., modules with one generator. The cyclic modules are isomorphic to for some .If M is a free module over a principal ideal domain R, then every submodule of M is again free. This does not hold for modules over arbitrary rings, as the example
of modules over shows.Properties
In a principal ideal domain, any two elements a,b have a greatest common divisorGreatest common divisor
In mathematics, the greatest common divisor , also known as the greatest common factor , or highest common factor , of two or more non-zero integers, is the largest positive integer that divides the numbers without a remainder.For example, the GCD of 8 and 12 is 4.This notion can be extended to...
, which may be obtained as a generator of the ideal (a,b).
All Euclidean domain
Euclidean domain
In mathematics, more specifically in abstract algebra and ring theory, a Euclidean domain is a ring that can be endowed with a certain structure – namely a Euclidean function, to be described in detail below – which allows a suitable generalization of the Euclidean algorithm...
s are principal ideal domains, but the converse is not true.
An example of a principal ideal domain that is not a Euclidean domain is the ring
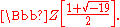
In this domain no q and r exist, with 0≤|r|<4, so that
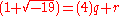, despite and 4 having a greatest common divisor of 2.Every principal ideal domain is a unique factorization domain
Unique factorization domain
In mathematics, a unique factorization domain is, roughly speaking, a commutative ring in which every element, with special exceptions, can be uniquely written as a product of prime elements , analogous to the fundamental theorem of arithmetic for the integers...
(UFD). The converse does not hold since for any field K, K[X,Y] is a UFD but is not a PID (to prove this look at the ideal generated by
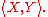It is not the whole ring since it contains no polynomials of degree 0, but it cannot be generated by any one single element).- Every principal ideal domain is NoetherianNoetherian ringIn mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element...
. - In all unital rings, maximal idealMaximal idealIn mathematics, more specifically in ring theory, a maximal ideal is an ideal which is maximal amongst all proper ideals. In other words, I is a maximal ideal of a ring R if I is an ideal of R, I ≠ R, and whenever J is another ideal containing I as a subset, then either J = I or J = R...
s are primePrime idealIn algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...
. In principal ideal domains a near converse holds: every nonzero prime ideal is maximal. - All principal ideal domains are integrally closedIntegrally closedIn mathematics, more specifically in abstract algebra, the concept of integrally closed has two meanings, one for groups and one for rings. -Commutative rings:...
.
The previous three statements give the definition of a Dedekind domain
Dedekind domain
In abstract algebra, a Dedekind domain or Dedekind ring, named after Richard Dedekind, is an integral domain in which every nonzero proper ideal factors into a product of prime ideals. It can be shown that such a factorization is then necessarily unique up to the order of the factors...
, and hence every principal ideal domain is a Dedekind domain.
Let A be an integral domain. Then the following are equivalent.
- A is a PID.
- Every prime ideal of A is principal.
- A is a Dedekind domain that is a UFD.
- Every finitely generated ideal of A is principal (i.e., A is a Bézout domainBézout domainIn mathematics, a Bézout domain is an integral domain in which the sum of two principal ideals is again a principal ideal. This means that for every pair of elements a Bézout identity holds, and that every finitely generated ideal is principal...
) and A satisfies the ascending chain condition on principal idealsAscending chain condition on principal idealsIn abstract algebra, the ascending chain condition can be applied to the posets of principal left, principal right, or principal two-sided ideals of a ring, partially ordered by inclusion...
. - A admits a Dedekind–Hasse normDedekind–Hasse normIn mathematics, in particular the study of abstract algebra, a Dedekind–Hasse norm is a function on an integral domain that generalises the notion of a Euclidean function on Euclidean domains.-Definition:...
.
A field norm
Field norm
In mathematics, the norm is a mapping defined in field theory, to map elements of a larger field into a smaller one.-Formal definitions:1. Let K be a field and L a finite extension of K...
is a Dedekind-Hasse norm; thus, (5) shows that a Euclidean domain is a PID. (4) compares to:
- An integral domain is a UFD if and only if it is a GCD domainGCD domainIn mathematics, a GCD domain is an integral domain R with the property that any two non-zero elements have a greatest common divisor . Equivalently, any two non-zero elements of R have a least common multiple ....
(i.e., a domain where every two elements has a greatest common divisor) satisfying the ascending chain condition on principal ideals.
An integral domain is a Bézout domain
Bézout domain
In mathematics, a Bézout domain is an integral domain in which the sum of two principal ideals is again a principal ideal. This means that for every pair of elements a Bézout identity holds, and that every finitely generated ideal is principal...
if and only if any two elements in it has a gcd that is a linear combination of the two. A Bézout domain is thus a GCD domain, and (4) gives yet another proof that a PID is a UFD.
External links
- Principal ring on MathWorldMathWorldMathWorld is an online mathematics reference work, created and largely written by Eric W. Weisstein. It is sponsored by and licensed to Wolfram Research, Inc. and was partially funded by the National Science Foundation's National Science Digital Library grant to the University of Illinois at...