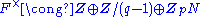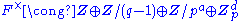Local field
Encyclopedia
In mathematics
, a local field is a special type of field
that is a locally compact topological field with respect to a non-discrete topology
.
Given such a field, an absolute value
can be defined on it. There are two basic types of local field: those in which the absolute value is archimedean
and those in which it is not. In the first case, one calls the local field an archimedean local field, in the second case, one calls it a non-archimedean local field. Local fields arise naturally in number theory
as completions of global field
s.
Every local field is isomorphic (as a topological field) to one of the following:
There is an equivalent definition of non-archimedean local field: it is a field that is complete with respect to a discrete valuation and whose residue field
is finite. However, some authors consider a more general notion, requiring only that the residue field be perfect
, not necessarily finite. This article uses the former definition.
, it has a unique (up to positive scalar multiple) Haar measure
μ. The absolute value is defined so as to measure the change in size of a set after multiplying it by an element of K. Specifically, define |·| : K → R by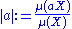
for any measurable subset X of K (with 0 < μ(X) < ∞). This absolute value does not depend on X nor on the choice of Haar measure (since the same scalar multiple ambiguity will occur in both the numerator and the denominator).
Given such an absolute value on K, a new induced topology can be defined on K. This topology is the same as the original topology. Explicitly, for a positive real number m, define the subset Bm of K by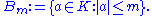
Then, the Bm make up a neighbourhood basis of 0 in K.
Every non-zero element a of F can be written as a = ϖnu with u a unit, and n a unique integer.
The normalized valuation of F is the surjective function
v : F → Z ∪ {∞} defined by sending a non-zero a to the unique integer n such that a = ϖnu with u a unit, and by sending 0 to ∞. If q is the cardinality of the residue field, the absolute value on F induced by its structure as a local field is given by
An equivalent definition of a non-archimedean local field is that it is a field that is complete with respect to a discrete valuation and whose residue field is finite.
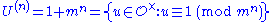
for n ≥ 1. The group U(1) is called the group of principal units, and any element of it is called a principal unit. The full unit group is denoted U(0).
is denoted U(0).
The higher unit groups provide a decreasing filtration of the unit group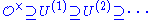
whose quotients
are given by
for n ≥ 1. (Here " " means a non-canonical isomorphism.)
" means a non-canonical isomorphism.)

where q is the order of the residue field, and μq−1 is the group of (q−1)st roots of unity (in F). Its structure as an abelian group depends on its characteristic
:
For a non-negative integer n, an n-dimensional local field is a complete discrete valuation field whose residue field is an (n − 1)-dimensional local field. Depending on the definition of local field, a zero-dimensional local field is then either a finite field (with the definition used in this article), or a quasi-finite field
, or a perfect field.
From the geometric point of view, n-dimensional local fields with last finite residue field are naturally associated to a complete flag of subschemes of an n-dimensional arithmetic scheme.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a local field is a special type of field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
that is a locally compact topological field with respect to a non-discrete topology
Discrete space
In topology, a discrete space is a particularly simple example of a topological space or similar structure, one in which the points are "isolated" from each other in a certain sense.- Definitions :Given a set X:...
.
Given such a field, an absolute value
Absolute value (algebra)
In mathematics, an absolute value is a function which measures the "size" of elements in a field or integral domain. More precisely, if D is an integral domain, then an absolute value is any mapping | x | from D to the real numbers R satisfying:* | x | ≥ 0,*...
can be defined on it. There are two basic types of local field: those in which the absolute value is archimedean
Archimedean property
In abstract algebra and analysis, the Archimedean property, named after the ancient Greek mathematician Archimedes of Syracuse, is a property held by some ordered or normed groups, fields, and other algebraic structures. Roughly speaking, it is the property of having no infinitely large or...
and those in which it is not. In the first case, one calls the local field an archimedean local field, in the second case, one calls it a non-archimedean local field. Local fields arise naturally in number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
as completions of global field
Global field
In mathematics, the term global field refers to either of the following:*an algebraic number field, i.e., a finite extension of Q, or*a global function field, i.e., the function field of an algebraic curve over a finite field, equivalently, a finite extension of Fq, the field of rational functions...
s.
Every local field is isomorphic (as a topological field) to one of the following:
- Archimedean local fields (characteristicCharacteristic (algebra)In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
zero): the real numbers R, and the complex numbers C. - Non-archimedean local fields of characteristic zero: finite extensions of the p-adic numberP-adic numberIn mathematics, and chiefly number theory, the p-adic number system for any prime number p extends the ordinary arithmetic of the rational numbers in a way different from the extension of the rational number system to the real and complex number systems...
s Qp (where p is any prime numberPrime numberA prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
). - Non-archimedean local fields of characteristic p (for p any given prime number): the field of formal Laurent series Fq((T)) over a finite fieldFinite fieldIn abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
Fq (where q is a powerExponentiationExponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
of p).
There is an equivalent definition of non-archimedean local field: it is a field that is complete with respect to a discrete valuation and whose residue field
Residue field
In mathematics, the residue field is a basic construction in commutative algebra. If R is a commutative ring and m is a maximal ideal, then the residue field is the quotient ring k = R/m, which is a field...
is finite. However, some authors consider a more general notion, requiring only that the residue field be perfect
Perfect field
In algebra, a field k is said to be perfect if any one of the following equivalent conditions holds:* Every irreducible polynomial over k has distinct roots.* Every polynomial over k is separable.* Every finite extension of k is separable...
, not necessarily finite. This article uses the former definition.
Induced absolute value
Given a locally compact topological field K, an absolute value can be defined as follows. First, consider the additive group of the field. As a locally compact topological groupTopological group
In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
, it has a unique (up to positive scalar multiple) Haar measure
Haar measure
In mathematical analysis, the Haar measure is a way to assign an "invariant volume" to subsets of locally compact topological groups and subsequently define an integral for functions on those groups....
μ. The absolute value is defined so as to measure the change in size of a set after multiplying it by an element of K. Specifically, define |·| : K → R by
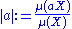
for any measurable subset X of K (with 0 < μ(X) < ∞). This absolute value does not depend on X nor on the choice of Haar measure (since the same scalar multiple ambiguity will occur in both the numerator and the denominator).
Given such an absolute value on K, a new induced topology can be defined on K. This topology is the same as the original topology. Explicitly, for a positive real number m, define the subset Bm of K by
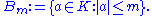
Then, the Bm make up a neighbourhood basis of 0 in K.
Non-archimedean local field theory
For a non-archimedean local field F (with absolute value denoted by |·|), the following objects are important:- its ring of integersRing of integersIn mathematics, the ring of integers is the set of integers making an algebraic structure Z with the operations of integer addition, negation, and multiplication...
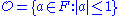 which is a discrete valuation ringDiscrete valuation ringIn abstract algebra, a discrete valuation ring is a principal ideal domain with exactly one non-zero maximal ideal.This means a DVR is an integral domain R which satisfies any one of the following equivalent conditions:...
which is a discrete valuation ringDiscrete valuation ringIn abstract algebra, a discrete valuation ring is a principal ideal domain with exactly one non-zero maximal ideal.This means a DVR is an integral domain R which satisfies any one of the following equivalent conditions:...
, is the closed unit ball of F, and is compactCompact spaceIn mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
; - the units in its ring of integers
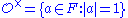 which forms a groupGroup (mathematics)In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
which forms a groupGroup (mathematics)In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
and is the unit sphereUnit sphereIn mathematics, a unit sphere is the set of points of distance 1 from a fixed central point, where a generalized concept of distance may be used; a closed unit ball is the set of points of distance less than or equal to 1 from a fixed central point...
of F; - the unique non-zero prime idealPrime idealIn algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...
 in its ring of integers which is its open unit ball
in its ring of integers which is its open unit ball 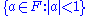 ;
; - a generatorPrincipal idealIn ring theory, a branch of abstract algebra, a principal ideal is an ideal I in a ring R that is generated by a single element a of R.More specifically:...
ϖ of called a uniformizer of F;
called a uniformizer of F; - its residue field
 which is finite (since it is compact and discreteDiscrete spaceIn topology, a discrete space is a particularly simple example of a topological space or similar structure, one in which the points are "isolated" from each other in a certain sense.- Definitions :Given a set X:...
which is finite (since it is compact and discreteDiscrete spaceIn topology, a discrete space is a particularly simple example of a topological space or similar structure, one in which the points are "isolated" from each other in a certain sense.- Definitions :Given a set X:...
).
Every non-zero element a of F can be written as a = ϖnu with u a unit, and n a unique integer.
The normalized valuation of F is the surjective function
Surjective function
In mathematics, a function f from a set X to a set Y is surjective , or a surjection, if every element y in Y has a corresponding element x in X so that f = y...
v : F → Z ∪ {∞} defined by sending a non-zero a to the unique integer n such that a = ϖnu with u a unit, and by sending 0 to ∞. If q is the cardinality of the residue field, the absolute value on F induced by its structure as a local field is given by

An equivalent definition of a non-archimedean local field is that it is a field that is complete with respect to a discrete valuation and whose residue field is finite.
Examples
- The p-adic numbers: the ring of integers of Qp is the ring of p-adic integers Zp. Its prime ideal is pZp and its residue field is Z/pZ. Every non-zero element of Qp can be written as u pn where u is a unit in Zp and n is an integer, then v(u pn) = n for the normalized valuation.
- The formal Laurent series over a finite field: the ring of integers of Fq((T)) is the ring of formal power seriesFormal power seriesIn mathematics, formal power series are a generalization of polynomials as formal objects, where the number of terms is allowed to be infinite; this implies giving up the possibility to substitute arbitrary values for indeterminates...
FqT . Its prime ideal is (T) (i.e. the power series whose constant term Constant termIn mathematics, a constant term is a term in an algebraic expression has a value that is constant or cannot change, because it does not contain any modifiable variables. For example, in the quadratic polynomialx^2 + 2x + 3,\ the 3 is a constant term....
is zero) and its residue field is Fq. Its normalized valuation is related to the (lower) degree of a formal Laurent series as follows:-
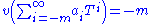 (where a−m is non-zero).
(where a−m is non-zero).
-
- The formal Laurent series over the complex numbers is not a local field. For example, its residue field is C
T /(T) = C, which is not finite.
Higher unit groups
The nth higher unit group of a non-archimedean local field F is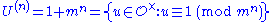
for n ≥ 1. The group U(1) is called the group of principal units, and any element of it is called a principal unit. The full unit group
 is denoted U(0).
is denoted U(0).The higher unit groups provide a decreasing filtration of the unit group
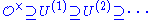
whose quotients
Quotient group
In mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
are given by

for n ≥ 1. (Here "
 " means a non-canonical isomorphism.)
" means a non-canonical isomorphism.)Structure of the unit group
The multiplicative group of non-zero elements of a non-archimedean local field F is isomorphic to
where q is the order of the residue field, and μq−1 is the group of (q−1)st roots of unity (in F). Its structure as an abelian group depends on its characteristic
Characteristic (algebra)
In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
:
- If F has positive characteristic p, then
-
- where N denotes the natural numberNatural numberIn mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s;- If F has characteristic zero (i.e. it is a finite extension of Qp of degree d), then
- where a ≥ 0 is defined so that the group of p-power roots of unity in F is
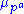 .
.
Higher dimensional local fields
It is natural to introduce non-archimedean local fields in a uniform geometric way as the field of fractions of the completion of the local ring of a one-dimensional arithmetic scheme of rank 1 at its non-singular point. For generalizations, a local field is sometimes called a one-dimensional local field.For a non-negative integer n, an n-dimensional local field is a complete discrete valuation field whose residue field is an (n − 1)-dimensional local field. Depending on the definition of local field, a zero-dimensional local field is then either a finite field (with the definition used in this article), or a quasi-finite field
Quasi-finite field
In mathematics, a quasi-finite field is a generalisation of a finite field. Standard local class field theory usually deals with complete valued fields whose residue field is finite In mathematics, a quasi-finite field is a generalisation of a finite field. Standard local class field theory usually...
, or a perfect field.
From the geometric point of view, n-dimensional local fields with last finite residue field are naturally associated to a complete flag of subschemes of an n-dimensional arithmetic scheme.
Further reading
- A. Frohlich, "Local fields", in J.W.S. Cassels and A. Frohlich (edd), Algebraic number theory, Academic PressAcademic PressAcademic Press is an academic book publisher. Originally independent, it was acquired by Harcourt, Brace & World in 1969. Reed Elsevier bought Harcourt in 2000, and Academic Press is now an imprint of Elsevier....
, 1973. Chap.I - Milne, James, Algebraic Number Theory.
- Schikhoff, W.H. (1984) Ultrametric Calculus