
Characteristic (algebra)
Encyclopedia
In mathematics
, the characteristic of a ring
R, often denoted char(R), is defined to be the smallest number of times one must use the ring's multiplicative identity element
(1) in a sum to get the additive identity
element (0); the ring is said to have characteristic zero if this repeated sum never reaches the additive identity.
That is, char(R) is the smallest positive number n such that
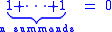
if such a number n exists, and 0 otherwise.
The characteristic may also be taken to be the exponent of the ring's additive group, that is, the smallest positive n such that
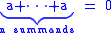
for every element a of the ring (again, if n exists; otherwise zero). Some authors do not include the multiplicative identity element in their requirements for a ring (see ring), and this definition is suitable for that convention; otherwise the two definitions are easily seen to be equivalent due to the distributive law in rings.
Other equivalent definitions include taking the characteristic to be the natural number
n such that nZ is the kernel of a ring homomorphism
from Z to R, or such that R contains a subring
isomorphic
to the factor ring Z/nZ, which would be the image
of that homomorphism. The requirements of ring homomorphisms are such that there can be only one homomorphism from the ring of integers to any ring; in the language of category theory
, Z is an initial object
of the category of rings
. Again this follows the convention that a ring has a multiplicative identity element (which is preserved by ring homomorphisms).
R → S, then the characteristic of S divides the characteristic of R. This can sometimes be used to exclude the possibility of certain ring homomorphisms. The only ring with characteristic 1 is the trivial ring which has only a single element 0=1. If the non-trivial ring R does not have any zero divisor
s, then its characteristic is either 0 or prime
. In particular, this applies to all fields
, to all integral domains, and to all division ring
s. Any ring of characteristic 0 is infinite.
The ring Z/nZ of integers modulo
n has characteristic n. If R is a subring
of S, then R and S have the same characteristic. For instance, if q(X) is a prime polynomial
with coefficients in the field Z/pZ where p is prime, then the factor ring (Z/pZ)[X]/(q(X)) is a field of characteristic p. Since the complex number
s contain the rationals, their characteristic is 0.
If a commutative ring R has prime characteristic p, then we have (x + y)p = xp + yp for all elements x and y in R – the "freshman's dream
" holds for power p.
The map
then defines a ring homomorphism
It is called the Frobenius homomorphism. If R is an integral domain it is injective.
For any field F, there is a minimal subfield, namely the , the smallest subfield containing 1F. It is isomorphic either to the rational number
field Q, or a finite field of prime order, Fp; the structure of the prime field and the characteristic each determine the other. Fields of characteristic zero have the most familiar properties; for practical purposes they resemble subfields of the complex number
s (unless they have very large cardinality, that is; in fact, any field of characteristic zero and cardinality at most continuum
is isomorphic to a subfield of complex numbers). The p-adic fields are characteristic zero fields, much applied in number theory, that are constructed from rings of characteristic pk, as k → ∞.
For any ordered field
(for example, the rationals
or the reals
) the characteristic is 0. The finite field
GF(pn) has characteristic p. There exist infinite fields of prime characteristic. For example, the field of all rational function
s over Z/pZ is one such. The algebraic closure
of Z/pZ is another example.
The size of any finite ring
of prime characteristic p is a power of p. Since in that case it must contain Z/pZ it must also be a vector space
over that field and from linear algebra
we know that the sizes of finite vector spaces over finite fields are a power of the size of the field. This also shows that the size of any finite vector space is a prime power. (It is a vector space over a finite field, which we have shown to be of size pn. So its size is (pn)m = pnm.)
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the characteristic of a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
R, often denoted char(R), is defined to be the smallest number of times one must use the ring's multiplicative identity element
Identity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
(1) in a sum to get the additive identity
Additive identity
In mathematics the additive identity of a set which is equipped with the operation of addition is an element which, when added to any element x in the set, yields x...
element (0); the ring is said to have characteristic zero if this repeated sum never reaches the additive identity.
That is, char(R) is the smallest positive number n such that
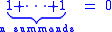
if such a number n exists, and 0 otherwise.
The characteristic may also be taken to be the exponent of the ring's additive group, that is, the smallest positive n such that
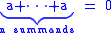
for every element a of the ring (again, if n exists; otherwise zero). Some authors do not include the multiplicative identity element in their requirements for a ring (see ring), and this definition is suitable for that convention; otherwise the two definitions are easily seen to be equivalent due to the distributive law in rings.
Other equivalent definitions include taking the characteristic to be the natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
n such that nZ is the kernel of a ring homomorphism
Ring homomorphism
In ring theory or abstract algebra, a ring homomorphism is a function between two rings which respects the operations of addition and multiplication....
from Z to R, or such that R contains a subring
Subring
In mathematics, a subring of R is a subset of a ring, is itself a ring with the restrictions of the binary operations of addition and multiplication of R, and which contains the multiplicative identity of R...
isomorphic
Ring homomorphism
In ring theory or abstract algebra, a ring homomorphism is a function between two rings which respects the operations of addition and multiplication....
to the factor ring Z/nZ, which would be the image
Image (mathematics)
In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
of that homomorphism. The requirements of ring homomorphisms are such that there can be only one homomorphism from the ring of integers to any ring; in the language of category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, Z is an initial object
Initial object
In category theory, an abstract branch of mathematics, an initial object of a category C is an object I in C such that for every object X in C, there exists precisely one morphism I → X...
of the category of rings
Category of rings
In mathematics, the category of rings, denoted by Ring, is the category whose objects are rings and whose morphisms are ring homomorphisms...
. Again this follows the convention that a ring has a multiplicative identity element (which is preserved by ring homomorphisms).
Case of rings
If R and S are rings and there exists a ring homomorphismRing homomorphism
In ring theory or abstract algebra, a ring homomorphism is a function between two rings which respects the operations of addition and multiplication....
R → S, then the characteristic of S divides the characteristic of R. This can sometimes be used to exclude the possibility of certain ring homomorphisms. The only ring with characteristic 1 is the trivial ring which has only a single element 0=1. If the non-trivial ring R does not have any zero divisor
Zero divisor
In abstract algebra, a nonzero element a of a ring is a left zero divisor if there exists a nonzero b such that ab = 0. Similarly, a nonzero element a of a ring is a right zero divisor if there exists a nonzero c such that ca = 0. An element that is both a left and a right zero divisor is simply...
s, then its characteristic is either 0 or prime
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
. In particular, this applies to all fields
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
, to all integral domains, and to all division ring
Division ring
In abstract algebra, a division ring, also called a skew field, is a ring in which division is possible. Specifically, it is a non-trivial ring in which every non-zero element a has a multiplicative inverse, i.e., an element x with...
s. Any ring of characteristic 0 is infinite.
The ring Z/nZ of integers modulo
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
n has characteristic n. If R is a subring
Subring
In mathematics, a subring of R is a subset of a ring, is itself a ring with the restrictions of the binary operations of addition and multiplication of R, and which contains the multiplicative identity of R...
of S, then R and S have the same characteristic. For instance, if q(X) is a prime polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
with coefficients in the field Z/pZ where p is prime, then the factor ring (Z/pZ)[X]/(q(X)) is a field of characteristic p. Since the complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s contain the rationals, their characteristic is 0.
If a commutative ring R has prime characteristic p, then we have (x + y)p = xp + yp for all elements x and y in R – the "freshman's dream
Freshman's dream
The freshman's dream is a name sometimes given to the error n = xn + yn, where n is a real number . Beginning students commonly make this error in computing the exponential of a sum of real numbers...
" holds for power p.
The map
then defines a ring homomorphism
Ring homomorphism
In ring theory or abstract algebra, a ring homomorphism is a function between two rings which respects the operations of addition and multiplication....
It is called the Frobenius homomorphism. If R is an integral domain it is injective.
Case of fields
As mentioned above, the characteristic of any field is either 0 or a prime number.For any field F, there is a minimal subfield, namely the , the smallest subfield containing 1F. It is isomorphic either to the rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
field Q, or a finite field of prime order, Fp; the structure of the prime field and the characteristic each determine the other. Fields of characteristic zero have the most familiar properties; for practical purposes they resemble subfields of the complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s (unless they have very large cardinality, that is; in fact, any field of characteristic zero and cardinality at most continuum
Cardinality of the continuum
In set theory, the cardinality of the continuum is the cardinality or “size” of the set of real numbers \mathbb R, sometimes called the continuum. It is an infinite cardinal number and is denoted by |\mathbb R| or \mathfrak c ....
is isomorphic to a subfield of complex numbers). The p-adic fields are characteristic zero fields, much applied in number theory, that are constructed from rings of characteristic pk, as k → ∞.
For any ordered field
Ordered field
In mathematics, an ordered field is a field together with a total ordering of its elements that is compatible with the field operations. Historically, the axiomatization of an ordered field was abstracted gradually from the real numbers, by mathematicians including David Hilbert, Otto Hölder and...
(for example, the rationals
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
or the reals
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
) the characteristic is 0. The finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
GF(pn) has characteristic p. There exist infinite fields of prime characteristic. For example, the field of all rational function
Rational function
In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
s over Z/pZ is one such. The algebraic closure
Algebraic closure
In mathematics, particularly abstract algebra, an algebraic closure of a field K is an algebraic extension of K that is algebraically closed. It is one of many closures in mathematics....
of Z/pZ is another example.
The size of any finite ring
Finite ring
In mathematics, more specifically abstract algebra, a finite ring is a ring that has a finite number of elements....
of prime characteristic p is a power of p. Since in that case it must contain Z/pZ it must also be a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
over that field and from linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
we know that the sizes of finite vector spaces over finite fields are a power of the size of the field. This also shows that the size of any finite vector space is a prime power. (It is a vector space over a finite field, which we have shown to be of size pn. So its size is (pn)m = pnm.)

