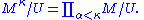Ultraproduct
Encyclopedia
The ultraproduct is a mathematical
construction that appears mainly in abstract algebra
and in model theory
, a branch of mathematical logic
. An ultraproduct is a quotient of the direct product of a family of structures
. All factors need to have the same signature
. The ultrapower is the special case of this construction in which all factors are equal.
For example, ultrapowers can be used to construct new field
s from given ones. The hyperreal numbers, an ultrapower of the real numbers, are a special case of this.
Some striking applications of ultraproducts include very elegant proofs of the compactness theorem
and the completeness theorem, Keisler's ultrapower theorem, which gives an algebraic characterization of the semantic notion of elementary equivalence, and the Robinson-Zakon presentation of the use of superstructures and their monomorphisms to construct nonstandard models of analysis, leading to the growth of the area of nonstandard analysis, which was pioneered (as an application of the compactness theorem) by Abraham Robinson
.
Mi for each element i of I (all of the same signature
), and an ultrafilter
U on I. The usual choice is for I to be infinite and U to contain all cofinite
subsets of I. Otherwise the ultrafilter is principal, and the ultraproduct is isomorphic to one of the factors.
Algebraic operations on the Cartesian product
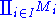
are defined in the usual way (for example, for a binary function +, (a + b) i = ai + bi ), and an equivalence relation
is defined by a ~ b if and only if
and the ultraproduct is the quotient set with respect to ~. The ultraproduct is therefore sometimes denoted by
One may define a finitely additive measure
m on the index set I by saying m(A) = 1 if A ∈ U and = 0 otherwise. Then two members of the Cartesian product are equivalent precisely if they are equal almost everywhere
on the index set. The ultraproduct is the set of equivalence classes thus generated.
Other relation
s can be extended the same way:
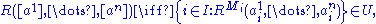
where [a] denotes the equivalence class of a with respect to ~.
In particular, if every Mi is an ordered field
, then so is the ultraproduct.
An ultrapower is an ultraproduct for which all the factors Mi are equal:
More generally, the construction above can be carried out whenever U is a filter
on I; the resulting model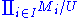
is then called a reduced product.
Analogously, one can define nonstandard integers, nonstandard complex numbers, etc., by taking the ultraproduct of copies of the corresponding structures.
As an example of the carrying over of relations into the ultraproduct, consider the sequence ψ defined by ψi = 2i. Because ψi > ωi = i for all i, it follows that the equivalence class of ψi = 2i is greater than the equivalence class of ωi = i, so that it can be interpreted as an infinite number which is greater than the one originally constructed. However, let χi = i for i not equal to 7, but χ7 = 8. The set of indices on which ω and χ agree is a member of any ultrafilter (because ω and χ agree almost everywhere), so ω and χ belong to the same equivalence class.
In the theory of large cardinals, a standard construction is to take the ultraproduct of the whole set-theoretic universe with respect to some carefully chosen ultrafilter U. Properties of this ultrafilter U have a strong influence on (higher order) properties of the ultraproduct; for example, if U is σ-complete, then the ultraproduct will again be well-founded. (See measurable cardinal
for the prototypical example.)
Let σ be a signature,
an ultrafilter over a set 
, and for each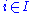 
let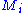 
be a σ-structure. Let 
be the ultraproduct of the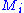 
with respect to 
, that is, 
Then, for each 
, where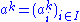 
, and for every σ-formula 
,
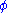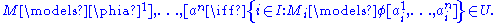
The theorem is proved by induction on the complexity of the formula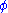
. The fact that 
is an ultrafilter (and not just a filter) is used in the negation clause, and the axiom of choice is needed at the existential quantifier step. As an application, one obtains the transfer theorem
for hyperreal fields
.
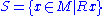has an analog *S in the ultrapower, and first-order formulas involving S are also valid for *S. For example, let M be the reals, and let Rx hold if x is a rational number. Then in M we can say that for any pair of rationals x and y, there exists another number z such that z is not rational, and x < z < y. Since this can be translated into a first-order logical formula in the relevant formal language, Łoś's theorem implies that *S has the same property. That is, we can define a notion of the hyperrational numbers, which are a subset of the hyperreals, and they have the same first-order properties as the rationals.
Consider, however, the Archimedean property
of the reals, which states that there is no real number x such that x > 1, x > 1 +1 , x > 1 + 1 + 1, ... for every inequality in the infinite list. Łoś's theorem does not apply to the Archimedean property, because the Archimedean property cannot be stated in first-order logic. In fact, the Archimedean property is false for the hyperreals, as shown by the construction of the hyperreal number ω above.
In model theory
and set theory
, an ultralimit or limiting ultrapower is a direct limit
of a sequence of ultrapowers.
Beginning with a structure, A0, and an ultrafilter, D0, form an ultrapower, A1. Then repeat the process to form A2, and so forth. For each n there is a canonical diagonal embedding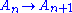
. At limit stages, such as Aω, form the direct limit of earlier stages. One may continue into the transfinite.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
construction that appears mainly in abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
and in model theory
Model theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
, a branch of mathematical logic
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
. An ultraproduct is a quotient of the direct product of a family of structures
Structure (mathematical logic)
In universal algebra and in model theory, a structure consists of a set along with a collection of finitary operations and relations which are defined on it....
. All factors need to have the same signature
Signature (logic)
In logic, especially mathematical logic, a signature lists and describes the non-logical symbols of a formal language. In universal algebra, a signature lists the operations that characterize an algebraic structure. In model theory, signatures are used for both purposes.Signatures play the same...
. The ultrapower is the special case of this construction in which all factors are equal.
For example, ultrapowers can be used to construct new field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
s from given ones. The hyperreal numbers, an ultrapower of the real numbers, are a special case of this.
Some striking applications of ultraproducts include very elegant proofs of the compactness theorem
Compactness theorem
In mathematical logic, the compactness theorem states that a set of first-order sentences has a model if and only if every finite subset of it has a model...
and the completeness theorem, Keisler's ultrapower theorem, which gives an algebraic characterization of the semantic notion of elementary equivalence, and the Robinson-Zakon presentation of the use of superstructures and their monomorphisms to construct nonstandard models of analysis, leading to the growth of the area of nonstandard analysis, which was pioneered (as an application of the compactness theorem) by Abraham Robinson
Abraham Robinson
Abraham Robinson was a mathematician who is most widely known for development of non-standard analysis, a mathematically rigorous system whereby infinitesimal and infinite numbers were incorporated into mathematics....
.
Definition
The general method for getting ultraproducts uses an index set I, a structureStructure (mathematical logic)
In universal algebra and in model theory, a structure consists of a set along with a collection of finitary operations and relations which are defined on it....
Mi for each element i of I (all of the same signature
Signature (logic)
In logic, especially mathematical logic, a signature lists and describes the non-logical symbols of a formal language. In universal algebra, a signature lists the operations that characterize an algebraic structure. In model theory, signatures are used for both purposes.Signatures play the same...
), and an ultrafilter
Ultrafilter
In the mathematical field of set theory, an ultrafilter on a set X is a collection of subsets of X that is a filter, that cannot be enlarged . An ultrafilter may be considered as a finitely additive measure. Then every subset of X is either considered "almost everything" or "almost nothing"...
U on I. The usual choice is for I to be infinite and U to contain all cofinite
Cofinite
In mathematics, a cofinite subset of a set X is a subset A whose complement in X is a finite set. In other words, A contains all but finitely many elements of X...
subsets of I. Otherwise the ultrafilter is principal, and the ultraproduct is isomorphic to one of the factors.
Algebraic operations on the Cartesian product
Cartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
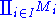
are defined in the usual way (for example, for a binary function +, (a + b) i = ai + bi ), and an equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
is defined by a ~ b if and only if
and the ultraproduct is the quotient set with respect to ~. The ultraproduct is therefore sometimes denoted by
One may define a finitely additive measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
m on the index set I by saying m(A) = 1 if A ∈ U and = 0 otherwise. Then two members of the Cartesian product are equivalent precisely if they are equal almost everywhere
Almost everywhere
In measure theory , a property holds almost everywhere if the set of elements for which the property does not hold is a null set, that is, a set of measure zero . In cases where the measure is not complete, it is sufficient that the set is contained within a set of measure zero...
on the index set. The ultraproduct is the set of equivalence classes thus generated.
Other relation
Relation (mathematics)
In set theory and logic, a relation is a property that assigns truth values to k-tuples of individuals. Typically, the property describes a possible connection between the components of a k-tuple...
s can be extended the same way:
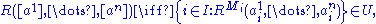
where [a] denotes the equivalence class of a with respect to ~.
In particular, if every Mi is an ordered field
Ordered field
In mathematics, an ordered field is a field together with a total ordering of its elements that is compatible with the field operations. Historically, the axiomatization of an ordered field was abstracted gradually from the real numbers, by mathematicians including David Hilbert, Otto Hölder and...
, then so is the ultraproduct.
An ultrapower is an ultraproduct for which all the factors Mi are equal:
More generally, the construction above can be carried out whenever U is a filter
Filter (mathematics)
In mathematics, a filter is a special subset of a partially ordered set. A frequently used special case is the situation that the ordered set under consideration is just the power set of some set, ordered by set inclusion. Filters appear in order and lattice theory, but can also be found in...
on I; the resulting model
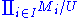is then called a reduced product.Examples
The hyperreal numbers are the ultraproduct of one copy of the real numbers for every natural number, with regard to an ultrafilter over the natural numbers containing all cofinite sets. Their order is the extension of the order of the real numbers. For example, the sequence ω given by ωi = i defines an equivalence class representing a hyperreal number that is greater than any real number.Analogously, one can define nonstandard integers, nonstandard complex numbers, etc., by taking the ultraproduct of copies of the corresponding structures.
As an example of the carrying over of relations into the ultraproduct, consider the sequence ψ defined by ψi = 2i. Because ψi > ωi = i for all i, it follows that the equivalence class of ψi = 2i is greater than the equivalence class of ωi = i, so that it can be interpreted as an infinite number which is greater than the one originally constructed. However, let χi = i for i not equal to 7, but χ7 = 8. The set of indices on which ω and χ agree is a member of any ultrafilter (because ω and χ agree almost everywhere), so ω and χ belong to the same equivalence class.
In the theory of large cardinals, a standard construction is to take the ultraproduct of the whole set-theoretic universe with respect to some carefully chosen ultrafilter U. Properties of this ultrafilter U have a strong influence on (higher order) properties of the ultraproduct; for example, if U is σ-complete, then the ultraproduct will again be well-founded. (See measurable cardinal
Measurable cardinal
- Measurable :Formally, a measurable cardinal is an uncountable cardinal number κ such that there exists a κ-additive, non-trivial, 0-1-valued measure on the power set of κ...
for the prototypical example.)
Łoś's theorem
Łoś's theorem, also called the fundamental theorem of ultraproducts, is due to Jerzy Łoś (the surname is pronounced ˈwɔɕ, approximately "wash"). It states that any first-order formula is true in the ultraproduct if and only if the set of indices i such that the formula is true in Mi is a member of U. More precisely:Let σ be a signature,
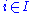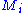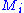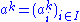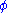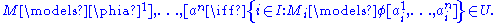
an ultrafilter over a set , and for each let be a σ-structure. Let be the ultraproduct of the with respect to , that is, Then, for each , where , and for every σ-formula ,The theorem is proved by induction on the complexity of the formula
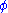. The fact that is an ultrafilter (and not just a filter) is used in the negation clause, and the axiom of choice is needed at the existential quantifier step. As an application, one obtains the transfer theoremTransfer principle
In model theory, a transfer principle states that all statements of some language that are true for some structure are true for another structure...
for hyperreal fields
Hyperreal number
The system of hyperreal numbers represents a rigorous method of treating the infinite and infinitesimal quantities. The hyperreals, or nonstandard reals, *R, are an extension of the real numbers R that contains numbers greater than anything of the form1 + 1 + \cdots + 1. \, Such a number is...
.
Examples
Let R be a unary relation in the structure M, and form the ultrapower of M. Then the set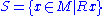 has an analog *S in the ultrapower, and first-order formulas involving S are also valid for *S. For example, let M be the reals, and let Rx hold if x is a rational number. Then in M we can say that for any pair of rationals x and y, there exists another number z such that z is not rational, and x < z < y. Since this can be translated into a first-order logical formula in the relevant formal language, Łoś's theorem implies that *S has the same property. That is, we can define a notion of the hyperrational numbers, which are a subset of the hyperreals, and they have the same first-order properties as the rationals.Consider, however, the Archimedean property
Archimedean property
In abstract algebra and analysis, the Archimedean property, named after the ancient Greek mathematician Archimedes of Syracuse, is a property held by some ordered or normed groups, fields, and other algebraic structures. Roughly speaking, it is the property of having no infinitely large or...
of the reals, which states that there is no real number x such that x > 1, x > 1 +1 , x > 1 + 1 + 1, ... for every inequality in the infinite list. Łoś's theorem does not apply to the Archimedean property, because the Archimedean property cannot be stated in first-order logic. In fact, the Archimedean property is false for the hyperreals, as shown by the construction of the hyperreal number ω above.
Ultralimit
- For the ultraproduct of a sequence of metric spaces, see UltralimitUltralimitIn mathematics, an ultralimit is a geometric construction that assigns to a sequence of metric spaces Xn a limiting metric space. The notion of an ultralimit captures the limiting behavior of finite configurations in the spaces Xn and uses an ultrafilter to avoid the process of repeatedly passing...
.
In model theory
Model theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
and set theory
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
, an ultralimit or limiting ultrapower is a direct limit
Direct limit
In mathematics, a direct limit is a colimit of a "directed family of objects". We will first give the definition for algebraic structures like groups and modules, and then the general definition which can be used in any category.- Algebraic objects :In this section objects are understood to be...
of a sequence of ultrapowers.
Beginning with a structure, A0, and an ultrafilter, D0, form an ultrapower, A1. Then repeat the process to form A2, and so forth. For each n there is a canonical diagonal embedding
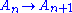. At limit stages, such as Aω, form the direct limit of earlier stages. One may continue into the transfinite.